A vector defined in a [katex] 3 [/katex]-dimensional space. For example,

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Pythagorean theorem

Column vector

Vector notation

Math resources Algebra

Vector

Magnitude of a Vector

Magnitude of a vector

Here you will learn about the magnitude of a vector, including what the magnitude of a vector is and how to calculate it.

Students will first learn about the magnitude of a vector as part of the number system in high school.

What is the magnitude of a vector?

The magnitude of a vector is the length of a vector. The magnitude of the vector $\textbf{a}$ is written as $\lvert \textbf{a} \rvert.$

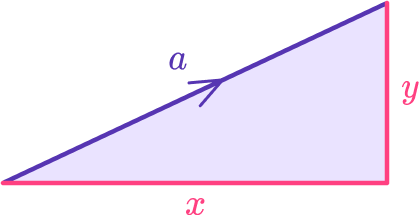
Vector $a$ has two components. There is a horizontal component and a vertical component.

a=\langle x, y\rangle

^vector in component form where $x$ represents the horizontal component and $y$ represents the vertical component.

Below is the magnitude of a vector formula. Notice how it incorporates the pythagorean theorem (or the distance formula).

|\textbf{a}|=\sqrt{x^2+y^2}

If a vector has a magnitude of $1,$ it is a unit vector.

For example,

a=\langle 3,4\rangle

$x=3$ (horizontal component)

$y=4$ (vertical component)

Using the initial point and the terminal point of the vector, the components of the vector make a right triangle. The length of the vector is the hypotenuse of the right triangle.

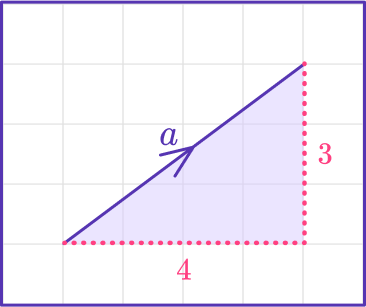
The magnitude of vector $a$ is $\sqrt{4^2+3^2}=\sqrt{25}=5.$

Note: That the answer is the absolute value of the square root of the sum of the vector components, since you are solving for the magnitude not the direction of a vector.

The length of the vector is $5.$

Note: This page covers only $2$ -dimensional vectors.

What is the magnitude of a vector?

Common Core State Standards

How does this relate to high school math?

The Number System (HSN.VM.A.1)
Recognize vector quantities as having both magnitude and direction. Represent vector quantities by directed line segments, and use appropriate symbols for vectors and their magnitudes (e.g., v, |v|, ||v||, v).

[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)

Use this quiz to check your grade 6 – grade 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th to 8th grade algebra topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)

DOWNLOAD FREE

How to calculate the magnitude of a vector

In order to calculate the magnitude of a vector:

Identify the components of the vector.
Calculate the distance.

Magnitude of a vector examples

Example 1: magnitude of a vector – decimal rounded

Find the magnitude of vector $b,$ rounding to the nearest tenth:

b=\langle 5,2\rangle

Identify the components of the vector.

The horizontal component is $x=5$

The vertical component is $y=2$

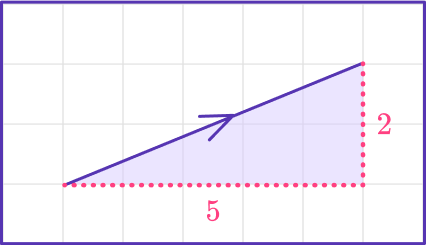
2Calculate the distance.

Use the distance formula:

\sqrt{x^2+y^2}=\sqrt{5^2+2^2}=\sqrt{29}

The magnitude of the vector is $\sqrt{29}=5.3851…=5.4.$

Note: Calculating the magnitude of the vector does not address the direction of the vector.

Example 2: magnitude of a vector – decimal rounded

Find the magnitude of vector $v,$ rounding to the nearest tenth:

v=\langle-1,3\rangle

Identify the components of the vector.

The horizontal component is $x=-1$

The vertical component is $y=3$

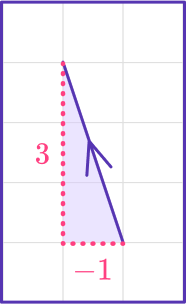
Calculate the distance.

Use the distance formula:

$\sqrt{x^2+y^2}=\sqrt{(-1)^2+3^2}=\sqrt{10}$

The magnitude of the vector is $\sqrt{10}=3.1622…=3.2.$

Example 3: magnitude of a vector – decimal rounded

Find the magnitude of vector $a,$ rounding to the nearest tenth:

a=\langle-4,5\rangle

Identify the components of the vector.

The horizontal component is $x=-4$

The vertical component is $y=5$

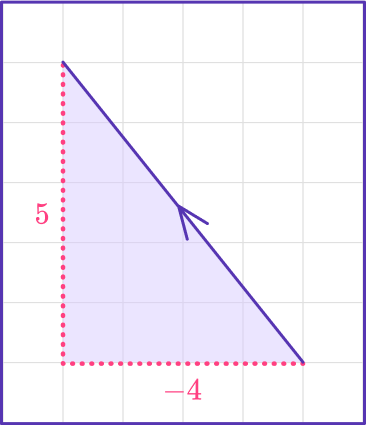
Calculate the distance.

Use the distance formula:

$\sqrt{x^2+y^2}=\sqrt{(-4)^2+5^2}=\sqrt{41}$

The magnitude of the vector is $\sqrt{41}=6.4031…=6.4.$

Example 4: magnitude of a vector – decimal rounded

Find the magnitude of vector $b,$ rounding to the nearest tenth:

b=\langle-2,-3\rangle

Identify the components of the vector.

The horizontal component is $x=-2$

The vertical component is $y=-3$

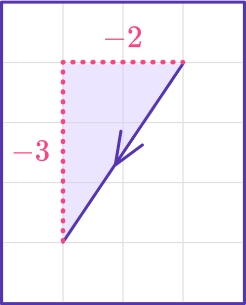
Calculate the distance.

Use the distance formula:

$\sqrt{x^2+y^2}=\sqrt{(-2)^2+(-3)^2}=\sqrt{13}$

The magnitude of the vector is $\sqrt{13}=3.6055…=3.6.$

Example 5: magnitude of a vector – decimal rounded

Find the magnitude of vector $c,$ rounding to the nearest tenth:

c=\langle-4,-6\rangle

Identify the components of the vector.

The horizontal component is $x=-4$

The vertical component is $y=-6$

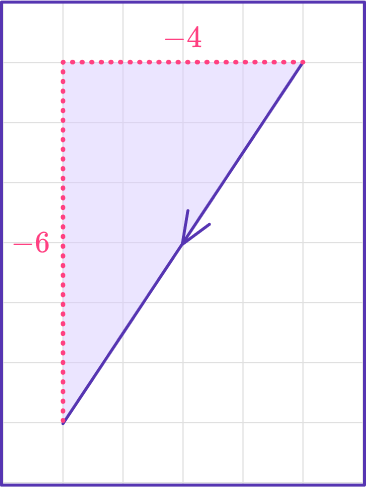
Calculate the distance.

Use the distance formula:

$\sqrt{x^2+y^2}=\sqrt{(-4)^2+(-6)^2}=\sqrt{52}$

The magnitude of the vector is $\sqrt{52}=7.2111…=7.2.$

Example 6: magnitude of a vector – decimal rounded

Find the magnitude of vector $v,$ rounding to the nearest tenth:

v=\langle 2,-7\rangle

Identify the components of the vector.

The horizontal component is $x=2$

The vertical component is $y=-7$

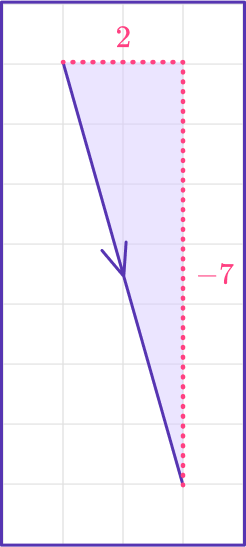
Calculate the distance.

Use the distance formula:

$\sqrt{x^2+y^2}=\sqrt{2^2+(-7)^2}=\sqrt{53}$

The magnitude of the vector is $\sqrt{53}=7.2801…=7.3.$

Teaching tips for magnitude of a vector

Introduce vectors with worksheets that include their position clearly on the $x$ -axis and $y$ -axis. This helps students make connections to previous learning about cartesian coordinates, right triangles and distance.

Have students discover the component form of vectors by having them use the distance formula or online platforms such as Desmos.

Easy mistakes to make

Confusing vectors and scalars
Scalar quantities only involve magnitude, not direction. Vectors involve both.

Confusing vectors and matrices
A vector is a list of numbers that can be in row or column form. It is a special form of a matrix. Anything that has more than $1$ row and/or column is not a vector, it is a matrix.

Making mistakes when squaring negative values
A negative number squared gives a positive answer. If you need to square a negative number using a calculator, it is a good idea to use brackets to make sure that you get the correct answer.

Vector multiplication
Component form of a vector
Subtracting vectors
Adding vectors
Vector practice problems

Practice magnitude of a vector questions

8.6

4.8

4.9

8.5

The magnitude of the vector is $\sqrt{x^2+y^2}=\sqrt{3^2+8^2}=\sqrt{73}=8.544…=8.5$

8.0

5.3

8.1

5.2

The magnitude of the vector is $\sqrt{x^2+y^2}=\sqrt{4^2+7^2}=\sqrt{65}=8.062…=8.1$

3.2

3.1

1.7

1.8

The magnitude of the vector is $\sqrt{x^2+y^2}=\sqrt{1^2+(-3)^2}=\sqrt{10}=3.162…=3.2$

4.4

5.1

5.2

4.5

The magnitude of the vector is $\sqrt{x^2+y^2}=\sqrt{2^2+(-4)^2}=\sqrt{20}=4.472…=4.5$

3.7

3.6

2.4

2.5

The magnitude of the vector is $\sqrt{x^2+y^2}=\sqrt{(-3)^2+2^2}=\sqrt{13}=3.605…=3.6$

4.2

5.1

4.1

5.2

The magnitude of the vector is $\sqrt{x^2+y^2}=\sqrt{(-1)^2+(-4)^2}=\sqrt{17}=4.123…=4.1$

Magnitude of a vector FAQs

What is a 3D vector?

A vector defined in a $3$ -dimensional space. For example,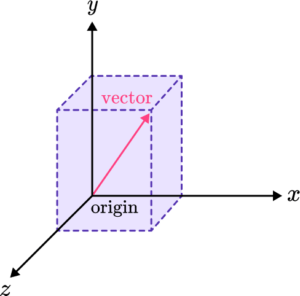

Magnitude of a vector 9 US

What is the component form of a vector?

The component form shows the change in $x$ and $y$ that occur in the vector between endpoints. To write a vector in component form, find the change in $x$ and then the change in $y.$

What is a resultant vector?

Is the answer to a vector addition problem, or the sum of at least two vectors.

Can you multiply a vector by a vector?

Yes, the magnitude of a vector can be used to calculate the dot product of two vectors. It is also possible to calculate the cross product of two vectors.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.