Subtracting Vectors - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Addition and subtraction Negative numbers

Vector notation

Column vectors

Adding vectors

Math resources Algebra

Vectors

Subtracting vectors

Here you will learn about vector subtraction, including representing subtracting vectors graphically and understanding the subtraction of vectors as magnitude.

Students will first learn about the subtraction of vectors as a part of Vector and Matrix Quantities in high school mathematics.

What is vector subtraction?

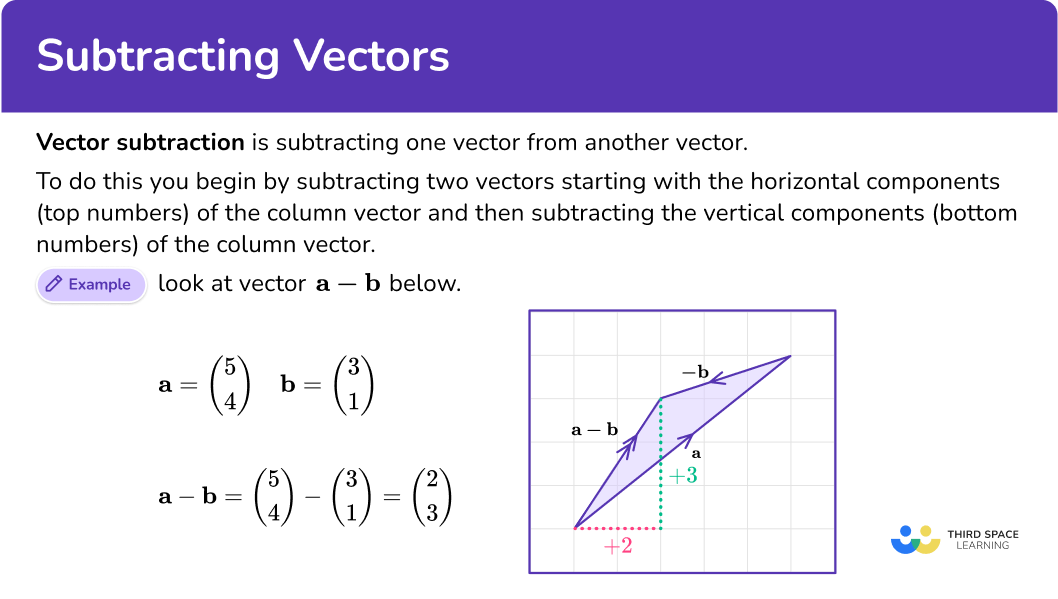
Vector subtraction is subtracting one vector from another vector.

To do this, subtract the horizontal components (top numbers) of the column vector and subtract the vertical components (bottom numbers) of the column vector.

For example, look at vector $\mathbf{a}$ and vector $\mathbf{b}.$

\mathbf{a}= \left(\begin{aligned} 5\\ 4\\ \end{aligned}\right) \quad \mathbf{b}= \left(\begin{aligned} 3\\ 1\\ \end{aligned}\right)

\mathbf{a}-\mathbf{b}= \left(\begin{aligned} 5\\ 4\\ \end{aligned}\right) -\ \left(\begin{aligned} 3\\ 1\\ \end{aligned}\right) =\ \left(\begin{aligned} 2\\ 3\\ \end{aligned}\right)

Subtracting vectors is based on the addition of vectors. The first vector stays the same, but the second vector reverses to the opposite direction to become a negative vector. Using the inverse allows you to change vector subtraction to vector addition.

\mathbf{a}-\mathbf{b}=\mathbf{a}+-\mathbf{b}

Using vector $\mathbf{a}$ and vector $\mathbf{b},$ let’s see what happens.

\mathbf{a}= \left(\begin{aligned} 5\\ 4\\ \end{aligned}\right)

\mathbf{b}= \left(\begin{aligned} 3\\ 1\\ \end{aligned}\right)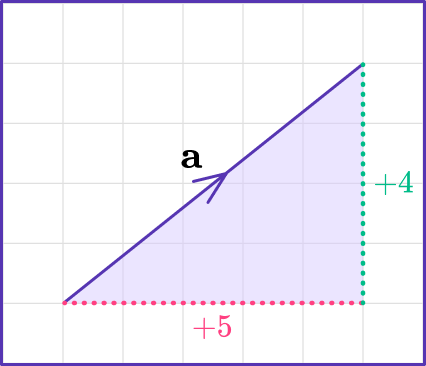

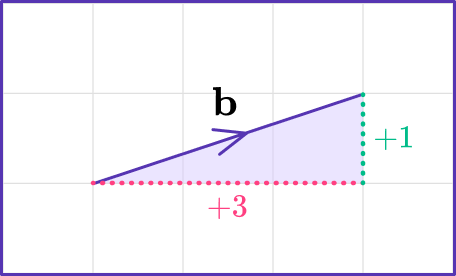
The direction of the vector $\mathbf{-b}$ is opposite to the direction of the original vector $\mathbf{b},$ but has the same magnitude of the resultant vector, or distance from the initial point or starting point.

-\mathbf{b}= \left(\begin{aligned} -3\\ -1\\ \end{aligned}\right)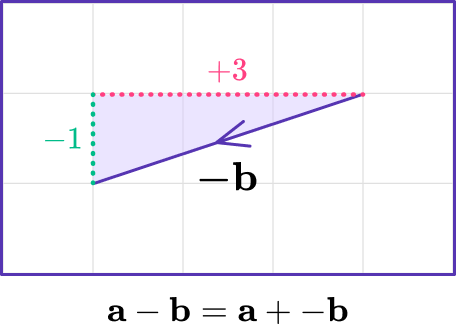

You know from vector addition that when adding two vectors, you add the second on to the end of the first, as shown below.

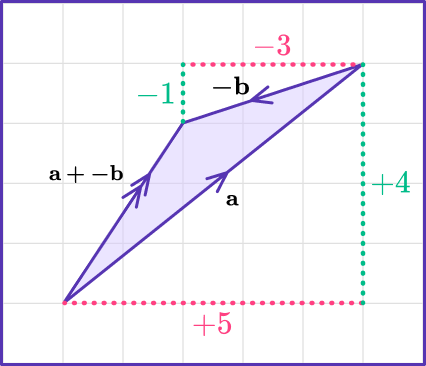
The final answer is known as the resultant vector or new vector.

\mathbf{a}-\mathbf{b}=\textbf{a}+ -\textbf{b}= \left(\begin{aligned} 5\\ 4\\ \end{aligned}\right) +\ \left(\begin{aligned} -3\\ -1\\ \end{aligned}\right) =\ \left(\begin{aligned} 2\\ 3\\ \end{aligned}\right)

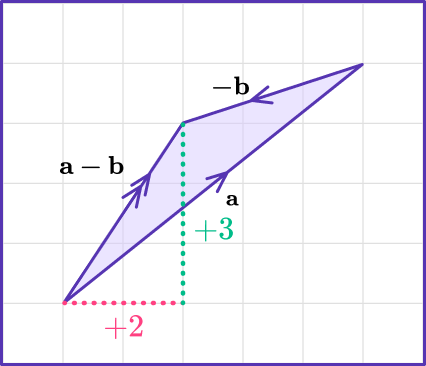
Therefore,

\mathbf{a}-\mathbf{b}= \left(\begin{aligned} 5\\ 4\\ \end{aligned}\right) -\ \left(\begin{aligned} 3\\ 1\\ \end{aligned}\right) =\ \left(\begin{aligned} 2\\ 3\\ \end{aligned}\right)

What is vector subtraction?

Common Core State Standards

How does this relate to high school math?

High School: Number and Quantity: Vector and Matrix Quantities (HSN.VM.B.4)
Understand vector subtraction $v-w$ as $v + (-w),$ where $-w$ is the additive inverse of $w,$ with the same magnitude as $w$ and pointing in the opposite direction. Represent vector subtraction graphically by connecting the tips in the appropriate order, and perform vector subtraction component-wise.

[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)

Use this quiz to check your grade 6 – grade 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th to 8th grade algebra topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)

DOWNLOAD FREE

How to subtract vectors

In order to subtract a vector from an original vector:

Subtract the $\textbf{x}$ components.
Subtract the $\textbf{y}$ components.
Write the resultant vector.

Vector subtraction examples

Example 1: subtract vectors

Subtract the vectors below.

\left(\begin{aligned} 6\\ 4\\ \end{aligned}\right) -\ \left(\begin{aligned} 4\\ 3\\ \end{aligned}\right)

Subtract the $\textbf{x}$ components.

Subtract the second top number from the first top number.

6-4=2

2Subtract the $\textbf{y}$ components.

Subtract the second bottom number from the first bottom number.

4-3=1

3Write the resultant vector.

Write the two answers as a column vector.

\left(\begin{aligned} 6\\ 4\\ \end{aligned}\right) -\ \left(\begin{aligned} 4\\ 3\\ \end{aligned}\right) =\ \left(\begin{aligned} 2\\ 1\\ \end{aligned}\right)

Example 2: subtract vectors

Solve.

\left(\begin{aligned} 3\\ 2\\ \end{aligned}\right) -\ \left(\begin{aligned} 5\\ 1\\ \end{aligned}\right)

Subtract the $\textbf{x}$ components.

Subtract the second top number from the first top number.

$3-5=-2$

Subtract the $\textbf{y}$ components.

Subtract the second bottom number from the first bottom number.

$2-1=1$

Write the resultant vector.

Write the two answers as a column vector.

$\left(\begin{aligned} 3\\ 2\\ \end{aligned}\right) -\ \left(\begin{aligned} 5\\ 1\\ \end{aligned}\right) =\ \left(\begin{aligned} -2\\ 1\\ \end{aligned}\right)$

Example 3: subtract vectors

Solve.

\left(\begin{aligned} 2\\ 4\\ \end{aligned}\right) -\ \left(\begin{aligned} 2\\ 6\\ \end{aligned}\right)

Subtract the $\textbf{x}$ components.

Subtract the second top number from the first top number.

$2-2=0$

Subtract the $\textbf{y}$ components.

Subtract the second bottom number from the first bottom number.

$4-6= -2$

Write the resultant vector.

Write the two answers as a column vector.

\left(\begin{aligned} 2\\ 4\\ \end{aligned}\right) -\ \left(\begin{aligned} 2\\ 6\\ \end{aligned}\right) =\ \left(\begin{aligned} 0\\ -2\\ \end{aligned}\right)

Example 4: subtract vectors

Solve.

\left(\begin{aligned} -4\\ 3\\ \end{aligned}\right) -\ \left(\begin{aligned} 2\\ 1\\ \end{aligned}\right)

Subtract the $\textbf{x}$ components.

Subtract the second top number from the first top number.

$-4-2=-6$

Subtract the $\textbf{y}$ components.

Subtract the second bottom number from the first bottom number.

$3-1=2$

Write the resultant vector.

Write the two answers as a column vector.

$\left(\begin{aligned} -4\\ 3\\ \end{aligned}\right) -\ \left(\begin{aligned} 2\\ 1\\ \end{aligned}\right) =\ \left(\begin{aligned} -6\\ 2\\ \end{aligned}\right)$

Example 5: subtract vectors

Solve.

\left(\begin{aligned} -5\\ 2\\ \end{aligned}\right) -\ \left(\begin{aligned} -3\\ -2\\ \end{aligned}\right)

Subtract the $\textbf{x}$ components.

Subtract the second top number from the first top number.

$-5-(-3)=-2$

Subtract the $\textbf{y}$ components.

Subtract the second bottom number from the first bottom number.

$2-(-2)=4$

Write the resultant vector.

Write the two answers as a column vector.

$\left(\begin{aligned} -5\\ 2\\ \end{aligned}\right) -\ \left(\begin{aligned} -3\\ -2\\ \end{aligned}\right) =\ \left(\begin{aligned} -2\\ 4\\ \end{aligned}\right)$

Example 6: subtract vectors

Solve.

\left(\begin{aligned} 2\\ -1\\ \end{aligned}\right) -\ \left(\begin{aligned} -4\\ -3\\ \end{aligned}\right)

Subtract the $\textbf{x}$ components.

Subtract the second top number from the first top number.

$2--4=6$

Subtract the $\textbf{y}$ components.

Subtract the second bottom number from the first bottom number.

$-1--3=2$

Write the resultant vector.

Write the two answers as a column vector.

\left(\begin{aligned} 2\\ -1\\ \end{aligned}\right) -\ \left(\begin{aligned} -4\\ -3\\ \end{aligned}\right) =\ \left(\begin{aligned} 6\\ 2\\ \end{aligned}\right)

Teaching tips for subtracting vectors

Encourage students to visualize vector subtraction using diagrams or geometric representations. This helps them understand the concept of subtracting one vector from another, considering both magnitude and direction of the arrowhead.

Drawing vectors on a coordinate system can aid in visualizing the process. Have students draw the $x$ -axis and $y$ -axis and utilize prior knowledge to help them visualize the components of vectors.

Teach the head-to-tail method for vector subtraction. In this method, place the tail of the second vector at the head of the first vector, and the resulting vector goes from the tail of the first vector to the head of the second vector. Emphasize the importance of maintaining the order of subtraction for accurate results, as the commutative property does not apply to vector subtraction.

Break down vectors into their components (horizontal and vertical) and teach students to subtract corresponding components separately. This method is particularly useful when working with vectors in two-dimensional space. After subtracting components, guide students to combine the results to obtain the resultant vector.

Provide real-world examples and word problems that involve vector subtraction. This helps students connect the mathematical concept to practical scenarios. Use scenarios such as a displacement vector, velocity, or force vectors to make the learning experience more engaging and applicable.

Draw on student knowledge of trigonometry, the pythagorean theorem and geometric figures like parallelograms to help their understanding.

Easy mistakes to make

Ignoring direction
One common mistake is neglecting the directional aspect of vectors. Students may focus solely on the magnitudes and forget that vectors have both magnitude and direction. Emphasize the importance of the direction of the resultant when subtracting vectors to avoid this error.

Confusing head-to-tail order
In the head-to-tail method, the order of subtraction matters. Prompt students to recall that subtraction is not commutative. Students might inadvertently reverse the order of vectors, leading to incorrect results. Remind them to maintain the correct order to ensure accurate vector subtraction.

Component confusion
Misunderstanding vector components is another common mistake. Students might confuse horizontal and vertical components or mix up the signs when subtracting. Reinforce the concept of breaking down vectors into components and subtracting them separately to minimize this error.

Forgetting negative vectors
Since vector subtraction is equivalent to adding the negative of a vector, students may forget to include the negative sign when subtracting. Remind them to pay attention to signs and clarify the connection between subtraction and the addition of negative vectors.

Skipping visualization
Students may skip the visualization step and attempt to subtract vectors algebraically without understanding the geometric representation using the coordinate system. Encourage them to draw diagrams or use graphical aids to visualize the initial endpoint, the length of the arrow, and the magnitude of a vector, helping to prevent errors related to misinterpretation.

Vector multiplication
Component form of a vector
Vector practice problems
Magnitude of a vector

Practice vector subtraction questions

\left(\begin{aligned} -3\\ 2\\ \end{aligned}\right)

\left(\begin{aligned} 3\\ 2\\ \end{aligned}\right)

\left(\begin{aligned} -3\\ -2\\ \end{aligned}\right)

\left(\begin{aligned} 3\\ -2\\ \end{aligned}\right)

\textbf{v}-\textbf{w}=\left(\begin{aligned} 7\\ 3\\ \end{aligned}\right) -\ \left(\begin{aligned} 4\\ 1\\ \end{aligned}\right) =\ \left(\begin{aligned} 3\\ 2\\ \end{aligned}\right)

\left(\begin{aligned} -3\\ -5\\ \end{aligned}\right)

\left(\begin{aligned} -3\\ 5\\ \end{aligned}\right)

\left(\begin{aligned} 3\\ 5\\ \end{aligned}\right)

\left(\begin{aligned} 3\\ -5\\ \end{aligned}\right)

\textbf{c}-\textbf{d}=\left(\begin{aligned} 6\\ 2\\ \end{aligned}\right) -\ \left(\begin{aligned} 3\\ 7\\ \end{aligned}\right) =\ \left(\begin{aligned} 3\\ -5\\ \end{aligned}\right)

\left(\begin{aligned} 6\\ 2\\ \end{aligned}\right)

\left(\begin{aligned} -6\\ -2\\ \end{aligned}\right)

\left(\begin{aligned} 6\\ -2\\ \end{aligned}\right)

\left(\begin{aligned} -6\\ 2\\ \end{aligned}\right)

\textbf{b}-\textbf{a}=\left(\begin{aligned} 5\\ 4\\ \end{aligned}\right) -\ \left(\begin{aligned} -1\\ 6\\ \end{aligned}\right) =\ \left(\begin{aligned} 6\\ -2\\ \end{aligned}\right)

\left(\begin{aligned} -1\\ -2\\ \end{aligned}\right)

\left(\begin{aligned} 1\\ -2\\ \end{aligned}\right)

\left(\begin{aligned} 1\\ 2\\ \end{aligned}\right)

\left(\begin{aligned} -1\\ 2\\ \end{aligned}\right)

\textbf{p}-\textbf{q}=\left(\begin{aligned} -3\\ 6\\ \end{aligned}\right) -\ \left(\begin{aligned} -2\\ 4\\ \end{aligned}\right) =\ \left(\begin{aligned} -1\\ 2\\ \end{aligned}\right)

\left(\begin{aligned} -5\\ 6\\ \end{aligned}\right)

\left(\begin{aligned} -5\\ -6\\ \end{aligned}\right)

\left(\begin{aligned} 5\\ 6\\ \end{aligned}\right)

\left(\begin{aligned} 5\\ -6\\ \end{aligned}\right)

\textbf{s}-\textbf{r}=\left(\begin{aligned} -2\\ -1\\ \end{aligned}\right) -\ \left(\begin{aligned} 3\\ 5\\ \end{aligned}\right) =\ \left(\begin{aligned} -5\\ -6\\ \end{aligned}\right)

\left(\begin{aligned} 2\\ -3\\ \end{aligned}\right)

\left(\begin{aligned} 2\\ 3\\ \end{aligned}\right)

\left(\begin{aligned} -2\\ 3\\ \end{aligned}\right)

\left(\begin{aligned} -2\\ -3\\ \end{aligned}\right)

\textbf{e}-\textbf{d}=\left(\begin{aligned} -4\\ 3\\ \end{aligned}\right) -\ \left(\begin{aligned} -2\\ 6\\ \end{aligned}\right) =\ \left(\begin{aligned} -2\\ -3\\ \end{aligned}\right)

Subtracting vectors FAQs

How do you subtract vectors using the head-to-tail method?

Vector subtraction using the head-to-tail method involves placing the tail of the second vector at the head of the first vector. The resultant vector then goes from the tail of the first vector to the head of the second vector. It’s crucial to maintain the correct order to ensure precise results in vector operations.

What are the most common mistakes to avoid when subtracting vectors?

Common mistakes in vector subtraction include neglecting vector direction, confusing the head-to-tail order, misunderstanding vector components, and forgetting to account for negative vectors. Visualization and careful attention to these aspects help prevent errors and ensure accurate results in vector mathematics.

Can vector subtraction be simplified by breaking it into components?

Yes, vector subtraction can be simplified by breaking it into components. By decomposing vectors into horizontal and vertical components, students can subtract corresponding components separately. This method aids in clarity and accuracy when performing vector subtraction in two-dimensional space.

How does negative vector addition relate to vector subtraction?

Vector subtraction is equivalent to adding the negative of a vector. When subtracting a vector, you can achieve the same result by adding its negative and finding the vector sum. Paying attention to signs and understanding this relationship simplifies vector operations and provides a conceptual bridge between vector addition and subtraction.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.