High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Rate of change formula How to find the slope of a line Parallel linesComponent form of a vector
Here you will learn about the component form of a vector, how to write a vector in component form including the meaning of the component form of a vector and how to use it to solve problems.
Students first learn about vectors in high school in a geometry class when they learn about translations and expand their knowledge as they progress through precalculus and calculus.
What is the component form of a vector?
The component form of a vector is the ordered pair of a vector that describes the movement or the change in the x and y values.
It is a way to represent a vector using ordered pairs, where the first value ( x -component) represents the horizontal movement or horizontal displacement and the second value ( y -component) represents the vertical movement or vertical displacement of the vector.
Vector \vec{v} which is pictured below.
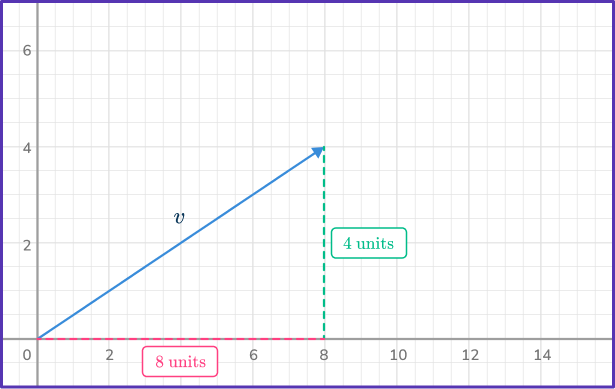
Vector \vec{v} can be written in component form as \vec{v}=\langle{8, \, 4}\rangle.
Notice how the x -component is 8 and the y -component is 4.
This is because from the initial point of the vector to the terminal point (or endpoint) of the vector, there is a horizontal movement of 8 units right and a vertical movement that is 4 units up.
Let’s look at how to calculate the component form of a vector.
Vector \vec{AB} has an initial point of (- \, 4, \, 3) and a terminal point of (- \, 1, \, 7). Write vector \vec{AB} in component form.
First, let’s look at the points on the coordinate plane.
Notice how from the initial point to the terminal point there is a horizontal movement of 3 units right and then a vertical movement of 4 units up.
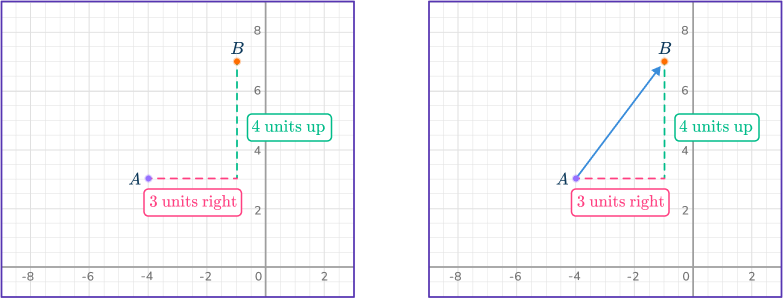
The component form of vector \vec{AB} is \langle{3, \, 4}\rangle.
Another way to calculate the component form of a vector is to use the formula.
Component form of a vector: \langle{x_2-x_1, \, y_2-y_1}\rangle
Notice how the x -component represents the change in the x -coordinates, and the y -coordinate represents the change in the y -coordinates.
That is exactly what you did when you determined the x -component and y -component on the graph.
Let’s use the formula to calculate the component form of vector \vec{AB}.
In this case, the initial point of vector \vec{AB} is A \, (- \, 4, \, 3) and the terminal point is B \, (- \, 1, \, 7).
Initial point: \left(x_1, \, y_1\right)=A \, (- \, 4, \, 3)
Terminal point: \left(x_2, \, y_2\right)=B \, (- \, 1, \, 7)
Component form of vector \vec{AB}=\langle{- \, 1-(- \, 4), \, 7-3}\rangle \rightarrow \langle{3, \, 4}\rangle
Notice how the notation of the component form has v -shaped parentheses.
![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Algebra Worksheet (Grade 6 to 8)
![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
Teaching component form of a vector? Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of algebra topics to identify areas of strength and support!
DOWNLOAD FREE NOW![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Algebra Worksheet (Grade 6 to 8)
![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
Teaching component form of a vector? Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of algebra topics to identify areas of strength and support!
DOWNLOAD FREE NOWParallel vectors
Vectors are considered to be parallel if they point in the same direction or exactly in opposite directions. Let’s look at two vectors that are in component form.
Vector \vec{v}=\langle{- \, 5, \, 1}\rangle
Vector \vec{w}=\langle{5, \, - \, 1}\rangle
You know that lines are parallel if they have the same slope. It’s not much different for vectors. In component form, the x -component is the change in x and the y -component is the change in y.
So, looking at vector \vec{v}, the slope is \cfrac{1}{- \, 5} and looking at vector \vec{w}, the slope is \cfrac{- \, 1}{5}.
Now, let’s look at the vectors on the graph.
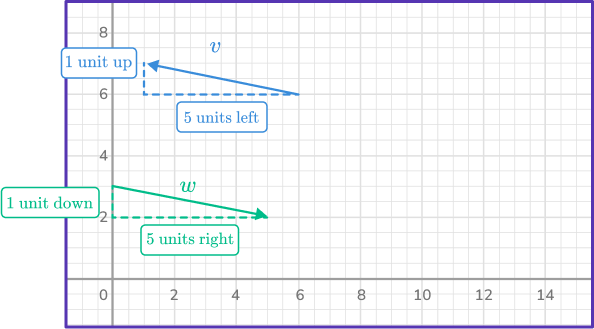
You can see that the vectors are parallel even though they are pointing in exactly opposite directions.
Vector \vec{v} and vector \vec{w} are also considered negative vectors because they are parallel and point in exactly opposite directions, \vec{v}=- \, \vec{w}.
What is the component form of a vector?

Common Core State Standards
How does this relate to high school math?
- High School – The Real Number System – Vector and Matrix Quantities: HSN-VM.A.2 (+)
Find the components of a vector by subtracting the coordinates of an initial point from the coordinates of a terminal point..
How to write a vector in component form from the graph
In order to write a vector in component form from a graph:
- Count the units horizontally from the initial point to the terminal point.
- Count the units vertically from the initial point to the terminal point.
- Write the vector in component form.
Vector in component form examples
Example 1: vector on a graph
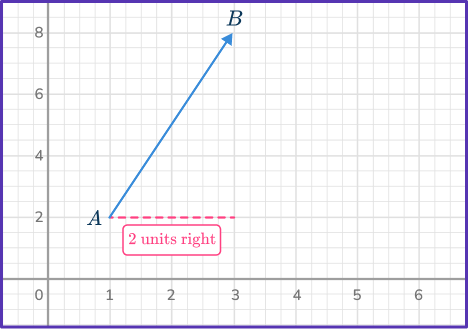
Write the component form of vector \vec{AB}.
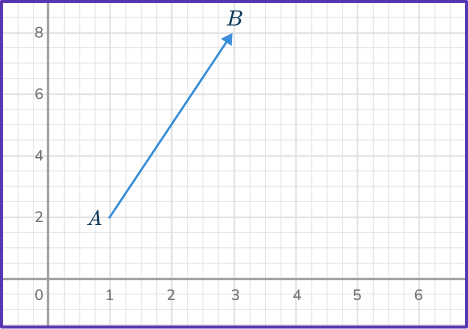
- Count the units horizontally from the initial point to the terminal point.
2Count the units vertically from the initial point to the terminal point.
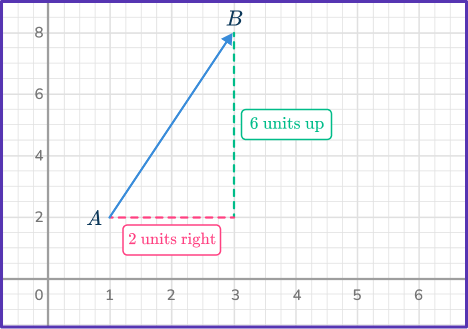
3Write the vector in component form.
Since there are two units right, the x -component is 2, and since there are 6 units up, the y -component is 6.
Vector \vec{AB}=\langle{2, \, 6}\rangle.
Example 2: vector on a graph
Write the component form of vector \vec{CD}.
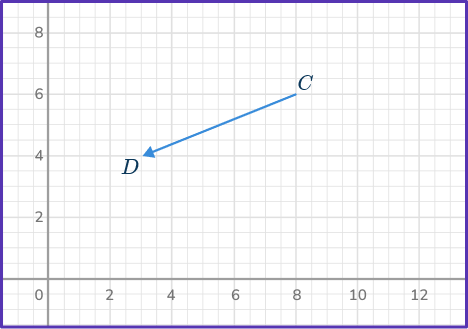
Count the units horizontally from the initial point to the terminal point.
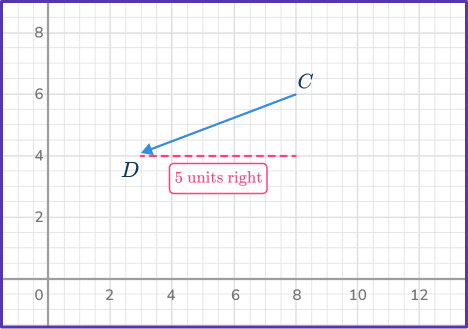
Count the units vertically from the initial point to the terminal point.
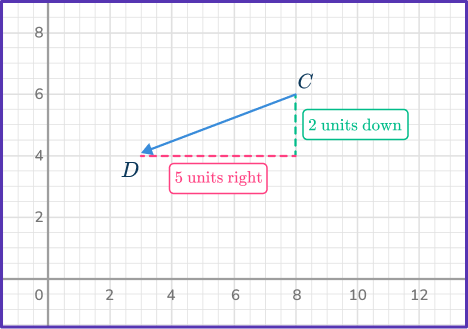
Write the vector in component form.
Since there are five units right, the x -component is 5, and since there are 2 units down, the y -component is - \, 2.
Vector \vec{CD}=\langle{5, \, - \, 2}\rangle
How to write a vector in component form using the formula
In order to write a vector in component form using the formula:
- Identify \bf{\left(\textbf{x}_1, \, \textbf{y}_1\right)} and \bf{\left(\textbf{x}_2, \, \textbf{y}_2\right)}.
- Calculate the component form.
- Write the vector in component form.
Example 3: calculate component form
Vector \vec{AB} has an initial point A \, (- \, 3, \, 7) and a terminal point B \, (- \, 1, \, - \, 1). Write the vector in component form.
Identify \bf{\left(\textbf{x}_1, \, \textbf{y}_1\right)} and \bf{\left(\textbf{x}_2, \, \textbf{y}_2\right)}.
The initial point A \, (- \, 3, \, 7) is \left(x_1, \, y_1\right).
The terminal point B \, (- \, 1, \, - \, 1) is \left(x_2, \, y_2\right).
Calculate the component form.
Component form of a vector: \langle{x_2-x_1, \, y_2-y_1}\rangle
Component form of vector \vec{AB}=\langle{- \, 1-(- \, 3), \, - \, 1-7}\rangle=\langle{2, \, - \, 8}\rangle
Write the vector in component form.
Component form of \vec{AB}=\langle{2, \, - \, 8}\rangle.
Example 4: calculate component form
Vector \vec{v} has an initial point (0, \, 6) and a terminal point (10, \, - \, 1).
Write the vector in component form.
Identify \bf{\left(\textbf{x}_1, \, \textbf{y}_1\right)} and \bf{\left(\textbf{x}_2, \, \textbf{y}_2\right)}.
The initial point of vector \vec{v}, \, (0, \, 6)=\left(x_1, \, y_1\right).
The terminal point of vector \vec{v}, \, (10, \, - \, 1)=\left(x_2, \, y_2\right).
Calculate the component form.
Component form of the vector: \langle{x_2-x_1, \, y_2-y_1}\rangle
Component form of vector \vec{v}=\langle{10-0, \, - \, 1-6}\rangle=\langle{10, \, - \,7}\rangle
Write the vector in component form.
Component form of \vec{v}=\langle{10, \, - \, 7}\rangle
How to find terminal or initial point of a vector
In order to find the terminal or initial point of a vector:
- Identify the given information.
- Use \bf{\langle{\textbf{x}_2-\textbf{x}_1, \, \textbf{y}_2-\textbf{y}_1}\rangle} to find the missing point.
- Write the point.
Example 5: find terminal point
Vector \vec{w} in component form is \langle{- \, 9, \, 5}\rangle and has an initial point of (9, \, - \, 4).
Find the terminal point.
Identify the given information.
Vector \vec{w} in component form is \langle{- \, 9, \, 5}\rangle and has an initial point of (9, \, - \, 4) which means that x_1=9 and y_1=- \, 4.
\left(x_2, y_2\right) represents the terminal point.
Use \bf{\langle{\textbf{x}_2-\textbf{x}_1, \, \textbf{y}_2-\textbf{y}_1}\rangle} to find the missing point.
In this case, x_2 and y_2 is what you will be solving for.
The x -component of a vector is equal to x_2-x_1.
The y -component of the vector is y_2-y_1.
Substitute in the values that are given to find the coordinates of the terminal point.
x -value:
\begin{aligned}& - \, 9=x_2-9 \\\\
& - \, 18=x_2 \end{aligned}
y -value:
\begin{aligned}& 5=y_2-(- \, 4) \\\\ & 5=y_2+4 \\\\& 1=y_2 \end{aligned}
Write the point.
The terminal point of vector \vec{w}=(- \, 18, \, 1).
Example 6: find initial point
Vector \vec{u} in component form is \langle{- \, 6, \, - \, 3}\rangle and has a terminal point (- \, 10, \, - \, 10).
Find the initial point of vector \vec{u} .
Identify the given information.
Vector \vec{u} in component form is \langle{- \, 6, \, - \, 3}\rangle and the terminal point is (- \, 10, \, - \, 10) which means you are given (x_2, \, y_2).
Use \bf{\langle{\textbf{x}_2-\textbf{x}_1, \, \textbf{y}_2-\textbf{y}_1}\rangle} to find the missing point.
Since you need to find the initial point of vector \vec{u}, you are solving for (x_1, \, y_1).
The x -component of a vector is equal to x_2-x_1.
The y -component of the vector is y_2-y_1.
Substitute in the values that are given to find the coordinates of the terminal point.
x -value:
\begin{aligned}& - \, 6=- \, 10-x_1 \\\\
& 4=- \, x_1 \\\\
& - \, 4=x_1 \end{aligned}
y -value:
\begin{aligned}& - \, 3=- \, 10-y_1 \\\\
& 7=- \, y_1 \\\\
& - \, 7=y_1 \end{aligned}
Write the point.
The initial point of vector \vec{u} is (- \, 4, \, - \, 7).
Teaching tips for component form of a vector
- Have students discover component form by providing them with graphing activities where they can use the initial point and terminal point of a vector to determine its slope and then component form.
- Incorporate investigative activities on digital graphing platforms.
- Have struggling students use digital platforms that have embedded tutorial videos.
- Instead of worksheets, have students game play to practice skills and concepts.
Easy mistakes to make
- Mixing up the \textbf{x} -component and \textbf{y} -component
When writing a vector in component form, like ordered pairs, write the horizontal movement first ( x -component) and vertical movement second ( y -component).
- Confusing the terminal point with the initial point
For example, when writing the vector \vec{AB} with initial point (8, \, 2) and terminal point (- \, 5, \, 3) in component form, calculating it incorrectly.
\langle{8-(- \, 5), \, 2-3}\rangle=\langle{13, \, - \, 1}\rangle, instead of subtracting the initial point from the terminal point. The correct way to calculate is \langle{- \, 5-8, \, 3-2}\rangle=\langle{- \, 13, \, 1}\rangle.
Unlike finding slope, the order of \langle{x_{2}-x_{1}, \, y_{2}-y_{1}}\rangle is essential to the representation of the vector.
From the graph below, you can see how the vectors are parallel but they are not the same. Further confirming that the order of subtraction is essential to the correct component form of a vector.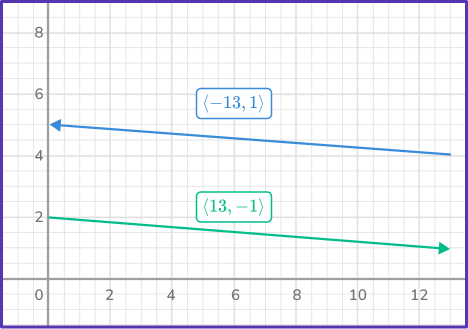
- Thinking that vectors pointing in different directions are not parallel
Vectors are parallel as long as their slopes are the same. They do not have to be pointing in the same direction to be parallel.
- Forgetting to use the \textbf{"v"} shaped brackets
The component form of a vector is not an ordered pair, it represents the horizontal and vertical movement so using the “v” shaped brackets indicates it is not an ordered pair.
Related vector lessons
- Subtracting vectors
- Adding vectors
- Vector multiplication
- Magnitude of a vector
- Vector practice problems
Practice problems for component form of a vector
1. Write the vector \vec{BO} in component form.
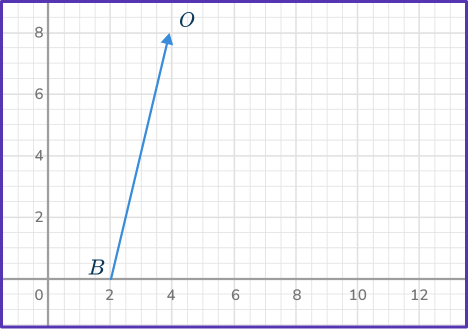




To write the vector in component form, count the number of units horizontally and vertically from the initial point to the terminal point.
2. What is the component form of vector \vec{CD}?
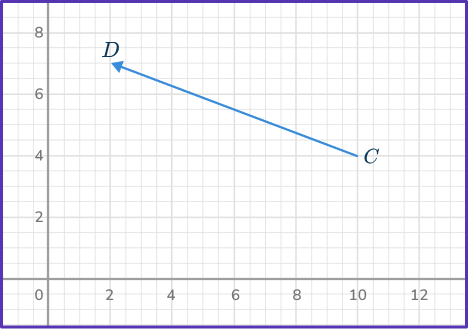




To write the vector in component form, count the number of units horizontally and vertically from the initial point to the terminal point. Be careful about the scale on the x -axis and y- axis as this is not the same as one grid square =1 unit.
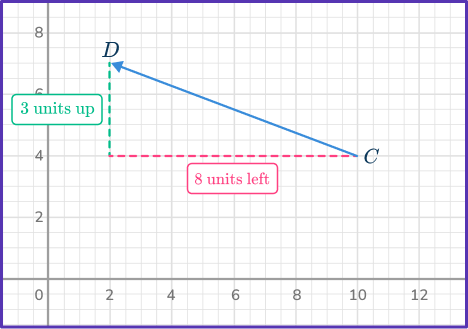
From the initial point to the terminal point there are 8 units left and 3 units up. So, the component form of vector \vec{CD} is \langle{- \, 8, \, 3}\rangle.
3. Vector \vec{v} has an initial point (10, \, – \, 4) and a terminal point (- \, 6, \, 1). What is the component form of vector \vec{v}?




To find the component form of a vector use the formula:
Component form of a vector: \langle{x_2-x_1, \, y_2-y_1}\rangle
The terminal point (- \,6, \, 1) is \left(x_2, \, y_2\right) and the initial point (10, \, – \, 4) is \left(x_1, \, y_1\right).
Substitute the values and make the calculations.
Component form of a vector: \langle{- \, 6-10, \, 1-(- \, 4)}\rangle=\langle{- \, 16, \, 5}\rangle.
The component form of vector \vec{v}=\langle{- \, 16, \, 5}\rangle.
4. Vector \vec{v} has an initial point (9, \, 0) and terminal point (- \, 1, \, – \, 8). Find the component form of vector \vec{v}.




To find the component form of a vector use the formula:
Component form of a vector: \langle{x_2-x_1, \, y_2-y_1}\rangle
The initial point (9, \, 0) is (x_1, \, y_1) and the terminal point (- \, 1, \, – \, 8) is (x_2, \, y_2). Substitute in the values and make the calculation.
\langle{- \, 1-9, \, – \, 8-0}\rangle=\langle{- \, 10, \, – \, 8}\rangle
The component form of vector \vec{v} is \langle{- \, 10, \, – \, 8}\rangle.
5. The component form of vector \vec{w} is <3, \, – \, 11>. If the initial point of vector \vec{w} is (6, \, 7) what is the terminal point?




You are given the component form, \langle{3, \, – \, 11}\rangle and the initial point (6, \, 7) of vector \vec{w}.
Using the formula: \langle{x_2-x_1, \, y_2-y_1}\rangle where the initial point is \left(x_1, \, y_1\right) and the x -component =x_2-x_1 and the y -component =y_2-y_1, substitute in the known values to find the terminal point.
Here, 3=x_2-6 and – \, 11=y_2-7, solve them both for the unknown value.
\begin{aligned}3&=x_2-6 \\\\ 9&=x_2 \end{aligned}
\begin{aligned}- \, 11&=y_2-7 \\\\ – \, 4&=y_2 \end{aligned}
The terminal point of vector \vec{w} is (9, \, – \, 4).
6. The component form of vector \vec{AB} is \langle{- \, 2, \, – \, 5}\rangle. If the terminal point of vector \vec{AB} is (1, \, – \, 8), what is the initial point?




You are given the component form, \langle{- \, 2, \, – \, 5}\rangle and the terminal point (1, \, – \, 8) of vector \vec{AB}.
Use the formula: \langle{x_2-x_1, y_2-y_1}\rangle where the terminal point is (x_2, \, y_2) and the x -component =x_2-x_1 and the y -component =y_2-y_1.
Substitute in the known values to find the initial point, – \, 2=1-x_1 and – \, 5=-8-y_1, and solve them both for the unknown value.
\begin{aligned}- \, 2&=1-x_1 \\\\ – \, 3&=-x_1 \\\\ 3&=x_1 \end{aligned}
\begin{aligned}- \, 5&=- \, 8-y_1 \\\\ 3&=- \, y_1 \\\\ – \, 3&=y_1 \end{aligned}
The initial point of vector \vec{AB} is (3, \, – \,3).
Component form of a vector FAQs
Yes, ai+bj is another way of representing a vector where “a’ and “b” are the scalar values representing the x -component (horizontal component) and y -component (vertical component of the vector and “i” and “j” represent the unit vectors.
Another form of writing a vector uses trigonometry in a right triangle where the sine function is used to determine the vertical component of a vector, and the cosine function is used to determine the horizontal component of a vector.
This has practical applications in physics when looking at motion on an incline plane as the motion is on a slope which can be modelled using the hypotenuse of a right triangle.
If you know the angle \theta of the slope, you can calculate the horizontal and vertical components of motion separately using A=H \cos \theta and O=H \sin \theta.
The operations can be applied to vectors such as scalar multiplication, addition and subtraction.
The component form of a vector represents the amount of units horizontally and vertically the initial point is from the terminal point. It represents the change in the x -coordinates and the change in the y -coordinates.
The next lessons are
- Lines
- Angles
- Angles in parallel lines
- Trigonometric identities
- Pythagorean Theorem
- Magnitude of a vector
- Direction of a vector
- Vector addition
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!