High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Coordinate planeNegative numbers
Graphing linear equations Interpreting graphs Plot points on a graphHow to find y intercept
Here you will learn about how to find the y intercept from a straight line graph, including straight lines in the slope intercept form, y=mx+b and standard form, ax+by=c.
Students will first learn about how to find the y intercept in 8 th grade math with their work with linear functions.
What is the y intercept and how do you find the y -intercept?
Finding the y intercept of a straight line is an important skill used to solve algebraic and real-life problems involving straight line graphs.
The intercepts of a graph are where the graph crosses the coordinate axes.
You can find the y intercepts of graphs of all types of functions including straight lines, quadratic functions, cubic functions and others. In this case, the y intercept is the point where the function crosses or intercepts the y -axis.
To find the y intercept(s) of a line:
Substitute x=0 into the equation of the function and evaluate for y.
To find the x intercept(s) of a line:
Substitute y=0 into the equation of the function and evaluate for x.
Note, this is a useful strategy to draw the equation of a straight line.
Step-by-step guide: Graphing Linear Equations
Example
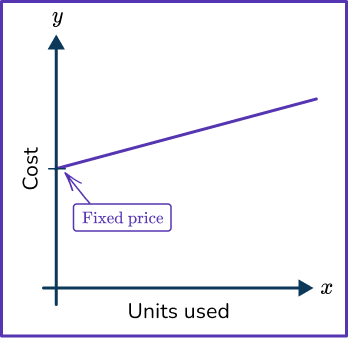
The y intercept of a straight line is the value of y when the x -coordinate is zero.
In this real life example, the y intercept represents the starting value or fixed price, with the slope or gradient representing the unit rate or rate of change.
Let’s look at some examples.
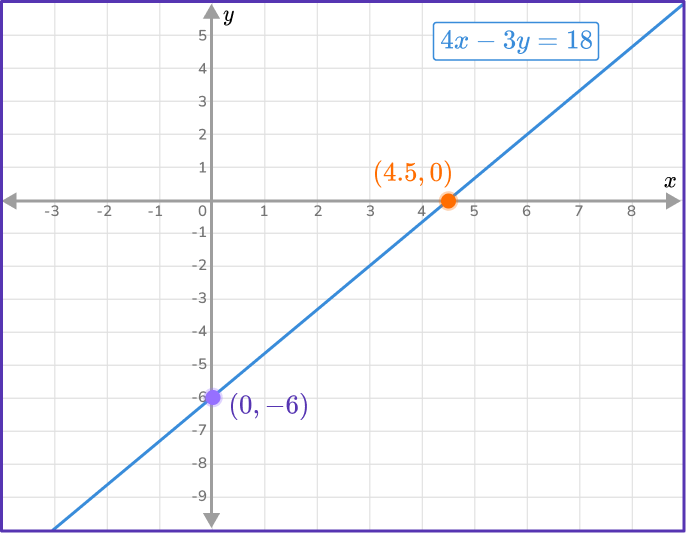
A straight line has the equation, in standard form, 4x-3y=18. Find the y intercept of the line.
To find the y intercept, substitute x=0 into the equation.
4(0)-3y=18Now solve the equation to find the corresponding y value.
\begin{aligned}-3y&=18 \\\\ y&=-6 \end{aligned}The y intercept is -6 and has coordinate (0,-6).
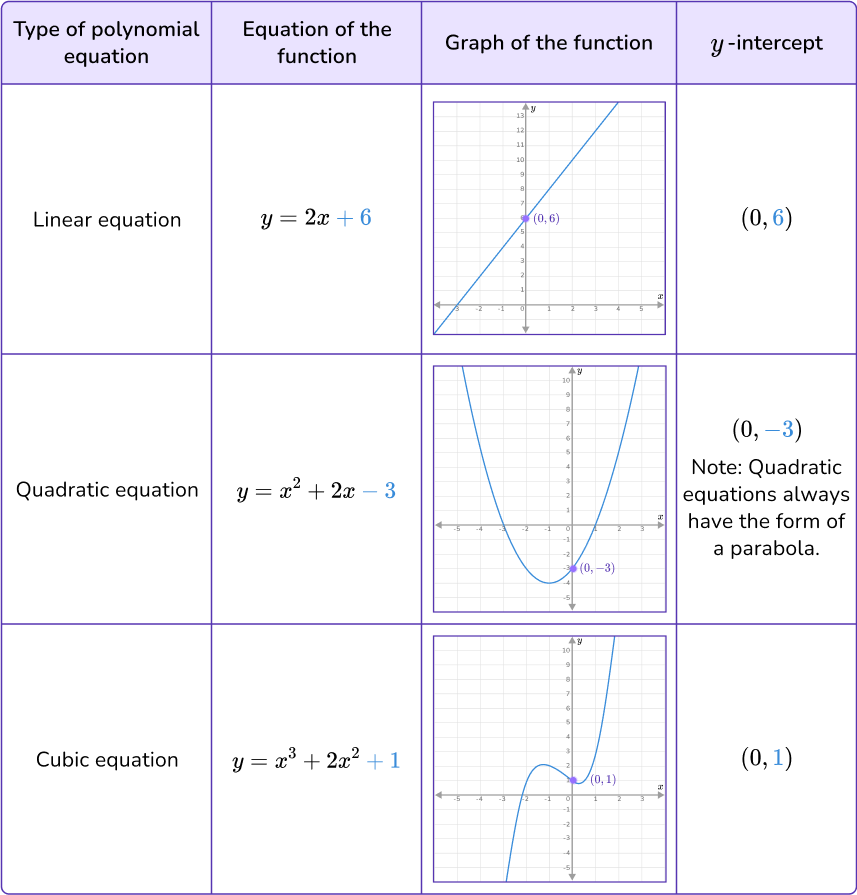
Note: If any function is of the form y=f(x)+\text{constant}, the constant is the y intercept. This is because the y -intercept is always when the x -value is 0, so when substituting 0 for x the constant is going to be the y -value.
See examples of different types of polynomials below.
What is the y intercept and how do you find the y-intercept?
Common Core State Standards
How does this relate to high school math?
- High School: Functions (HS.IF.C.7a)
Graph linear and quadratic functions and show intercepts, maxima, and minima.
![[FREE] How To Find The Y Intercept Worksheet (High School)](https://thirdspacelearning.com/wp-content/uploads/2024/12/How-to-find-the-y-intercept-Worksheet-listing-image.png)
[FREE] How To Find The Y Intercept Worksheet (High School)
![[FREE] How To Find The Y Intercept Worksheet (High School)](https://thirdspacelearning.com/wp-content/uploads/2024/12/How-to-find-the-y-intercept-Worksheet-listing-image.png)
Use this worksheet to check your high school students’ understanding of how to find the y-intercept. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] How To Find The Y Intercept Worksheet (High School)](https://thirdspacelearning.com/wp-content/uploads/2024/12/How-to-find-the-y-intercept-Worksheet-listing-image.png)
[FREE] How To Find The Y Intercept Worksheet (High School)
![[FREE] How To Find The Y Intercept Worksheet (High School)](https://thirdspacelearning.com/wp-content/uploads/2024/12/How-to-find-the-y-intercept-Worksheet-listing-image.png)
Use this worksheet to check your high school students’ understanding of how to find the y-intercept. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEHow to find the y intercept
In order to find the y intercept, you need to:
- Substitute \textbf{x} = \bf{0} into the equation of the line.
- Solve the equation for \textbf{y}.
How to find y intercept examples
Example 1: finding the y intercept of a line in the form y = mx + b
Find the y intercept of the line y=2x-5.
- Substitute \textbf{x} = \bf{0} into the equation of the line.
2Solve the equation for \textbf{y}.
This equation gives y=-5.
The y intercept is -5.
It has coordinates (0,-5).
Note: This is the special case where the equation is in the form y = [function of x ] + \; c (constant). In this case c=-5 so the y intercept is (0,-5).
Example 2: finding the y intercept of a line in the form y = mx + b
Find the y intercept of the line y=\cfrac{1}{2}x+3
Substitute \textbf{x} = \bf{0} into the equation of the line.
Solve the equation for \textbf{y}.
This equation gives y=3.
The y intercept is 3.
It has coordinates (0,3).
Example 3: finding the y intercept of a line in the form y = mx + b
Find the y intercept of the line y=9x-14.
Substitute \textbf{x} = \bf{0} into the equation of the line.
Solve the equation for \textbf{y}.
This equation gives y=-14.
The y intercept is -14.
It has coordinates (0,-14).
Example 4: finding the y intercept of a line in the form ax + by = c
Find the y intercept of the line 2x+5y=20.
Substitute \textbf{x} = \bf{0} into the equation of the line.
Solve the equation for \textbf{y}.
The y intercept is 4.
It has coordinates (0,4).
Example 5: finding the y intercept of a line in the form ax + by = c
Find the y intercept of the line 3x-4y=24.
Substitute \textbf{x} = \bf{0} into the equation of the line.
Solve the equation for \textbf{y}.
The y intercept is -6.
It has coordinates (0,-6).
Example 6: finding the y intercept of a line in the form ax + by = c
Find the y intercept of the line 7x+9y=36.
Substitute \textbf{x} = \bf{0} into the equation of the line.
Solve the equation for \textbf{y}.
The y intercept is 4.
It has coordinates (0,4).
Teaching tips for how to find y intercept
- While introducing the concept of the y -intercept, use multiple visuals where students can clearly see that the y -intercept is the point where the line crosses the y -axis.
- The use of interactive activities, such as online graphing tools or activities that require students to physically graph activities, are just as effective as worksheets with practice problems.
- For students that are struggling, break down the process of finding the y -intercept into simple steps. The use of visuals for each step can aid students in understanding the process.
Easy mistakes to make
- Substituting the wrong value for zero
A common error is to think that the y intercept is when y=0. It is important to remember that when y=0, the line will be crossing the x -axis and therefore will give the x intercept.
- Forgetting to state the coordinates when asked
If an exam question asks for the y intercept or x intercept, just the value where the line crosses the axes is appropriate. However, sometimes the question will ask for the coordinates of the y intercept. In this case the answer must be given in the form (0,b) for the y intercept, or (-\cfrac{b}{m},0) for the coordinates of the x intercept.
- Confusing the intercept with the gradient
When the line is in the form y=mx+b, a common error is to confuse the y intercept, b with the gradient or slope of a line, m. The y intercept will have coordinates (0,b) and the x intercept will have coordinates (-\cfrac{b}{m},0).
Related graphing linear equations lessons
Practice how to find the y intercept questions
1. State the coordinate of the y intercept of the line y=3x-2.




Substitute x=0 to give
\begin{aligned}y&=3(0)-2 \\\\ y&=-2 \end{aligned}
The coordinate of the y -intercept is (0,-2).
2. Find the coordinate of the y intercept of the line y=3x-6.




Substitute x=0 to give
\begin{aligned}y&=3(0)-6 \\ y&=-6 \end{aligned}
The coordinate of the y -intercept is (0,-6).
3. The equation of a line is given as y=8-3x. Find the y intercept.




When x=0,
\begin{aligned}y&=8-3(0) \\\\ y&=8\end{aligned}
4. The equation of a line is given as x-3y=9. Find the y intercept.




When x=0,
\begin{aligned}-3y&=9 \\\\ y&=-3 \end{aligned}
5. The equation of a line is given as 5x-4y=10. Find the y intercept.




When x=0,
\begin{aligned}5(0)-4y&=10 \\\\ -4y&=10 \\\\ y&=-2.5 \end{aligned}
6. The equation of a line is given as -2x+12y=6. Find the y intercept.




When x=0,
\begin{aligned}-2(0)+12y&=6 \\\\ 12y&=6 \\\\ y&=\cfrac{6}{12}=\cfrac{1}{2} \end{aligned}
How to find y intercept FAQs
The process for finding the x -intercept of a line is similar to finding the y -intercept. Instead of substituting x=0, you would substitute y=0, and solve the equation for x.
Yes, the process for finding the y -intercept in point-slope form is similar to any other linear equation. You will substitute x=0 into the equation and then solve for y.
To find the slope of the line, you will use the formula: m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}, where the slope (m), is found by inserting the x -coordinate and y -coordinate from two points on a given line.
The next lessons are
- Rate of change
- Systems of equations
- Number patterns
- Geometry
- Angles
- Angles in parallel lines
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!