How to Factor Quadratic Equations

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Factors and multiples Algebraic expressions Simplifying expressions Equivalent expressions

Multiplying negative numbers

Math resources Algebra Factoring

How to factor quadratic equations

Here you will learn how to factor quadratic equations in order to solve them. You will learn what a quadratic expression is, how to factor a quadratic equation in the form of $x^{2}+bx+c=0$ into two sets of parentheses, and how to factor a quadratic equation in the form of $ax^{2}+bx+c=0$ into two sets of parentheses.

Students first learn how to factor expressions by factoring out the greatest common factor in the $7$ th grade and expand that knowledge as they move into high school math classes.

What is factoring a quadratic equation?

Factoring a quadratic equation is a method to determine the roots of that quadratic. In order to factor a quadratic equation, it is essential to understand what a quadratic equation is. A quadratic equation is a combination of terms where the highest power or exponent is $2.$ The general form or standard form of a quadratic equation is:

$ax^{2}+bx+c=0$

$a$ is the coefficient (number in front) of the $x^2$ term

$b$ is the coefficient (number in front) of the $x$ term

$c$ is the the constant term (a number on its own)

Whether you are factoring (factorizing) a quadratic expression or factoring a quadratic equation to solve it, the strategies of factoring are the same. There are different methods to factor algebraic expressions, the focus here is going to be on factoring the quadratic into two sets of brackets (parentheses).

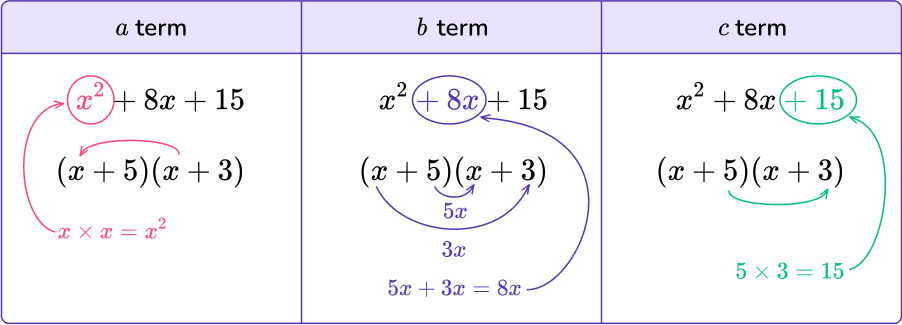
For example, let’s factor the quadratic expression, $x^{2}+8x+15.$

The $a$ term $($ the term including the coefficient of $x^2)$ can be rewritten as $1$ times $x$ times $x$ because $x^{2}=x\cdot{x}$ and $a=1.$

Each of the two pairs of parentheses can therefore start with $x$ as when you expand these, you get $x\cdot{x}=x^{2}.$

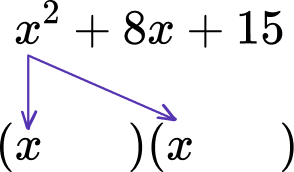
List the factor pairs of the $c$ term (the constant term):

1, 15

3, 5

The $b$ term $($ the term including the coefficient of $x)$ is $8,$ so look for the factor pairs that multiply to $15$ and sum to $8.$

\begin{aligned} 1\times15&=15\\\\ 1+15&=16 \; {\color{red} ✘} \end{aligned}

\begin{aligned} 3\times5&=15\\\\ 3+5&=8\ {\color{lightgreen} ✔} \end{aligned}

The factors of $3$ and $5$ multiply to $15$ and add to $8.$ Place each of these into the parentheses to get $(x+3)(x+5).$

$x^{2}+8x+15$ written in its factored form is $(x+3)(x+5).$

Note: The two pairs of parentheses can be written in any order. Here, $(x+3)(x+5)$ is the same as $(x+5)(x+3)$ as both would expand to be $x^{2}+8x+15.$

Reversing the process, you can see how the $c$ term is the product of the factors, and the $b$ term is the sum of the factors (of the $c$ term).

The quadratic equation, $x^{2}+8x+13=-2$ can be solved using the same strategy, however before factoring a quadratic equation, it is essential that the equation is equal to $0;$ the zero product property.

You can easily make the equation equal to $0$ by adding the $2$ to both sides.

\begin{aligned} x^{2}+8x+13&=-2\\\\ x^{2}+8x+13+2&=-2+2\\\\ x^{2}+8x+15&=0 \end{aligned}

Once the equation is equal to $0,$ you can factor the quadratic into two sets of parentheses using the same strategy as factoring quadratic expressions.

$x^{2}+8x+15=0$ is factored to become $(x+5)(x+3)=0.$

Once the quadratic equation is factored, you are able to solve it $($ find solutions for $x).$

If $p\times{q}=0$ then either $p=0$ or $q=0.$ So as the product of the two pairs of parentheses is equal to $0,$ each pair of parentheses could equal $0.$

Here, $x+5=0$ or $x+3=0.$

Solve each of the equations for $x.$

When $x+5=0,$

\begin{aligned} x+5-5&=0-5\\\\ x&=-5. \end{aligned}

When $x+3=0,$

\begin{aligned} x+3-3&=0-3\\\\ x&=-3. \end{aligned}

The two solutions to the quadratic equation $x^{2}+8x+13=-2$ are:

$x=-5$ and $x=-3.$

You can check your solutions by substituting them one at a time into the original equation.

Check $x=-5.$

\begin{aligned} (-5)^{2}+8(-5)+13&=\\\\ 25-40+13&=\\\\ -15+13&=-2 \; \color{green} ✔ \end{aligned}

Check $x=-3.$

\begin{aligned} (-3)^{2}+8(-3)+13&=\\\\ 9-24+13&=\\\\ -15+13&=-2 \; \color{green} ✔ \end{aligned}

Let’s look at another example, where the coefficient of the $a$ term is something other than $1.$

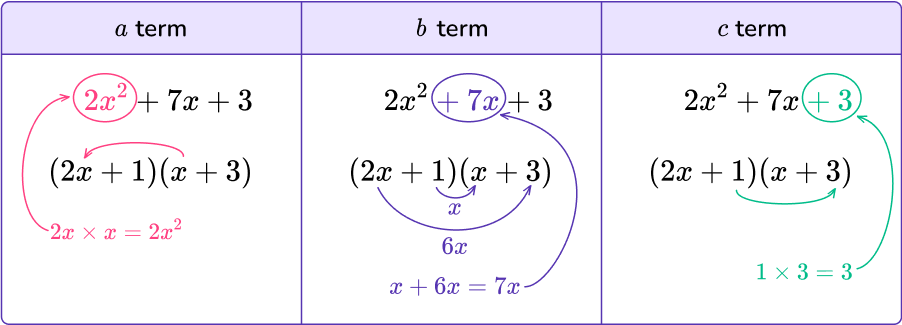
Factor the quadratic expression $2x^{2}+7x+3.$

As the $a$ term can be written as $2x$ times $x,$ the two pairs of parentheses start with $2x$ and $x$ as when you expand these, you get $2x\times{x}=2x^{2}.$

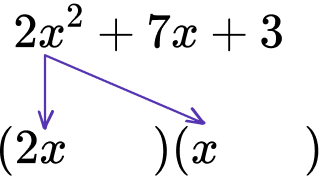
Since the $a$ term has a coefficient greater than $1,$ work out the factors of $a\cdot{c}$ that sum to equal the value of $b$ in the $b$ term.

As $a\times{c}=2\times3=6,$ list the factor pairs of $6$ to find which have a sum of $7.$

Factors of $6 \text{:}$

2, 3

1, 6

\begin{aligned} 2+3&=5 \; \color{red} ✘ \\\\ 1+6&=7 \; \color{green} ✔ \end{aligned}

The two factors that multiply to get $6$ and sum to get $7$ are $1$ and $6.$

As the first pair of parentheses contains $2x,$ the factor in the second bracket is multiplied by $2,$ therefore you must halve the factor in the second pair of parentheses.

As $6$ is an even number, you can easily divide this by $2$ to get $3$ so you need to place the factor of $1$ in the first pair of parentheses and $3$ into the second pair of parentheses to get $(2x+1)(x+3).$

$2x^{2}+7x+3$ in factored form is $(2x+1)(x+3).$

Now, let’s check to be sure that when the binomials are multiplied, it matches the original quadratic.

Remember to use the distributive property in order to multiply the binomials together.

Step-by-step guide: Distributive property

Here, each product obtains the correct term from the original quadratic expression, so the factored form is correct.

The quadratic equation, $2x^{2}+7x+3=0$ can be solved by using the same factoring strategy.

As the factored form of $2x^{2}+7x+3$ is $(2x+1)(x+3),$ you can solve the quadratic $(2x+1)(x+3)=0.$

When $2x+1=0,$

\begin{aligned} 2x+1-1&=0-1\\\\ 2x&=-1\\\\ \cfrac{2x}{2}&=\cfrac{-1}{2}\\\\ x&=-\cfrac{1}{2}\\\\ \end{aligned}

When $x+3=0,$

\begin{aligned} x+3-3&=0-3\\\\ x&=-3 \end{aligned}

The two solutions to the quadratic are $x=-\cfrac{1}{2}$ and $x=-3.$

You can check each solution to make sure it is correct by substituting them, one at a time, back into the original equation.

Check $x=-\cfrac{1}{2}.$

\begin{aligned} 2x^{2}+7x&=\\\\ 2\left(-\cfrac{1}{2}\right)^{2}+7\left(-\cfrac{1}{2}\right)&=\\\\ 2\cdot\cfrac{1}{4}-\cfrac{7}{2}&=\\\\ \cfrac{2}{4}-\cfrac{7}{2}&=\\\\ \cfrac{1}{2}-\cfrac{7}{2}&=\\\\ -\cfrac{6}{2}&=-3 \; \color{green} ✔ \\\\ \end{aligned}

Check $x=-3.$

\begin{aligned} 2x^{2}+7x&=\\\\ 2(-3)^{2}+7(-3)&=\\\\ 2\cdot9-21&=\\\\ 18-21&=-3 \; \color{green} ✔ \\\\ \end{aligned}

What is factoring a quadratic equation?

Common Core State Standards

How does this relate to high school math?

High School Algebra – Seeing Structure in Expressions (HSA-SSE.B.3a)
Factor a quadratic expression to reveal the zeros of the function it defines.

High School Algebra – Reasoning with Equations and Inequalities (HSA-REI.B.4)
Solve quadratic equations in one variable.

[FREE] Algebra Worksheet (Grade 6 to 8)

Use this quiz to check your grade 6 – grade 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th to 8th grade algebra topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Algebra Worksheet (Grade 6 to 8)

DOWNLOAD FREE

In order to factor a quadratic equation when the coefficient of the $a$ term is $1\text{:}$

Find two factors of the constant, $\textbf{c}$ term, that sum to equal the coefficient of the $\textbf{b}$ term.
Write the quadratic in factored form with two sets of parentheses.
Check your work and write the quadratic equation in factored form.

Factor quadratic equations examples

Example 1: quadratic expression with the coefficient of a = 1

Factor the quadratic expression.

x^{2}-2x-24

Find two factors of the constant, $\textbf{c}$ term, that sum to equal the coefficient of the $\textbf{b}$ term.

The constant, $c$ term, is $-24$ so one factor must be negative. The factors of $-24$ are:

\begin{array}{rl} 1,&-24\\\\ -1,&24\\\\ 2,&-12\\\\ -2,&12\\\\ 3,&-8\\\\ -3,&8\\\\ 4,&-6\\\\ -4,&6\\\\ \end{array}

The coefficient of the $b$ term is $-2.$

The two factors that multiply to $-24$ and add to $-2$ are $4$ and $-6.$

\begin{aligned} 4\cdot(-6)&=-24\\\\ 4+-6&=-2\\\\ \end{aligned}

2Write the quadratic in factored form with two sets of parentheses.

The $a$ term breaks up to be $x\cdot{x}$ and $x\cdot{x}=x^{2}$

x^{2}-2x-24=(x-6)(x+4)

3Check your work and write the quadratic equation in factored form.

You can check your work through distributive property.

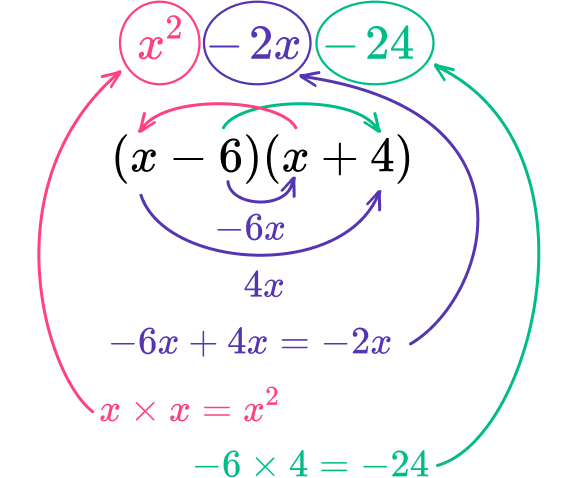
Example 2: factor quadratic equation

Factor the quadratic equation.

x^{2}+5x+6

Find two factors of the constant, $\textbf{c}$ term, that sum to equal the coefficient of the $\textbf{b}$ term.

The $c$ term is $6$ and the coefficient of the $b$ term is $5.$ As the coefficient of the $b$ term is positive, both the factors to find are positive.

Find two factors that multiply to be $6$ and add to $5.$

Factors of $6\text{:}$

\begin{array}{cc} 1,&6\\\\ 2,&3\\\\ \end{array}

The factors of $6$ that add to get $5$ are $2$ and $3.$

\begin{aligned} 2\cdot3&=6\\\\ 2+3&=5\\\\ \end{aligned}

Write the quadratic in factored form with two sets of parentheses.

(x+3)(x+2)

Note: this can also be written as $(x+2)(x+3)$ because of the commutative property of multiplication.

Check your work and write the quadratic equation in factored form.

You can check your work by using the distributive property.

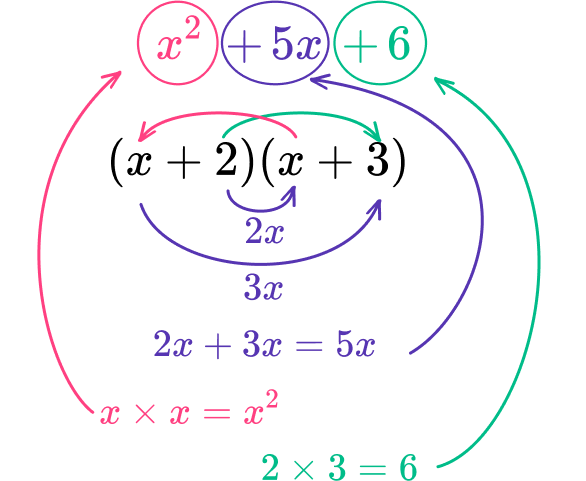
The quadratic was factored correctly.

$x^{2}+5x+6=(x+3)(x+2)$

Example 3: quadratic equation with different signs

Factor the quadratic equation, $x^{2}-8x+16=0.$

Find two factors of the constant, $\textbf{c}$ term, that sum to equal the coefficient of the $\textbf{b}$ term.

The coefficient of the $b$ term is $-8$ and the $c$ term is $16.$ As the $c$ term is positive and the coefficient of the $b$ term is negative, both factors must be negative.

Factors of $16\text{:}$

\begin{array}{cc} -1,& -16\\\\ -2,& -8\\\\ -4,& -4\\\\ \end{array}

The factors of $16$ that sum to $-8$ are $-4$ and $-4.$

\begin{aligned} 4\cdot4&=16\\\\ -4-4&=-8\\\\ \end{aligned}

Write the quadratic in factored form with two sets of parentheses.

$(x-4)(x-4)$ which can also be written as $(x-4)^{2}.$

Check your work and write the quadratic equation in factored form.

You can check your work by using the distributive property.

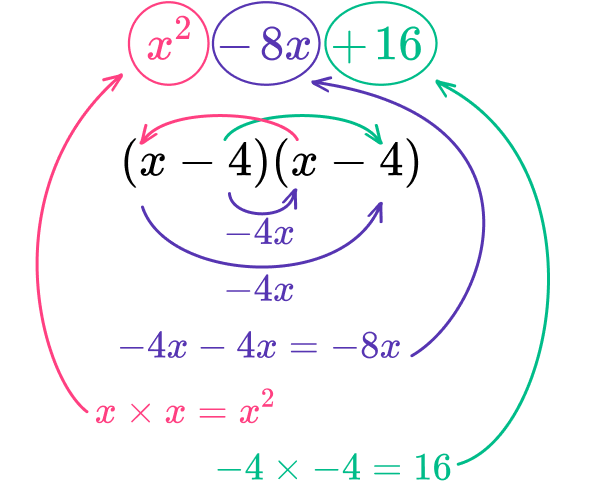
The quadratic was factored correctly.

$x^{2}-8x+16=(x-4)(x-4)$

How to factor quadratic equations

In order to factor a quadratic equation when the $a$ term is not $1:$

Find the factors of $\textbf{ac}$ that sum to equal the coefficient of the $\textbf{b}$ term.
Place the factors in the parentheses and check to make sure the product of the inside terms and outside terms sum to the $\textbf{b}$ term.
Write the quadratic equation in factored form.

Example 4: ax² + bx + c where a is not 1

Factor the quadratic, $5x^{2}+6x+1.$

Find the factors of $\textbf{ac}$ that sum to equal the coefficient of the $\textbf{b}$ term.

The value of $ac$ is $5\times{1}=5.$

The factors of $5$ are $1$ and $5.$

The coefficient of the $b$ term is $6.$ The factors of $5$ that sum to $6$ are $1$ and $5.$

Place the factors in the parentheses and check to make sure the product of the inside terms and outside terms sum to the $\textbf{b}$ term.

The $a$ term is $5x^{2}$ which you can factor into $5x$ and $x.$

So far, the factored quadratic looks like: $(5x\ \ \ \ \ )(x\ \ \ \ \ \ )$

As one of the parentheses contains $5x,$ the factor in the other bracket is multiplied by $5,$ therefore you must divide the factor by $5$ in the other bracket.

As $5$ is a multiple of $5,$ you can easily divide this by $5$ to get $1$ so you need to place the factor of $1$ in the first pair of parentheses and $1$ into the second pair of parentheses to get $(5x+1)(x+1).$

Now check the expansion.

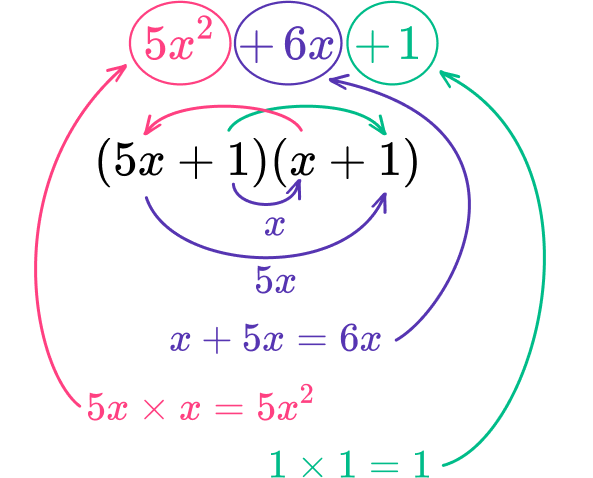
Each term is correct.

Write the quadratic equation in factored form.

5x^{2}+6x+1=(5x+1)(x+1)

Example 5: ax² + bx + c where a is not 1 and the signs are different

Factor the expression, $2x^{2}+3x-2$ .

Find the factors of $\textbf{ac}$ that sum to equal the coefficient of the $\textbf{b}$ term.

The value of $ac$ is $2\times{-2}=-4.$

As $-4$ is a negative number, one factor must be negative. The factors of $-4$ are

\begin{array}{cc} -1,&-4\\\\ 1,&-4\\\\ 2,&-2\\\ \end{array}

The coefficient of the $b$ term is $3.$ The factors of $-4$ that sum to $3$ are $-1$ and $4.$

Place the factors in the parentheses and check to make sure the product of the inside terms and outside terms sum to the $\textbf{b}$ term.

The $a$ term is $2x^{2}$ which you can factor into $2x$ and $x.$

So far, the factored quadratic looks like: $(2x\ \ \ \ \ )(x\ \ \ \ \ \ )$

As one of the parentheses contains $2x,$ the factor in the other bracket is multiplied by $2,$ therefore you must divide the factor by $2$ in the other bracket.

As $4$ is a multiple of $2,$ you can easily divide this by $2$ to get $2$ so you need to place the factor of $-1$ in the first pair of parentheses and $2$ into the second pair of parentheses to get $(2x-1)(x+2).$

Now check the expansion.

Write the quadratic equation in factored form.

2x^{2}+3x-2=(2x-1)(x+2)

Example 6: ax² + bx + c = 0 where a is not 1

Factor the quadratic equation, $3x^{2}-4x+1=0.$

Find the factors of $\textbf{ac}$ that sum to equal the coefficient of the $\textbf{b}$ term.

The value of $ac$ is $3\times{1}=3$

As $3$ is a positive number but the $b$ term is a negative number, both factors must be negative. The factors of $3$ are,

$-1, -3$

There is only one pair of factors, which must add to get the coefficient of the $b$ term.

$(-1)+(-3)=-4$

The factors of $3$ that add to $-4$ are $-1$ and $-3.$

Place the factors in the parentheses and check to make sure the product of the inside terms and outside terms sum to the $\textbf{b}$ term.

The $a$ term is $3x^{2}$ which you can factor into $3x$ and $x.$

So far, the factored quadratic looks like: $(3x\ \ \ \ \ )(x\ \ \ \ \ \ )=0$

As one of the parentheses contains $3x,$ the factor in the other bracket is multiplied by $3,$ therefore you must divide the factor by $3$ in the other bracket.

As $-3$ is a negative multiple of $3,$ you can easily divide this by $3$ to get $-1$ so you need to place the factor of $-1$ in the first pair of parentheses and $-1$ into the second pair of parentheses to get $(3x-1)(x-1)=0.$

Now check the expansion.

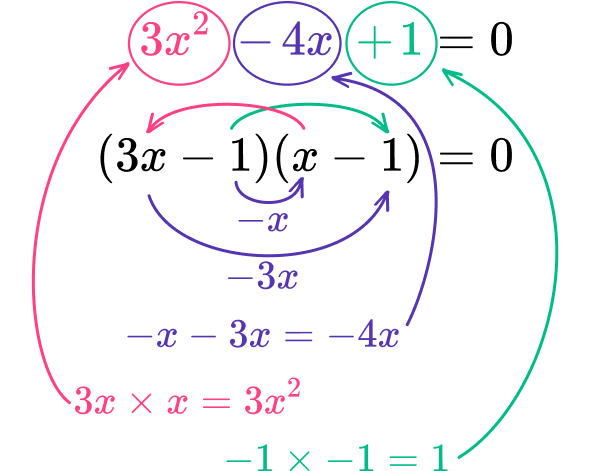
Write the quadratic equation in factored form.

$3x^{2}-4x+1=0$ in factored form is $(3x-1)(x-1)=0$

Teaching tips for how to factor quadratic equations

Use manipulatives such as algebra tiles so that students can visualize how to factor quadratics.

Enhance understanding of the distributive function when expanding binomials and polynomials.

Use whiteboards or rough paper to explore different factors.

Visualize the quadratic equation by using a graph of the function.

Easy mistakes to make

Mixing up the signs of the factors in the brackets
For example, factoring the quadratic $x^{2}-2x-24$ into $(x+6)(x-4).$

$(x+6)(x-4)$ is not the correct factored form of the quadratic. When multiplying out the two sets of parentheses, you can see that it is not factored correctly.

$\begin{aligned} &(x+6)(x-4)\\ &=x^{2}-4x+6x+24 \end{aligned}$
$=x^{2}+2x+24$ ≠ ${x}^{2}-2x+24$

By switching the signs around, the expression is in the correct factored form.
$(x-6)(x+4)=x^{2}-2x-24$

Thinking that the order of the parentheses matter
For example, thinking that $(x-5)(x+3)$ ≠ $(x+3)(x-5).$
When using the distributive property to multiply them both out, you can see that they are the same and the order of the parentheses does not matter.

$(x-5)(x+3)$
$=(x-5)(x+3)=x^{2}+3x-5x-15$
$=x^{2}-2x-15$

$(x+3)(x-5)$
$=x^{2}-5x+3x-15$
$=x^{2}-2x-15$

Incorrect terms used
A quadratic may be written in an unusual form e.g. $5x+x^{2}+6$ or $x^{2}=8x-16.$ In $5x+x^{2}+6,$ the coefficient of the $a$ term is $1,$ not $5$ as the $a$ term contains $x^{2}.$

In $x^{2}=8x-16,$ the coefficient of the $b$ term is $-8,$ not $8$ as the quadratic is currently not equal to $0.$

The coefficients and constant term values can only be used when the quadratic is in the form $ax^{2}+bx+c$ or $ax^{2}+bx+c=0.$ The quadratic must be rearranged first.

Factoring
Factoring out the GCF
Factoring the difference of two squares
Factor by grouping

Practice questions on how to factor quadratic equations

(x+5)(x+6)=0

(x+3)(x+2)=0

(x+1)(x+6)=0

(x+3)(x+3)=0

For the quadratic equation, $x^{2}+5x+6=0,$ you need to find two factors that multiply to $6$ and sum to $5.$ The factors to use are $2$ and $3$ because:

$2\times3=6$ and $2+3=5$

So, $x^{2}+5x+6=0$ in its factored form is $(x+3)(x+2)=0.$

Note, $(x+2)(x+3)=0$ is also correct.

(x+3)(x+7)

(x+1)(x+21)

(x+10)(x+21)

(x+1)(x+10)

For the quadratic expression, $x^{2}+10x+21,$ you need to find two factors that multiply to $21$ and sum to $10.$ The factors to use are $3$ and $7$ because:

$3\times7=21$ and $3+7=10$

So, $x^{2}+10x+21=(x+3)(x+7)$ which can also be written as $(x+7)(x+3).$

(x+4)(x-3)

(x-1)(x+12)

(x-1)(x-12)

(x-4)(x+3)

For the quadratic expression, $-x+x^{2}-12,$ rearrange it first so that it is in the usual format of $x^{2}-x-12.$ You then need to find two factors that multiply to $-12$ and sum to $-1.$ The factors to use are $-4$ and $3$ because:

$3\times{-4}=-12$ and $3+(-4)=-1$

So, $-x+x^{2}-12=(x+3)(x-4)$ which can also be written as $(x-4)(x+3).$

x(x+3)=18

(x+6)(x+3)=0

(x+3)(x-6)=0

(x-6)(x-3)=0

For the quadratic eqquation, $x^{2}+3x=18,$ rearrange it first so that it is equal to $0.$ You now have $x^{2}+3x-18=0.$ You then need to find two factors that multiply to $-18$ and sum to $3.$ The factors to use are $-6$ and $3$ because:

$3\times{-6}=-18$ and $3+(-6)=-3$

So, $x^{2}+3x=18$ in its fully factored form is $(x+3)(x-6)=0.$

(2x-5)(x+1)

(2x+5)(x-1)

(2x+1)(x-5)

(2x-1)(x+5)

For the quadratic, $2x^{2}+3x-5$ the value of $ac$ is $2\times{-5}=-10.$ The factors of $-10$ that have a sum of $3$ are $-2$ and $5.$ The $a$ term can be factored into $2x$ and $x$ so the factored form is currently $(2x\ \ \ \ \ )(x\ \ \ \ \ \ ).$

As one of the parentheses contains $2x,$ the factor in the other bracket is multiplied by $2,$ therefore divide the factor by $2$ in the other bracket.

As $-2$ is a negative multiple of $2,$ you can easily divide this by $2$ to get $-1$ so $5$ is in the first pair of parentheses and $-1$ is in the second pair to get $(2x+5)(x-1).$

(3x+1)(x+2)

(3x-1)(x+2)

(3x-1)(x-2)

(3x+1)(x-2)

For the quadratic, $3x^{2}-7x+2=0$ the value of $ac$ is $3\times{2}=6.$ The factors of $6$ that have a sum of $-7$ are $-1$ and $-6.$ The $a$ term can be factored into $3x$ and $x$ so the factored form is currently $(3x\ \ \ \ \ )(x\ \ \ \ \ \ ).$

As one of the parentheses contains $3x,$ the factor in the other bracket is multiplied by $3,$ therefore divide the factor by $3$ in the other bracket.

As $-6$ is a negative multiple of $3,$ you can easily divide this by $3$ to get $-2$ so $-1$ is in the first pair of parentheses and $-2$ is in the second pair to get $(3x-1)(x-2).$

How to factor quadratic equations FAQs

How do you solve quadratic equations that do not factor?

You can use the quadratic formula to solve all quadratic equations. However, the quadratic formula is typically used when a quadratic equation cannot be factored, meaning that the quadratic equation is prime.

What is a perfect square trinomial?

A perfect square trinomial is a quadratic expression that factors into two
identical set of parentheses. For example, the quadratic, $x^{2}+6x+9$ is considered to be a perfect square trinomial because it factors to be, $(x+3)(x+3)$ which can be written as $(x+3)^2.$

Can you factor polynomials?

Yes, you can factor polynomials. Quadratics can be factored and they are a type of polynomial – quadratic polynomials. However, other polynomials with higher degrees can be factored too, which you will learn in Algebra II and Precalculus.

Can you factor quadratics that have a fraction or a negative number as a leading coefficient?

Yes, quadratics can be factored with fractional or negative number coefficients.

Can any real number be the coefficients of a quadratic?

Yes, quadratic equations or polynomial equations can have any real number as a coefficient.

Can you factor linear equations?

Yes, you can factor linear equations by using the method of factoring out the GCF.

The next lessons are

Radicals
Radical functions
Vectors

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.