High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Math equations Place value Decimal place value Comparing decimals Comparing fractionsGreater than sign
Here you will learn about the greater than sign, including the symbol used to represent it and how to compare numbers and fractions using the greater than sign.
Students will first learn about the greater than sign as part of the number and operations in base 10 and number and operations – fractions in elementary school.
What is the greater than sign?
The greater than sign is a mathematical symbol used to compare numbers and expressions.
It is one of the symbols used for inequalities along with the less than symbol, <.
When stacking identical blocks, the height of 3 blocks is greater than the height of 1 block. The lines joining the stacks give the shape and direction of the inequality symbols.
The greater than sign is,
The greater than sign is also known as the more than sign. The wide end of the symbol always faces the bigger number or expression – the symbol looks open towards the bigger number and ‘points’ at the smaller value like an arrow.
For example,
This is read as ‘10 is greater than 6’.
The greater than sign is used to compare;
is greater than 10’. | ||
|---|---|---|
greater than 1.8’. | ||
greater than one third’. |
What is the greater than sign?
![[FREE] Greater Than Sign Worksheet (Grade 1 to 5)](data:image/svg+xml;nitro-empty-id=NjYwOjYwMg==-1;base64,PHN2ZyB2aWV3Qm94PSIwIDAgNDUwIDE5NSIgd2lkdGg9IjQ1MCIgaGVpZ2h0PSIxOTUiIHhtbG5zPSJodHRwOi8vd3d3LnczLm9yZy8yMDAwL3N2ZyI+PC9zdmc+)
[FREE] Greater Than Sign Worksheet (Grade 1 to 5)
![[FREE] Greater Than Sign Worksheet (Grade 1 to 5)](data:image/svg+xml;nitro-empty-id=NjY0OjU4Ng==-1;base64,PHN2ZyB2aWV3Qm94PSIwIDAgNDUwIDE5NSIgd2lkdGg9IjQ1MCIgaGVpZ2h0PSIxOTUiIHhtbG5zPSJodHRwOi8vd3d3LnczLm9yZy8yMDAwL3N2ZyI+PC9zdmc+)
Use this worksheet to check your 1st to 5th grade students’ understanding of the greater than sign. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Greater Than Sign Worksheet (Grade 1 to 5)](data:image/svg+xml;nitro-empty-id=NjgxOjYwMg==-1;base64,PHN2ZyB2aWV3Qm94PSIwIDAgNDUwIDE5NSIgd2lkdGg9IjQ1MCIgaGVpZ2h0PSIxOTUiIHhtbG5zPSJodHRwOi8vd3d3LnczLm9yZy8yMDAwL3N2ZyI+PC9zdmc+)
[FREE] Greater Than Sign Worksheet (Grade 1 to 5)
![[FREE] Greater Than Sign Worksheet (Grade 1 to 5)](data:image/svg+xml;nitro-empty-id=Njg1OjU4Ng==-1;base64,PHN2ZyB2aWV3Qm94PSIwIDAgNDUwIDE5NSIgd2lkdGg9IjQ1MCIgaGVpZ2h0PSIxOTUiIHhtbG5zPSJodHRwOi8vd3d3LnczLm9yZy8yMDAwL3N2ZyI+PC9zdmc+)
Use this worksheet to check your 1st to 5th grade students’ understanding of the greater than sign. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this relate to 1st grade, 2nd grade, 3rd grade, 4th grade, and 5th grade math?
- Grade 1: Number and Operations in Base Ten (1.NBT.B.3)
Compare two two-digit numbers based on meanings of the tens and ones digits, recording the results of comparisons with the symbols >, \, =, and <.
- Grade 2: Number and Operations in Base Ten (2.NBT.A.4)
Compare two three-digit numbers based on meanings of the hundreds, tens, and ones digits, using >, \, =, and < symbols to record the results of comparisons.
- Grade 3: Number and Operations – Fractions (3.NF.A.3d)
Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, \, =, or <, and justify the conclusions, for example, by using a visual fraction model.
- Grade 4: Number and Operations in Base Ten (4.NBT.A.2)
Read and write multi-digit whole numbers using base-ten numerals, number names, and expanded form. Compare two multi-digit numbers based on meanings of the digits in each place, using >, \, =, and < symbols to record the results of comparisons.
- Grade 4: Number and Operations – Fractions (4.NF.A.2)
Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as \frac{1}{2}. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols > , \, =, or <, and justify the conclusions, for example, by using a visual fraction model.
- Grade 5: Number and Operations in Base Ten (5.NBT.3b)
Compare two decimals to thousandths based on meanings of the digits in each place, using >, \, =, and < symbols to record the results of comparisons.
How to compare values using the greater than sign
In order to compare values using the greater than sign:
- Write the given numbers into a place value chart.
- Starting with the greatest place value, compare the digits of the number, until you find digits that are different.
- Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.
Greater than sign examples
Example 1: comparing two-digit numbers
Write the correct sign, > or <, in the box.
- Write the given numbers into a place value chart.
2Starting with the greatest place value, compare the digits of the number, until you find digits that are different.
Looking at the place value chart, start comparing the greatest place value, the tens place.
32 has 3 tens and 17 has 1 ten. You know that 3 tens is greater than 1 ten, therefore, 32 is the greater number.
3Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.
32 is greater than 17.
Place the wide end of the symbol towards the 32, with the point facing the smaller number, 17.
Example 2: comparing three-digit numbers
Write the correct sign, > or <, in the box.
Write the given numbers into a place value chart.
Starting with the greatest place value, compare the digits of the number, until you find digits that are different.
Start comparing the numbers in the hundreds place.
The digits in the hundreds place are the same, so you will move to the tens place to compare.
261 has 6 tens and 285 has 8 tens. You know that 8 tens is greater than 6 tens, therefore, 285 is the larger number.
Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.
285 is greater than 261.
Place the wide end of the symbol towards the 285, with the point facing the smaller number, 261.
Example 3: comparing multi-digit numbers
Write the correct sign, > or <, in the box.
Write the given numbers into a place value chart.
Starting with the greatest place value, compare the digits of the number, until you find digits that are different.
You will start comparing the numbers in the thousands place.
The digits in the thousands place are the same, so move to the hundreds place to compare.
The digits in the hundreds place are the same, so move to the tens place to compare.
The digits in the tens place are the same, so move to the ones place to compare.
4,813 has 3 ones and 4,812 has 2 ones. 3 ones is greater than 2 ones, therefore, 4,813 is the greater number.
Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.
4,813 is greater than 4,812.
Place the wide end of the symbol towards 4,813, with the point facing the smaller number, 4,812.
Example 4: comparing decimals
Write the correct sign, > or <, in the box.
Write the given numbers into a place value chart.
Starting with the greatest place value, compare the digits of the number, until you find digits that are different.
Start comparing the numbers in the ones place.
The digits in the ones place are the same, so move to the tenths place to compare.
The digits in the tenths place are the same, so move to the hundredths place to compare.
7.82 has 2 hundredths and 7.802 has 0 hundredths. 2 hundredths is greater than 0 hundredths, therefore, 7.82 is the greater number.
Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.
7.82 is greater than 7.802.
Place the wide end of the symbol towards 7.82, with the point facing the smaller number, 7.802.
How to compare fractions using the greater than sign
In order to compare fractions using the greater than sign:
- See if the fractions have equal numerators or denominators.
- Use equivalent fractions to find a common denominator if needed.
- Compare the fractions and write the answer using the original fractions and correct comparison symbol.
Example 5: comparing fractions with same numerator
Which is larger, \, \cfrac{4}{5} \, or \, \cfrac{4}{8} \, ? Write your answer using the greater than comparison symbol.
See if the fractions have equal numerators or denominators.
The fractions \, \cfrac{4}{5} \, and \, \cfrac{4}{8} \, have the same numerators (top numbers).
Use equivalent fractions to find a common denominator if needed.
You will not need to make equivalent fractions, because you can compare with common numerators.
Compare the fractions and write the answer using the original fractions and correct comparison symbol.
Compare the fractions \, \cfrac{4}{5} \, and \, \cfrac{4}{8} \, to determine which is larger.
Because the fractions have the same numerator, use the denominator to determine which is larger. The smaller the denominator, the larger each piece of the whole will be. The larger the denominator, the smaller each part of the whole will be.
Fifths are larger, so 4 fifths will be larger than 4 eighths.
So \, \cfrac{4}{5} \, is larger than \, \cfrac{4}{8} \, .
You write the comparison as \, \cfrac{4}{5} \, > \, \cfrac{4}{8} \, .
Example 6: comparing fractions using common denominator
Which is larger, \, \cfrac{5}{6} \, or \, \cfrac{7}{12} \, ? Write your answer using the greater than comparison symbol.
See if the fractions have equal numerators or denominators.
The fractions do not have the same numerators (top numbers) or denominators (bottom numbers).
Use equivalent fractions to find a common denominator if needed.
To create a common denominator, multiply the numerator and denominator of the fraction \, \cfrac{5}{6} \, by 2 to make a common denominator of 12.
\cfrac{5}{6}=\cfrac{5 \, \times \, 2}{6 \, \times \, 2}=\cfrac{10}{12}
You can also create common denominators by multiplying each fraction by the opposite denominator.
\cfrac{5}{6}=\cfrac{5 \, \times \, 12}{6 \, \times \, 12}=\cfrac{60}{72} \, and \, \cfrac{7}{12}=\cfrac{7 \, \times \, 6}{12 \, \times \, 6}=\cfrac{42}{72}
Compare the fractions and write the answer using the original fractions and correct comparison symbol.
Compare the now equivalent fractions \, \cfrac{10}{12} \, and \, \cfrac{7}{12} \, to determine which is larger.
\cfrac{7}{12} \, has 7 parts shaded in and \, \cfrac{10}{12} \, has 10 parts shaded in.
Since the parts are the same size, \, \cfrac{10}{12} \, is larger.
\cfrac{10}{12} \, is larger than \, \cfrac{7}{12} \, .
You write the comparison as \, \cfrac{5}{6} \, > \, \cfrac{7}{12} \, .
Example 7: comparing fractions using common denominator
Which is larger, \, \cfrac{3}{5} \, or \, \cfrac{2}{7} \, ? Write your answer using the greater than comparison symbol.
See if the fractions have equal numerators or denominators.
The fractions do not have the same denominators (bottom numbers).
Use equivalent fractions to find a common denominator if needed.
To create a common denominator, multiply each fraction by the opposite denominator.
\cfrac{3}{5}=\cfrac{3 \, \times \, 7}{5 \, \times \, 7}=\cfrac{21}{35} \, and \, \cfrac{2}{7}=\cfrac{2 \, \times \, 5}{7 \, \times \, 5}=\cfrac{10}{35}
Compare the fractions and write the answer using the original fractions and correct comparison symbol.
Compare the now equivalent fractions \, \cfrac{21}{35} \, and \, \cfrac{10}{35} \, to determine which is larger.
\cfrac{21}{35} \, has 21 parts shaded in and \, \cfrac{10}{35} \, has 10 parts shaded in.
Since the parts are the same size, \, \cfrac{21}{35} \, is larger.
\cfrac{21}{35} \, is larger than \, \cfrac{10}{35} \, .
You write the comparison as \, \cfrac{3}{5} \, > \, \cfrac{2}{7} \, .
Teaching tips for greater than sign
- When students are first learning to compare numbers, it’s important to allow them to investigate with a hands-on approach. For students in higher grade levels who are continuing to struggle, manipulatives are a great way to reinforce meaning. There will be time for worksheets as practice after students have a better understanding of what it means to compare numbers.
- It is important for students to understand what each symbol means when comparing numbers. These symbols can be displayed in the classroom on an anchor chart or in interactive notebooks while students get familiar with the meanings.
- Although drawing an alligator’s mouth may be amusing for younger primary school kids, they often focus solely on the higher number rather than the complete comparison. Students should be reminded to utilize the math symbols as intended and to emphasize their meanings each time they are used.
Easy mistakes to make
- Confusing the greater than and less than symbols
The biggest mistake is writing the symbols the wrong way round. Remember, the sign should point at the smallest number like an arrow.
For example, 14 \, > \, 7, \, ‘14 is greater than 7’, or 7 \, < \, 14, \, ‘7 is less than 14’.
- Trying to compare fractions without common numerator or denominator
When comparing fractions, the fractions should have either a common numerator or denominator. You may have to convert them into equivalent fractions with common denominators, so you can compare the numerators.
Related inequalities lessons
This greater than sign topic guide is part of our series on inequalities. You may find it helpful to start with the main inequalities topic guide for a summary of what to expect or use the step-by-step guides below for further detail on individual topics. Other topic guides in this series include:
Practice greater than sign questions
1. Which is larger, 57 or 75? Write your answer using the greater than comparison symbol.
Write the numbers you are comparing into a place value chart.
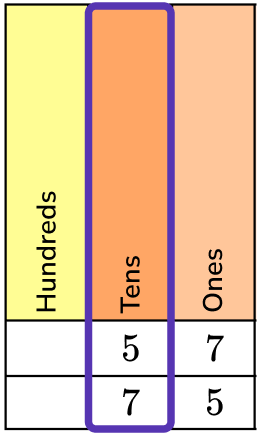
Start with the greatest place value chart, the tens, and compare the digits.
57 has 5 tens and 75 has 7 tens.
7 tens is greater than 5 tens.
75 is greater than 57.
75 > 57.
2. Which is larger, 423 or 432? Write your answer using the greater than comparison symbol.
Write the numbers you are comparing into a place value chart.
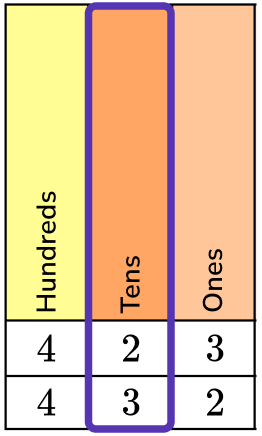
Start with the greatest place value chart and compare the digits.
The digits in the hundreds place are the same, so you would move to the tens place to compare.
423 has 2 tens and 432 has 3 tens.
3 tens is greater than 2 tens.
432 is greater than 423.
432 > 423.
3. Which is larger, 34,568 or 34,768? Write your answer using the greater than comparison symbol.
Write the numbers you are comparing into a place value chart.
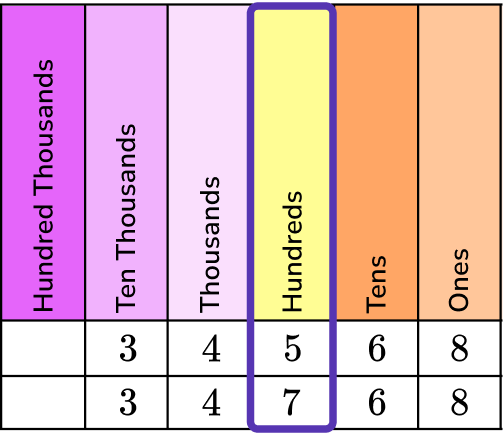
Start with the greatest place value chart and compare the digits.
The digits in the ten thousands place and thousands place are the same, so you would move to the hundreds place to compare.
34,568 has 5 hundreds and 34,768 has 7 hundreds.
7 hundreds is greater than 5 hundreds.
34,768 is greater than 34,568.
34,768 > 34,568.
4. Which is larger, 6.09 or 6.90? Write your answer using the greater than comparison symbol.
Write the numbers you are comparing into a place value chart.
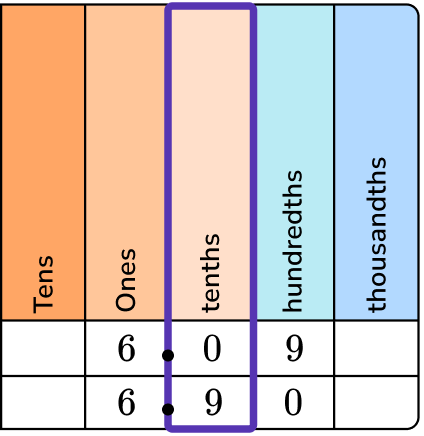
Start with the greatest place value chart and compare the digits.
The digits in the ones place are the same, so you would move to the tenths place to compare.
6.09 has 0 tenths and 6.90 has 9 tenths.
9 tenths is greater than 0 tenths.
6.90 is greater than 6.09.
6.90 > 6.09.
5. Which is larger, \, \cfrac{4}{7} \, or \, \cfrac{4}{9} \, ? Write your answer using the greater than comparison symbol.
The fractions have equal numerators, so you do not need to make equivalent fractions.
Sevenths are larger, so 4 sevenths will be greater than 4 ninths.
Therefore, \, \cfrac{4}{7} \, is greater than \, \cfrac{4}{9} \, .
\cfrac{4}{7} \, > \, \cfrac{4}{9} \, .
6. Which is larger, \, \cfrac{3}{4} \, or \, \cfrac{7}{8} \, ? Write your answer using the greater than comparison symbol.
The fractions do not have the same numerators (top numbers) or denominators (bottom numbers).
To create a common denominator, double the fraction \cfrac{3}{4} to make the common denominator of 8.
\cfrac{3}{4}=\cfrac{3 \, \times \, 2}{4 \, \times \, 2}=\cfrac{6}{8}
Compare the fractions with common denominators \, \cfrac{6}{8} \, and \, \cfrac{7}{8} \, to determine which is larger.
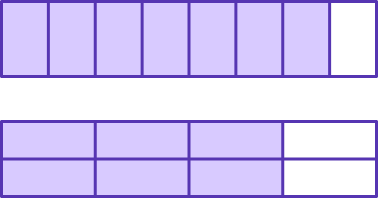
\cfrac{6}{8} \, has 8 parts shaded in and \, \cfrac{7}{8} \, has 7 parts shaded in.
Since the parts are the same size, \, \cfrac{7}{8} \, is larger.
\cfrac{7}{8} \, is larger than \, \cfrac{3}{4} \, .
\cfrac{7}{8} \, > \, \cfrac{3}{4} \, .
Greater than sign FAQs
When using the greater than sign, the first number will be the largest number followed by the second number being the smaller of the two numbers. The two numbers will be separated by the greater than sign, >.
When comparing numbers, you will also use the less than sign, <, the equal sign, =, the less than or equal to sign, ≤, and the greater than or equal to sign, ≥ .
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!