Expanding expressions

Here you will learn how to expand expressions before simplifying the resulting algebraic expressions.

Students will first learn about expanding expressions as part of expressions and equations in 6th grade.

What is expanding expressions?

Expanding expressions (or multiplying out) is the process by which you use the distributive property to remove parentheses from an algebraic expression.

To do this, you need to multiply out the parentheses by multiplying everything outside of the parentheses by everything inside the parentheses. Then, if needed, you simplify the resulting expression by combining the like terms.

For example,

2(x+5) = 2x+10

For this example,

The expression has two sets of parentheses. You will need to simplify by combining like terms after expanding the expression.

\begin{aligned} & 2(x+5)+3(x-1) \\\\ & =2 x+10+3 x-3 \\\\ & =5 x+7 \end{aligned}

What is expanding expressions?

Common Core State Standards

How does this relate to 6th grade math?

• Grade 6 – Expressions and Equations (6.EE.A.3)
  Apply the properties of operations to generate equivalent expressions. For example, apply the distributive property to the expression 3 \, (2 + x) to produce the equivalent expression 6 + 3x; apply the distributive property to the expression 24x + 18y to produce the equivalent expression 6 \, (4x + 3y); apply properties of operations to y + y + y to produce the equivalent expression 3y .

How to expand expressions

In order to expand expressions:

1. Use the distributive property to “multiply out” the parentheses in the expression.
2. Combine the like terms.

Expanding expressions examples

Example 1: one set of parentheses

Expand:

9 \, (y+6)

1. Use the distributive property to “multiply out” the parentheses in the expression.

\begin{aligned} & 9 \, (y+6) \\\\ & =(9 \times y)+(9 \times 6) \\\\ & =9 y+54 \end{aligned}

2Combine the like terms.

There are no like terms in the expression, so you are finished.

The expanded expression is 9y+54 .

Example 2: one set of parentheses

Expand and simplify:

6 \, (𝑡 + 8)–12

Example 3: one set of parentheses

5 b+7(b-2)-18

Example 4: two sets of parentheses

Expand and simplify:

8(x-2)+6(x+3)

Combine the like terms.

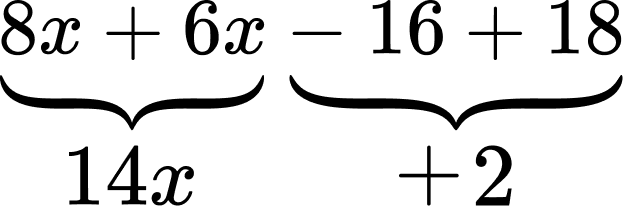
First, use the commutative property to group the like terms together.

Underline the two x terms (8x and +6x) and combine them. Then do the same for the two constants (-16 and +18). Remember to underline the sign in front of the number too!

8 x+6 x=14 x

-16 and +18 = 2

(Note that -16 + 18 can also be written as 18-16 ).

So the expanded and simplified expression is 14x + 2 .

Example 5: constants and variables outside of the parentheses

Expand and simplify:

2 x(x+6)-3(x-2)

Example 6: variables in both terms in the parentheses

Expand and simplify:

3 \, (2 x-6 y)-5 \, (x-2 y)

Use the distributive property to “multiply out” the parentheses in the expression.

Multiply the first set of parentheses. Another method you can use is to write the terms in an area model:

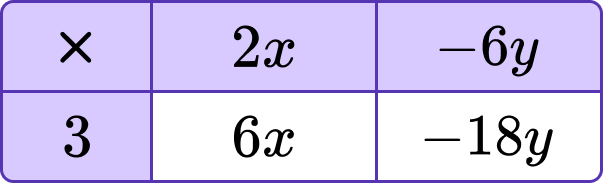
(A positive number times a negative number equals a negative number so 3 \times -6y gives a negative answer. You need to write -18y ).

The first set of parentheses expands to 6x–18y .

Multiply out the second set of parentheses. Remember, you are multiplying both x and -2y by -5 .

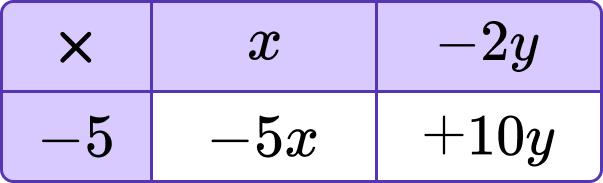
(A negative number times a negative number equals a positive number so -5 \times -2y gives a positive answer. You need to write +10y ).

The second set of parentheses expands to –5x + 10y .

The expression is now,

6 x-18 y-5 x+10 y

Combine the like terms.

Underline the two x terms (6x and -5x) and the two y terms (-18y and +10y).

Remember to underline the sign in front of the number too.

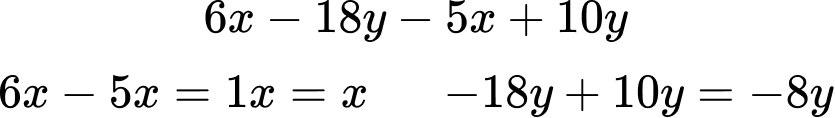
The expanded and simplified expression is x-8y .

Teaching tips for expanding expressions

• Assess students’ prior knowledge before beginning. Review key vocabulary terms including algebraic expression, parentheses, simplify, exponents, distributive property, binomial, polynomial, terms, coefficients. Review adding and subtracting negative numbers as needed.

• Allowing learners to use templates or organizers when practicing this skill or completing worksheets, such as the area model shown above, will help them organize their work as they complete the process step-by-step.

• Be sure students have had plenty of practice expanding expressions with one set of parentheses before moving on to expanding expressions with binomials or polynomials.

• The expanding expression tool kit you will provide students is essential for higher levels of mathematics.

Easy mistakes to make

• Multiplying all terms in the set of parentheses
  You must multiply the term outside the parentheses by every term inside the parentheses.
  For example,
  
  2\left(6 x^2-3 x\right)=12 x^2-3 x
  
  Here, you have not multiplied the value outside of the parentheses by the second term. The correct answer is:
  
  2\left(6 x^2-3 x\right)=12 x^2-6 x

• Squaring a term
  When you square something, you multiply it by itself.
  For example,
  
  \begin{aligned} 3^{2}&=3\times 3\\ x^{2}&=x\times x\\ (5y)^{2}&=5y\times 5y \end{aligned}

• Combining like terms
  When you combine like terms, you must include the sign in front of the number. Be sure to underline the sign along with the number when combining the like terms.
  For example,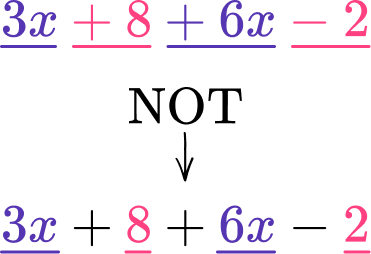
  
  

  

Related algebraic expressions lessons

• Algebraic expression
• Simplifying expressions
• Combining like terms
• Equivalent expressions
• Evaluate the expression

The next lessons are

• Math equations
• Inequalities
• Types of graphs
• Fractions

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.