What is the sum? A Guide For Teachers And Students

How many times do you ask yourself: What is the sum? How many do I have altogether? Finding the sum, or the total, is something we do daily. It is one of the most important concepts in mathematics and is explored as early as kindergarten.

Finding the sum is a foundational skill for other mathematical concepts such as subtraction, multiplication, and division. The concept of a sum is also applied in higher mathematics concepts such as arithmetic sequences with given numbers and natural numbers.

This blog explores the importance of the concept of a sum and how it is used to solve real-world mathematics problems and allow learners to become problem solvers.

What is the sum?

The sum refers to the sum of numbers added together. It is the total of the summation, the addition of two or more numbers, or addends. For example, 8 + 3 = 11.

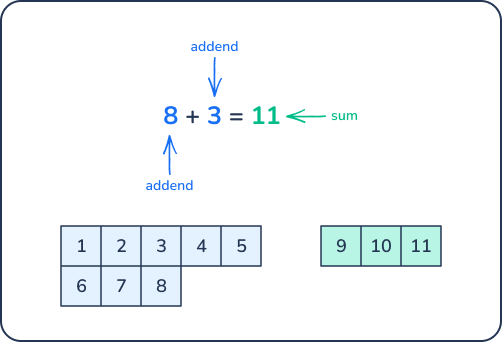
To find the sum of a math equation, there needs to be addends. An addend is the number that is added to another. For instance, in the above number sentence, 8 and 3 are the addends and the sum or total is 11. The mathematical symbol for addition is the plus sign, or +.

Learners first experience the mathematical operation of addition in kindergarten. They act out, model and draw pictures to show addition as putting two different objects together or adding two of the same objects together. Usually, learners start addition with number bonds and fact families to 10.

Teaching addition becomes more complex when students are introduced to expressions and abstract representations.

By fifth grade, students have seen the sum of an equation with whole numbers, decimals and fractions.

Students must have concrete, real life experiences that indicate addition to help solidify understanding. Understanding addition is not about keywords but about key ideas. When students understand the actions of addition to find the sum, they will better understand the mathematics behind it.

Finding the sum on a number line

One teaching strategy to help learners understand how to find the sum is to model the addition process on a number line.

A number line allows visualization of addition as adding one addend to another while also providing flexibility when decomposing an addend.

Here’s an example of a number line used in elementary education:

Grades K-1

In grades K-1, students are first exposed to a number path within 20. This number path supports one-to-one correspondence and the idea that numbers come before and after other numbers.

Students first use the number path to add within 20. For example, students can find the sum of 8 + 8 on the number path. If a student cannot identify the number 8, the student can use 1:1 counting to find 8. Then, the student must count forward the value of the second addend, which is also 8. After counting forward 8, wherever the student lands is the sum, In this case, 16.

As learners’ knowledge of addition progresses, students may transition to using a hundred chart to add two-digit and two-digit numbers, with one addend being a multiple of 10.

For example, students can use a hundreds chart to help them find the sum of 45 + 20.

1. First, locate the addend 45 on the hundreds chart.
2. Decompose 20 into two tens.
3. Jump 10 from 45 to land on 55
4. Then jump the second 10 to land
5. The sum of 45 + 20 is 65.

This strategy requires students to rely on place value strategies to support their additive thinking, or the use of place value charts.

When decomposing numbers and using the part-whole model, subitizing can help students to find the sum.

Grades 2-5

As students gain more experience with a number line, they explore open number lines. This tool allows them the flexibility of starting their addition process with any number and jump intervals on the number line can be made in tens, ones, even numbers or odd numbers.

Any value a student chooses is appropriate. There is not one specific, correct way to decompose or represent jumps on the number. As long as there is a starting point (one addend), and all parts of the second addend are added on, this strategy will work!

This method requires learners to break apart one addend to add it in parts. For example, 35 + 66 = ?

• Step 1: Choose one of the addends as a starting value on the number line: 35
• Step 2: Decompose the second addend into tens and ones: 66 = 60 + 5 + 1
• Step 3: Jump the intervals on the number line: 35 + 60 + 5 + 1 = 101

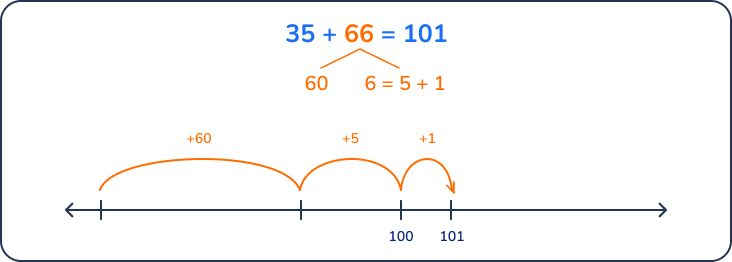
Although this example adds the larger addend to the lesser addend, younger children may find it easier to start with the larger addend on the number line and add the lesser value to find the sum.

While this method can be used for whole numbers, fractions and decimals, students must have secure place value knowledge.

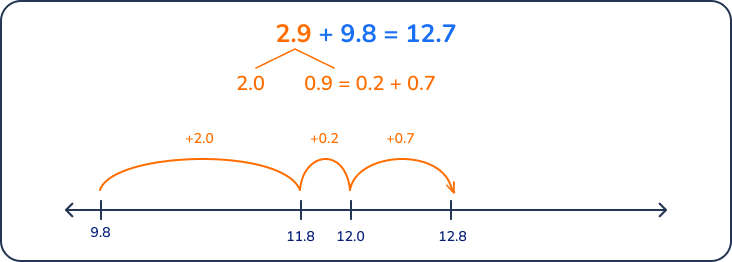
Finding the sum of decimal numbers using a number line example: 2.9 + 9.8 = ?

• Step 1: Choose one of the addends as a starting value on the number line: 9.8
• Step 2: Decompose the second addend into tens, ones, tenths and hundredths: 2.9 = 2 + 0.9
• Step 3: Jump the intervals on the number line: 9.8 + 2 + 0.9 = 12.7

What is the sum? Advanced concepts and techniques

Higher mathematics also uses the concept of the sum in topics such as money, arithmetic sequences, and natural numbers.

Here’s a deeper dive into how students can use the sum with these advanced concepts, and techniques and formulas to help find the sum.

Finding the sum of money or currency values

The sum of money is the total amount that results from compounding the initial principal. Students can use the following formula:

A = P (1 + \frac{R}{100})^{n}

A = amount

P = principal

R = rate

n = time in years

This formula calculates the interest before taking out a loan or putting money in a savings account. It shows exactly how much the interest will grow over time. Let’s take a look at an example together!

Example: The sum of money becomes $3,602 in 2 years at a compound interest rate of 4% per year. Find the sum of money at the beginning to the nearest hundredth.

Based on this example, here is the information we know:

A = amount = $3,602

P = principal = ?

R = rate = 4%

n = time in years = 2

Learners can apply this information to the sum of money formula.

\begin{aligned} 3,602 &= P (1 + \frac{4}{100})^{2} \\\\ 3,602 &= P (\frac{104}{100})^{2} \\\\ 3,602 &= P (\frac{26}{25})^{2} \\\\ 3,602 &= P (\frac{626}{625}) \\\\ 3,602 \times 625 &= P (\frac{626}{625}) \times 625 \\\\ 2,251,250 &= P \times 626 \\\\ \div 626 \quad & \quad \div 626 \\\\ \$3,596.25 & = P \\\\ \end{aligned}

Finding the sum of an arithmetic series

An arithmetic sequence is a list of numbers with a definite pattern or constant. For example, the arithmetic sequence below:

3, 6, 9, 12, 15, 18, 21…

The first thing to notice is that this set of numbers is all odd numbers. At a second glance, you may notice that if you take any number in this sequence and subtract the previous value from it the total amount will always be the same: 3.

That means 3 is the constant and this is an arithmetic sequence. The constant can either be:

• Positive: increasing arithmetic sequence
• Negative: decreasing arithmetic sequence

The sum of an arithmetic series formula is used to calculate the sum of all the terms within an arithmetic sequence. To find the sum of an arithmetic series, students may use the formula:

 S_{n} = \frac{n(a_{1} + a_{n})}{2}  

 S_{n}   = the sum of the arithmetic sequence

 a_{1}   = the first term

n = the total number of terms in the sequence

 a_{n}  = the last term of the sequence

Example: Find the sum of the arithmetic sequence 2, 5, 8, 11 up to the 20th term.

Before students can find the sum of the arithmetic sequence, they must first find the value of the 20th term in the sequence. To do that, they must use the formula for an arithmetic sequence:

 a_{n} = a_{1} + (n-1)d

 a_{n}  = the last term of the sequence

 a_{1} = the first term

n = the total number of terms in the sequence

d = constant or common difference

We know that the first term,  a_{1} , is 2, the total number of terms or n is 20, and the constant or common difference, d, is 3. Let’s use that information to solve for the 20th term.

\begin{aligned} a_{20} &= 2 + (20-1)3 \\ a_{20} &= 2 + (19)3 \\ a_{20} &= 2 + 57 \\ a_{20} &= 59 \\ \end{aligned}

Knowing the value of the 20th term, students can use it to help them find the sum of the arithmetic sequence.

\begin{aligned} S_{n} &= \frac{n(a_{1} + a_{n})}{2} \\\\ S_{n} &= \frac{20(2 + 59)}{2} \\\\ S_{n} &= \frac{20(61)}{2} \\\\ S_{n} &= \frac{1,220}{2} \\\\ S_{n} &= 610 \end{aligned}

Finding the sum of the first n natural numbers

Numbers can be classified into different types, for example:

• Whole numbers
• Integers
• Real numbers
• Decimals

Each type of number has a different set of properties and usage. One type of number that can be used to find a sum is natural numbers.

Natural numbers are positive, whole numbers from 1 to infinity, not including zero (i.e. 1, 2, 3, 4, 5 , etc.) To find the sum of natural numbers students can use the arithmetic formula shown below:

\text{Sum of natural n numbers } = (\frac{n(n+1)}{2})  

For example: Find the sum of the first 30 natural numbers.

This requires using the sum of natural numbers of formulas where the n terms is 30.

\text{Sum of natural n numbers } = (\frac{n(n+1)}{2})  

\begin{aligned} S_{n} &= (\frac{30(30 + 1)}{2}) \\\\ S_{n} &=( \frac{930}{2}) \\\\ S_{n} &= 465 \end{aligned}

What is the sum? Worked examples

Example 1:  Grade 2/3

The bagel shop sold 112 bagels on Monday. They sold 184 more bagels on Tuesday. How many bagels were sold in all?

Answer: 296

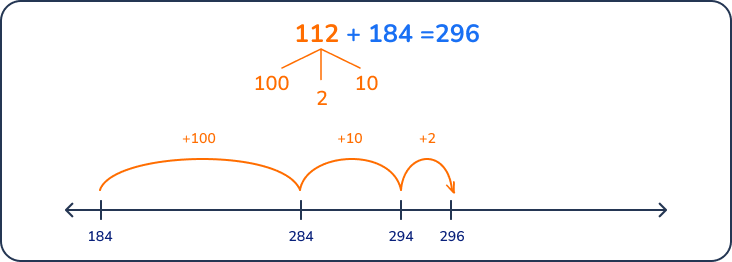
Example 2:  Grade 5

Ben found $2.75 when clearing out his room and found $4.09 when cleaning out his car. How much money did Ben find in all?

Answer: $6.84

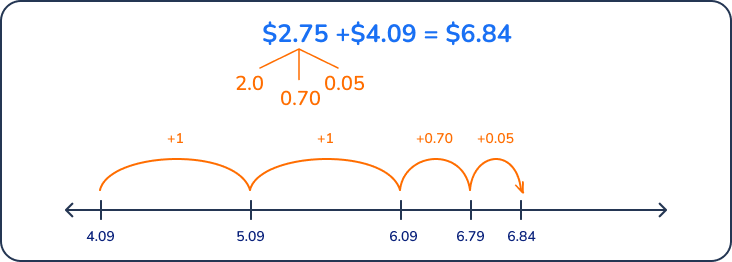
Example 3:

1. Find the sum of the arithmetic sequence 6, 11, 16, 21 up to the 30th term.

Answer:

\begin{aligned} a_{30} &= 6 + (30-1)5 \\ a_{30} &= 6 + (29)5 \\ a_{30} &= 6 + 145 \\ a_{30} &= 151 \\ \end{aligned}

1. Now that you have the value of the 30th term, find the sum of the arithmetic sequence.

Answer:

\begin{aligned} S_{n} &= \frac{n(a_{1} + a_{n})}{2} \\\\ S_{n} &= \frac{30(6 + 151)}{2} \\\\ S_{n} &= \frac{30(157)}{2} \\\\ S_{n} &= \frac{4,170}{2} \\\\ S_{n} &= 2,355 \end{aligned}

Example 4:

Find the sum of the first 17 natural numbers.

Answer:

\text{Sum of natural n numbers } = (\frac{n(n+1)}{2})  

\begin{aligned} S_{n} &= (\frac{17(17+1)}{2}) \\\\ S_{n} &=( \frac{306}{2}) \\\\ S_{n} &= 153 \end{aligned}

What is the sum? Practice problems

Practice Problem 1

There were 140 flowers in the flower shop. 93 more flowers were purchased. How many flowers are there altogether?

Answer: 233 flower

Practice Problem 2

Henry is planning a family trip. Here are some of the places he and his family would like to visit and the distance the cities are from their home:

City	Distance from home
Charlotte, NC	118.86 miles
Miami, FL	369.58 miles
Memphis, TN	311.62 miles
Montgomery, AL	131.80 miles
Lexington, TX	251.46 miles

If Henry’s family drives to Montgomery, AL  and home, how far was the trip?

Answer: 263.60 miles

Practice Problem 3

Find the sum of the arithmetic sequence 23, 29, 35, 41 up to the 17th term.

Answer: 1,207

Practice Problem 4

Find the sum of the first 28 natural numbers.

Answer: 406

Let’s “sum” it all up!

In mathematics, the sum is the total obtained by adding two or more numbers together. Learners first experience this concept in kindergarten by acting out and modeling the actions of addition.

As a learner’s experience increases, they begin to find the sum through pictorial strategies such as a number line. Students can use this tool with whole numbers, fractions and decimals.

The concept of a sum is applied in higher mathematics concepts such as arithmetic sequences with given numbers and natural numbers. Students must build a secure understanding of the sum in elementary and middle school to help them understand the concept of the sum in various mathematical applications.

Where possible, educators should use real-world mathematics problems and word problems to help learners find the sum as it allows them to become problem solvers.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?