What Is Subitizing? Explained For Elementary School Teachers
Subitizing is an essential part of developing number sense in young children. In this post, we explain what subitizing is, how it might look in the classroom or at home and why it is important for developing math skills.
What is subitizing?
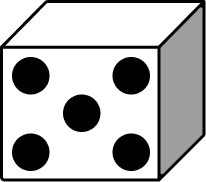
Subitizing is the ability to look at a small set of objects and instantly know how many there are without counting them. For example, when rolling a die we don’t need to count the dots to know what we have rolled. Subitizing was first coined by theorist Piaget. It is important in the early development of number sense.
There are two types of subitizing:
- Perceptual subitizing
- Conceptual subitizing
Perceptual subitizing
Perceptual subitizing is instinctive: we are able to look at the objects and just know what the number is without any further thinking. Children and adults alike are generally able to perceptually subitize smaller numbers up to 5.
Conceptual subitizing
Conceptual subitizing is the ability to look at a number of objects as a combination of smaller amounts. Looking at the die example again, when we roll a 6 we do not instinctively know it is 6. Instead, we see two groups of 3, meaning there must be 6.
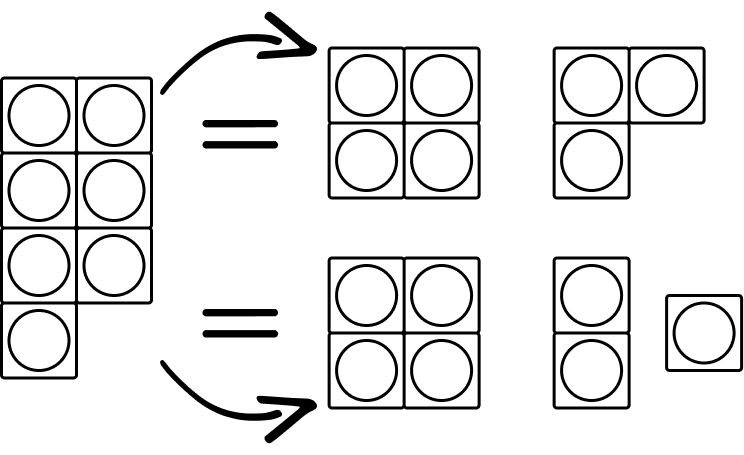
Numbers can be grouped in different ways. For example, the number 8 can be interpreted by combining numbers like 3 + 5 or 4 + 4. Developing conceptual subitizing skills is therefore an important step towards many other areas of math.
When do children learn about subitizing?
Subitizing is generally introduced during the early stages of elementary education.
During these early years, the focus is on developing foundational math skills, and subitizing plays a role in developing children’s number sense and understanding of quantity. Learners are exposed to different visual arrangements of objects (fingers, dice patterns, dots, etc.) and are taught how to quickly recognize the number of objects without counting them one by one.
Subitizing helps students develop a strong sense of numbers, which is essential for later math concepts.
How does subitizing relate to other areas of math?
Subitizing is an important skill to develop in the early years of math, as it is a core stepping stone to other areas of numeracy.
By encouraging young children to deepen their number sense, they gain a stronger understanding of how a number is made. This turns an abstract concept into something more meaningful.
For example, 7 is not simply 7. 7 is in fact 1 + 6, 2 + 5, 3 + 4, and so on. It can even be broken down further, for example 1 + 2 + 4.
Why is it important for children to learn about subitizing?
By understanding how a number is made, children can then learn basic number bonds up to 10, meaning the pairs of numbers that add together to make 10, for example. 1 + 9, 2 + 8, 3 + 7, and so on.
This understanding also acts as a springboard to other concepts such as part-whole, which will help children when they learn part-whole models and bar models in elementary school.
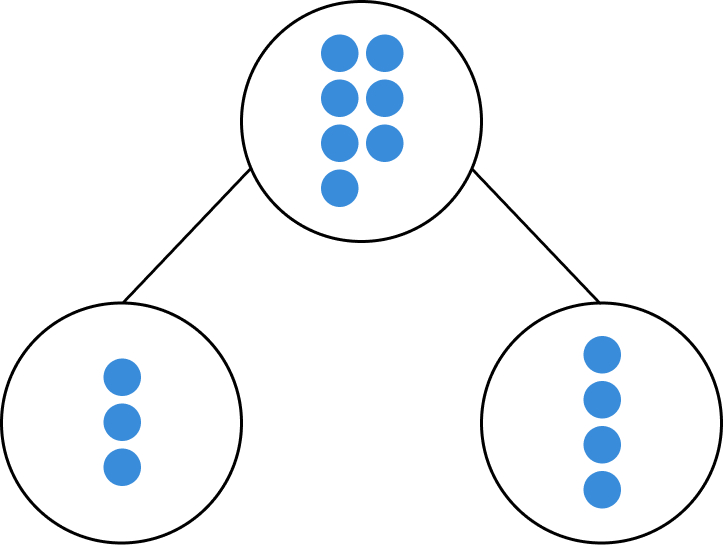
Subitizing is intrinsically linked to addition and subtraction. By first looking at addition, conceptual subitizing demonstrates to children that addition can happen in any order and that it is commutative.
For example, 4 + 5 = 9 and 5 + 4 = 9.
Once they are more fluent in addition facts, children can recognize the inverse relationship with subtraction. Both of these skills require fluency in conceptual subitizing, which in itself requires strong perceptual subitizing ability.
These simple addition and subtraction facts support children through elementary school where formal written methods are introduced.
Column addition and subtraction methods both require strong number knowledge. This way, children’s working memory is not taken up by simple arithmetic. Instead it can be used for regrouping and exchanging within the calculation and applying other reasoning and problem solving skills.
How to teach subitizing
Here are some ideas for exploring subitizing in your classroom, or even at home. Using concrete resources is key, as it enables children to physically explore the numbers before absorbing the abstract knowledge into their long term memory.
Groups of objects
Asking children to identify how many objects they can see without counting is one of the simplest ways to introduce subitizing. Objects could range from counters to cubes, or even to toy animals and dinosaurs.
You could also incorporate it into your outdoor learning, using groups of pebbles or making tallies out of sticks. After working on perceptual subitizing up to 5, you could begin asking children if they can combine groups of objects, starting simple with 1 + 2.
Dominoes
The dot patterns on dominoes are some of the most universally well-known examples of subitizing that we are exposed to in our lifetimes. Playing dominoes in small groups can help children become more fluent in these number patterns and quicker in their subitizing ability. Why not make it even more exciting for your class by playing with giant outdoor dominoes?
Dot patterns
Linked to dominoes but less uniform in their layout, dot patterns can further develop subitizing skills. Children can be challenged to identify the number without counting and identify different dot patterns that show the same amount. Children can try finding the odd one out.
Hands
Looking at fingers on hands is one of the most straightforward ways to start subitizing. Perceptual subitizing can be practiced with 5 fingers on one hand, while conceptual subitizing can be introduced by using all 10 fingers. For example, 6 fingers is one finger more than 5 fingers.
Flashcards
Pre-K children can be shown representations of numbers on subitizing cards, whether it be dot patterns or pictures of objects. Showing them the flashcard and then hiding it or turning it over can ensure children are prevented from counting the items and must actually use instantaneous subitizing.
Subitizing games
There are a number of ways games can be played in small groups to build subitizing skills. This may include playing simple board games that use a die, such as chutes and ladders. Playing with two dice can deepen children’s understanding further. Other games include snap and matching pairs, where various visual representations of numbers can be used in conjunction with number figures.
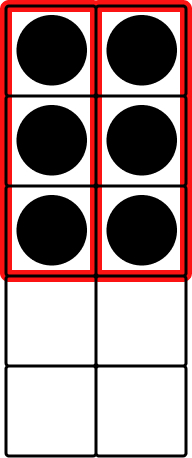
Tens frames
Common classroom resources such as ten frames can encourage children to combine groups of numbers and develop conceptual subitizing. Ten frames in particular can help children to see pairs of numbers. These can be easily reproduced at home by drawing the outlines on pieces of card and cutting them out.
3 examples of subitizing in math
Children in Pre-K can work through to develop their number sense. Working in small groups can expose children to other children’s thought processes.
1. Dominoes
Ask: What numbers can you see? Can you see any other numbers inside the number?
Answers may range from 7 to 3 and 4. You can encourage children to think deeper by asking them to spot pairs of 2 within the number, for example.
2. Colored number patterns
Ask: How many numbers can you see in this whole number?
Children may give different answers. For example, ‘I see 5 yellow, 2 green and 1 blue. There are 8 altogether’. Alternatively they may group them by position (2 + 2 + 4 = 8).
3. Subitizing to 10
Ask: How many numbers can you find in 10?
Using a 10 frame, you can ask children to show what numbers they can see. They may give different answers that begin to embed number bonds. You can challenge them to find as many numbers inside 10 as possible.
It is the ability to look at a small set of objects and instantly know how many there are without counting.
Rolling a dice is an example of subitizing. We don’t need to count the individual dots to know what the number is, we just instinctively know.
The two types of subitizing are perceptual and conceptual. Perceptual subitizing is instinctive (you just know from looking) whereas conceptual requires more thought. For example, when looking at the number 6 on a die, we actually see two groups of 3 to know that there are 6.
Subitizing works for small numbers. We are able to perceptively subitise numbers up to 5, beyond this we use further mental calculation and move into conceptual subitizing.
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Why not learn more about how it works?
The content in this article was originally written by primary school teacher Rosie Hasyn and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.
