What Is Estimation In Math: Estimating Numbers Explained For Teachers, Parents and Kids
Estimation in math is an important process taught from 2nd grade. It encourages children to have a good understanding of the magnitude of numbers rather than overly relying on mathematical procedures to achieve an answer.
4th Grade and 5th Grade End of Year Math Assessments
Assess math progress for the end of grade 4 and grade 5 or prepare for state assessments with this free resource
Download Free Now!What is estimating in math?
Estimating in math is a way of approximately calculating an answer (getting a ‘rough answer’) or to check its accuracy (the ‘right answer’). You shouldn’t need to use a calculator or any written methods when estimating, even with large numbers or decimal numbers.
Estimating numbers will always require you to use mental math skills and also skills from rounding numbers in one way or another.
Examples of estimating calculations
A pencil costs 98 cents and you want to buy 29 – one for each child in the class. You would estimate that this would cost $29.
A bottle of juice holds 2 liters and you want to share it amongst 8 friends. You could estimate, by eye, that each friend could get half a glass each (this obviously depends on the capacity of the glass!)
When do children learn about estimating in the national curriculum?
Schools following Common Core math
2nd grade:
- estimate lengths using units of inches, feet, centimeters, and meters.
3rd grade:
- tell and write time to the nearest minute and measure time intervals in minutes.
- solve word problems involving addition and subtraction of time intervals in minutes, e.g., by representing the problem on a number line diagram.
- measure and estimate liquid volumes and masses of objects using standard units of grams (g), kilograms (kg), and liters (l).
4th grade:
- select and accurately apply appropriate methods to estimate or mentally calculate products.
- select and accurately apply appropriate methods to estimate and mentally calculate quotients, and interpret remainders based upon the context
5th grade:
- develop fluency in calculating sums and differences of fractions, and make reasonable estimates of them
- use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers.
- develop fluency in adding and subtracting of decimals to the hundredths, and make reasonable estimates of their results
- use estimation to check answers to calculations and determine, in the context of a problem, an appropriate degree of accuracy
Other schools:
Depending on the state curriculum or standards your child’s school uses, estimation may be taught in different grade levels at different times. Schools that follow the Texas State standards, or TEKS, estimation begins in 3rd grade with rounding to the nearest 10 or 100 to estimate solutions to addition and subtraction problems.
It continues in 4th grade with rounding to the nearest 10, 100, or 1,000 to estimate solutions involving whole numbers. In 5th grade, students are expected to estimate to determine solutions to mathematical and real-world problems involving addition, subtraction, multiplication, or division.
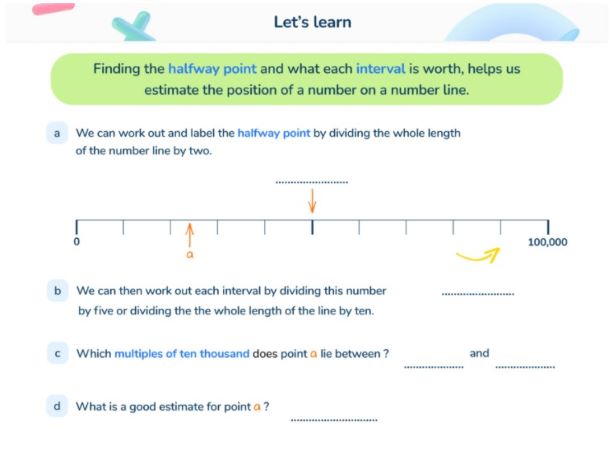
How does estimating relate to other areas of math?
As mentioned above, estimating is referenced throughout the Common Core State Standards in a variety of topics: using the four operations, measurement and geometry.
Estimating in real life
We use estimating every day in real life – probably without even noticing. If you are buying a packet of chips for $.99 cents and a drink for $1.99, you would estimate the total cost to be around $3 (the exact answer would be $2.98).
You might be considering refilling your car with gas, but if you know how many miles per gallon your car drives, and how much gas you have left, you might be able to estimate how far you can go before refilling.
Estimating is also often used in professional contexts such as in project planning and product development.
3 worked examples for estimating in math
1. Estimate the answer to 3.39 + 5.52.
Estimation questions (especially those without context) often don’t specify the degree of accuracy required in the estimation. The further away we round to, the less accurate we will be.
For example, numbers with 2 decimal places like these could be rounded to 1 decimal place (3.4 + 5.5) to give us an approximate answer of 8.9.
However, they could also be rounded to the nearest whole number (3 + 6) to give us an approximate answer of 9.
The real answer is 8.91.
Rounding to 1 decimal place gave us a more accurate answer, but was arguably a slightly more complex calculation mentally, whereas rounding to the nearest whole number gave us a less accurate answer, but made simplifying the mental calculation easier.
2. A phone costs $578.92, but there is a 40% discount. Approximately how much does it cost now?
The word ‘approximately’ is used to mean estimation. As previously mentioned, the amount here could be rounded to $578.90, $579, $580 or $600 – again, the further away it’s rounded, the less accurate the answer will be.
However, looking at the four options we have here and taking the context of the problem into account – money – we could logically conclude that using the last option would be the most straightforward, especially when working with percentages.
40% of $600 is $240, so the phone’s new approximate cost or cost estimate can be calculated using subtraction: $600 – $240 = $360. (The real answer is $347.35, so our approximate answer was a good estimation.)
As you can see, word problems will often require the student to consider what the better estimate to use would be.
3. Use rounding to estimate a sensible answer to 120,107 x 61.
120,107 rounds to 120,110 or 120,100 or 120,000 or 100,000.
Of the first four options, the third – 120,000 – would be the best estimate to use as not only is it one of the easiest to multiply by 60 (which is what 61 rounds to) mentally, but it would give a more accurate answer than choosing 100,000. 120,000 x 60 = 7,200,000 (times table knowledge can be used here as 12 x 6 = 72).
5 estimating in math practice questions and answers
1. Taylor wants to estimate the answer to this calculation involving fractions:

Answer: 4 – 2 + 2
2. To find the approximate total of 3.2 + 5.9, which two whole numbers would you add together?
Answer: 3 + 6
3. Megan walks 3,102m on Monday, 4,989m on Tuesday and 2,050m on Wednesday. Approximately how many meters has she walked altogether?
Answer: 3,000m + 5,000m + 2,000m = 10,000m
4. Round 53,892 to the nearest thousand to estimate the answer to 53,892 ÷ 6.
Answer: 54,000 ÷ 6 = 9,000
5. Estimate 532 × 12 to help you to identify which of the following is the actual answer to the calculation: 638; 6,384; 63,840; 1,596
Answer: 530 x 10 = 5,300 which is closest to 6,384
FAQs
Estimating in math requires a strong knowledge of rounding as that is often the best way to ensure you don’t make a mistake in your estimation.
For example, if asked to estimate the answer for 0.7 x 0.8, by rounding the decimals and then multiplying (0.7 and 0.8 both round up to 1, and 1 x 1 = 1) you are better able to check the accuracy of the answer (5.6 is much larger than 1, so the multiplication could be recalculated to achieve 0.56, which is much closer to 1).
Firstly, establish how accurate the estimate needs to be (to the nearest cent? Tenths? Hour? Pound? Kilometer?). Next in the estimation process would be to round the numbers up or down, depending on the context of the question.
Estimating is a way of getting a ‘rough answer’ by using rounding. You shouldn’t need to use a calculator or any written methods when estimating.
Wondering about how to explain other key math vocabulary to children? Check out our Elementary Math Dictionary for Kids and our What is Math Mastery? blog to help with lesson planning and at home math revision.
You can find plenty of printable estimating worksheets, numeracy worksheets and plenty of other learning resources for primary school students on the Third Space Learning Math Hub.
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Why not learn more about how it works?
The content in this article was originally written by primary school teacher Sophie Bartlett and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza





