What Is Rounding in Math: Rounding Numbers Explained for Teachers, Parents and Kids

Here you can find out about rounding numbers, why it is used, and how you can help children understand it. Rounding digits requires a solid understanding of place value. Students will need to be aware of the number of decimal places or significant figures a value has to go from that original number to a rounded number.

What is rounding in math?

Rounding numbers makes them ‘easier’ to use or understand while also keeping the number close to its original value. Instead of using exact numbers, simpler values can be used.

For example, 189.2 could be rounded to 189, 190 or 200, depending on the degree of accuracy required. In context, $19.99 could be rounded to $20; 56 minutes could be rounded to an hour.

Rounding to the nearest 10

Students first officially encounter this in 3rd grade. In order to round to the nearest 10, children must first understand what multiples of ten are (numbers in the ten times table, or numbers divisible by 10, e.g. 30, 250, 3430 etc.).

They must then be able to identify which multiples of 10 a given number is between, e.g. 218 is between 210 and 220 (a number line is often used for this, as seen below).

Finally, children should then identify the nearest multiple of 10 – in this case, 220. Children should round numbers up If they lie halfway between two multiples (and therefore end in a 5).

In this case, the number will always round up to the multiple of 10 above it.

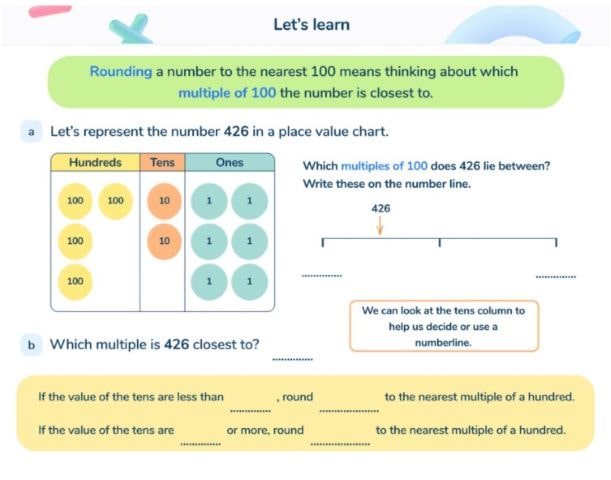
Rounding to the nearest 100 

Students first officially encounter this in 3rd grade. In order to round to the nearest 100, children must first understand what multiples of 100 are (numbers in the 100 times table, or numbers divisible by 100, e.g. 500, 2500, 34300 etc.).

They must then be able to identify which multiples of 100 a given number is between, e.g. 218 is between 200 and 300 (a number line is often used for this).

Finally, children should then identify the nearest multiple of 100 – in this case, 200. If a number lies halfway between (and therefore ends in 50), the number will always round up to the multiple of 100 above it.

Rounding to the nearest integer or whole number 

Students following Common Core State Standards first officially encounter this in 5th grade. Children must be able to identify which whole numbers, also termed ‘integers’, are either side of a decimal number.

For example, 6.2 is between 6 and 7; 14.92 is between 14 and 15 (again, a number line is a useful tool in helping to visualize this).

They should then work out which of these integers is closer to the decimal number using the numbers to the right of the decimal point.

As before, if the decimal number is exactly halfway between two integers (such as 3.5), it will always round up to the integer above it (in this case, 4).

Rounding to the nearest tenth

Students first officially encounter this in 5th grade. In a similar fashion to the methods previously explained, children should be able to identify the tenths either side of a decimal number.

For example, 4.62 is between 4.6 and 4.7; 5.213 is between 5.2 and 5.3.

Sometimes these decimal numbers could be written with a 0 in the hundredths place and/or thousandths place value to make it easier to work out the surrounding tenths: in the first example above, 4.62 has 62 hundredths and is therefore between 60 hundredths (4.60, or 4.6) and 70 hundredths (4.70, or 4.7).

Finally, children should then work out which of these tenths is closer to the decimal number. As the nearest hundredth of 4.62 is 60, the nearest tenth is will be 6.

Once again, if the decimal number is exactly halfway between two tenths (such as 2.75), it will always round up to the tenth above it (in this case, 2.8).

When do children learn about rounding numbers in elementary school?

Schools following Common Core:

In 3rd grade children are taught to:

• Round any number to the nearest 10 or 100.
• Assess the reasonableness of answers using mental computation and estimation strategies including rounding.3

This progresses to 4th grade, where students are expected to:

• Use place value understanding to round whole numbers to any place.
• Assess the reasonableness of answers using mental computation and estimation strategies including rounding

And finally to 5th grade:

• Use place value understanding to round decimals to any place. 

Other schools:

Depending on the state curriculum or standards a school is using, rounding may be taught in different grade levels. If your child is in a district that follows the Texas Essential Knowledge and Skills, rounding to the 10s and 100s begins in 3rd grade, rounding to the nearest hundred thousand is taught in 4th grade, and rounding decimals to the nearest tenth and hundredth is introduced in 5th grade.

How does rounding numbers relate to other areas of math?

Rounding is used to estimate and check answers to problems.

For example, when multiplying decimals (such as 0.7 x 0.8), students may misinterpret the magnitude of the answer (in this case, perhaps 5.6).

Rounding the decimals and then multiplying (0.7 and 0.8 both round to 1, and 1 x 1 = 1) helps to check the accuracy of the answer (5.6 is much larger than 1, so the multiplication could be recalculated to achieve 0.56, which is much closer to 1).

Rounding in math in real life

Rounding is useful in real life.  For example, rounding remainders appropriate to the context: 

• Rounding up: A mini bus holds 12 people and you need to transport 161 people. 161 ÷ 12 = 13.4, but you can’t have 0.4 of a mini bus, so you would need to round up to work out that 14 mini buses would be needed.
• Rounding down: An egg carton holds 12 eggs and you have 161 eggs to package. 161 ÷ 12 = 13.4, but you can’t have 0.4 of an egg carton and they all must be fully filled, so you would need to round down to work out that 13 egg cartons would be needed.

In the first example, 13.4 wouldn’t conventionally be rounded up, but in the context of the problem, it was required to be.

Here’s a fun real-life activity parents could get their children to do during their next trip to the grocery store: tell your child you have $15 to spend on fruit and vegetables and they need to determine how many items you could purchase by rounding up their prices to the nearest whole dollar. Find out how accurate their estimates were when you check out!

3 worked examples for rounding in math

1) Round 218 to the nearest multiple of 10.

Answer: 220

2) Round 42.4 to the nearest whole number.

Answer: 42

3) Round 1.15 to the nearest tenth.

Answer: 1.2 (any number that is halfway between always rounds up)

Once children are confident with the concept through using a number line, they may be able to round by just looking at two digits:

• When rounding to the nearest 10, you only need to look at the tens place (to identify if it will change or not) and the ones place (to identify if it will round the tens digit up or down) – e.g. in 3,268, the 8 rounds the 6 ‘up’ to a 7, becoming 3,270
• When rounding to the nearest 100, you only need to look at the hundreds digit (to identify if it will change or not) and the tens digit (to identify if it will round the hundreds digit up or down) – e.g. in 742,125, the 2 rounds the 1 ‘down’ to stay as 1, becoming 742,100
• When rounding to the nearest 1000, you only need to look at the digits in the thousands and hundreds place – e.g. in 42,517, the 5 rounds the 2 ‘up’ to a 3, becoming 43,000

… and so on.

5 rounding in math practice questions and answers

4th grade

Q: Circle the number which is closer to 1000 and explain how you know: 996, 1006

Answer: 996 is closer to 1000 as it is only 4 away, whereas 1006 is 6 away.

Q: Round 73,482 to the nearest: a) 10,000   b) 1,000   c) 100

Answer: a) 70,000   b) 73,000 c)   73,500

Q: Round 3,593,174 to the nearest million.

Answer: 4,000,000

5th grade

Q: John thinks of a whole number. He multiplies it by 4. He rounds his answer to the nearest 10. The result is 50. Write all the possible numbers that John could have started with.

Answer: 12 or 13 (Any number from 45 – 54 would be rounded to 50 when being rounded to the nearest 10. There are only two multiples of 4 within that range: 48 and 52. Dividing those by 4 gives you 12 and 13)

Q: Round each of these numbers to the nearest 100: a) 20,906   b) 2,090.6   c) 209.06

Answer: a) 20,900   b) 2,100   c) 200

FAQs

Wondering about how to explain other key math vocabulary to children? Check out our Math Dictionary For Kids and our What is Math Mastery? blog.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by primary school teacher Sophie Bartlett and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.