What Is The Lowest Common Multiple: A Guide For Elementary School

In this post we will be answering the question “what is the lowest common multiple?” and providing you with all of the information you need to help elementary school children understand this area of math. We’ve also got some questions based around the lowest common multiple that children can complete, all to help them master math fast!

What is a multiple in math?

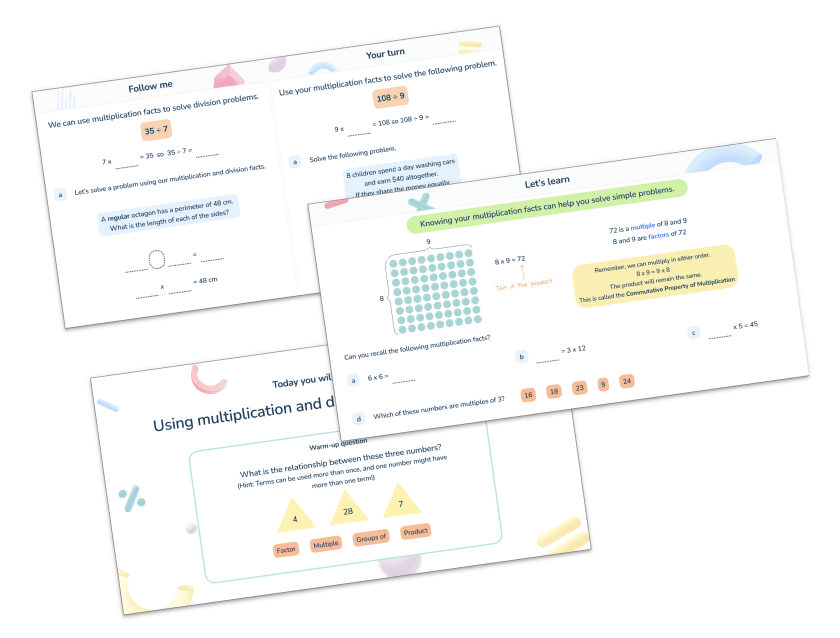
A multiple is a number that can be divided without any remainder. 

Sometimes it helps children to think of it as a number in another number’s multiplication table – for example, 24 is a multiple of 12; it is also a multiple of 1, 2, 3, 4, 6, 8, and 24. The first five multiples of 6 are 6, 12, 18, 24 and 30.

Multiples and factors link together – for example, 4 is a factor of 12 and 12 is a multiple of 4.

See also: Divisibility rules

What is a common multiple in math?

A common multiple is a multiple that is shared by two or more numbers. 

12 is a common multiple of 6 and 4 as it’s in both the 6 and 4 times tables. 

Three common multiples of 6 and 9 are 18, 36 and 54.

What is the lowest common multiple?

The lowest common multiple is the lowest multiple shared by two or more numbers. 

For example, common multiples of 4 and 6 are 12, 24 and 36, but the lowest of those is 12; therefore, the lowest common multiple of 4 and 6 is 12. 

How to find the lowest common multiple

One way of helping children to find the lowest common multiple is to ask them to list the multiples of each number until they come across the first one each number shares. 

For example, the LCM of 5 and 7 is 35:

When do children learn about lowest common multiple?

Children are introduced to multiples in kindergarten (perhaps without knowing the actual term) when they may learn to count in multiples of twos, fives and tens, as part of their learning of number bonds and skip-counting. In 1st grade, students subtract multiples of 10 in the range 10-90 from multiples of 10 in the range 10-90.

In 2nd grade, children count within 1000; skip-count by 5s, 10s, and 100s.

In 3rd grade, students multiply by multiples of 10. They also learn the terms “multiple” and “factor” while studying their multiplication facts.

4th graders should be able to find all factor pairs for a whole number in the range 1-100. They should be taught to identify multiples and solve problems involving multiplication and division including using their knowledge of multiples.

Common multiples are not introduced until 5th grade. 5th graders are expected to use common multiples to express fractions in the same denomination and to solve problems involving unequal sharing and grouping using knowledge of fractions and multiples.

How do lowest common multiples relate to other areas of math?

Lowest common multiples are useful when needing to express fractions in the same denomination (required when adding or subtracting, ordering or comparing fractions). For example, to calculate 3/5 + 1/6, we’d need to find the common denominator by calculating the lowest common multiple of 5 and 6 (30). We can then convert the fractions to 18/30 + 5/30 = 23/30.

Wondering about how to explain other key math vocabulary to children? Check out our Math Dictionary for Kids, or try these math terms:

• What Is Long Multiplication: Explained For Teachers, Parents And Kids
• What Is A Cube Number: Explained For Teachers, Parents And Kids
• What Is A Square Number: Explained For Teachers, Parents And Kids
• What Is The Highest Common Factor: Explained For Teachers, Parents And Kids

Lowest common multiple practice questions

1) What is the lowest common multiple of 8 and 10?

2) Write all the common multiples of 3 and 8 that are less than 50.

3) What is the lowest common multiple of 100 and 50?

4) Write all the common multiples of 4 and 6 that are less than 60.

5) What is the lowest common multiple of 1000 and 650?