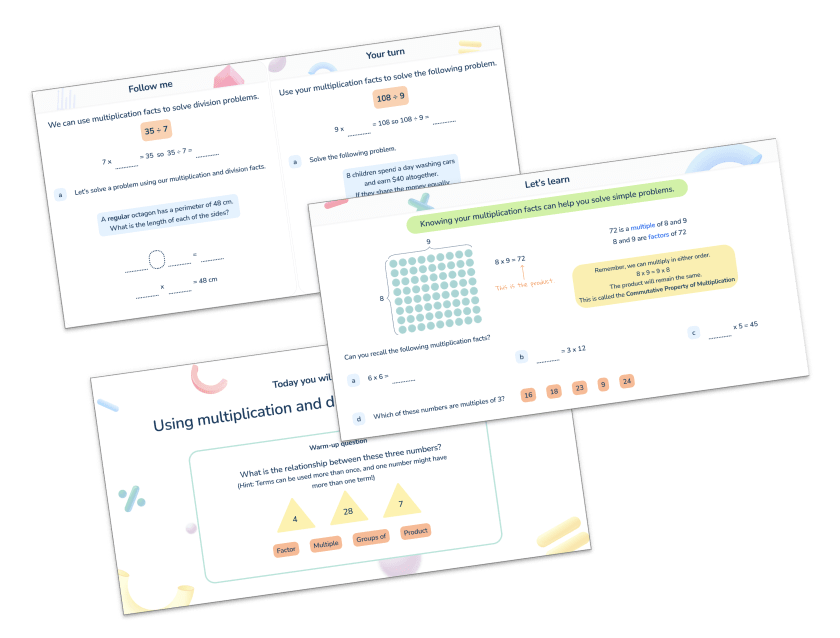
How to Teach Multiplication: Math Bootcamp
Want to know how to teach multiplication to elementary math students? You’ve found the right place! This post is part of our interventions bootcamp series: designed to support 4th and 5th grade teachers to achieve grade related expectations with students who need that extra intervention.
- The ‘How To Teach Elementary Math’ Interventions Bootcamp Series
- DIAGNOSIS: what are students’ key misconceptions in multiplication?
- Misconceptions & strategies for ‘Emerging’ in multiplication
- Misconceptions and strategies for ‘Developing’ in multiplication
- Misconceptions and strategies for ‘Securing’ in multiplication
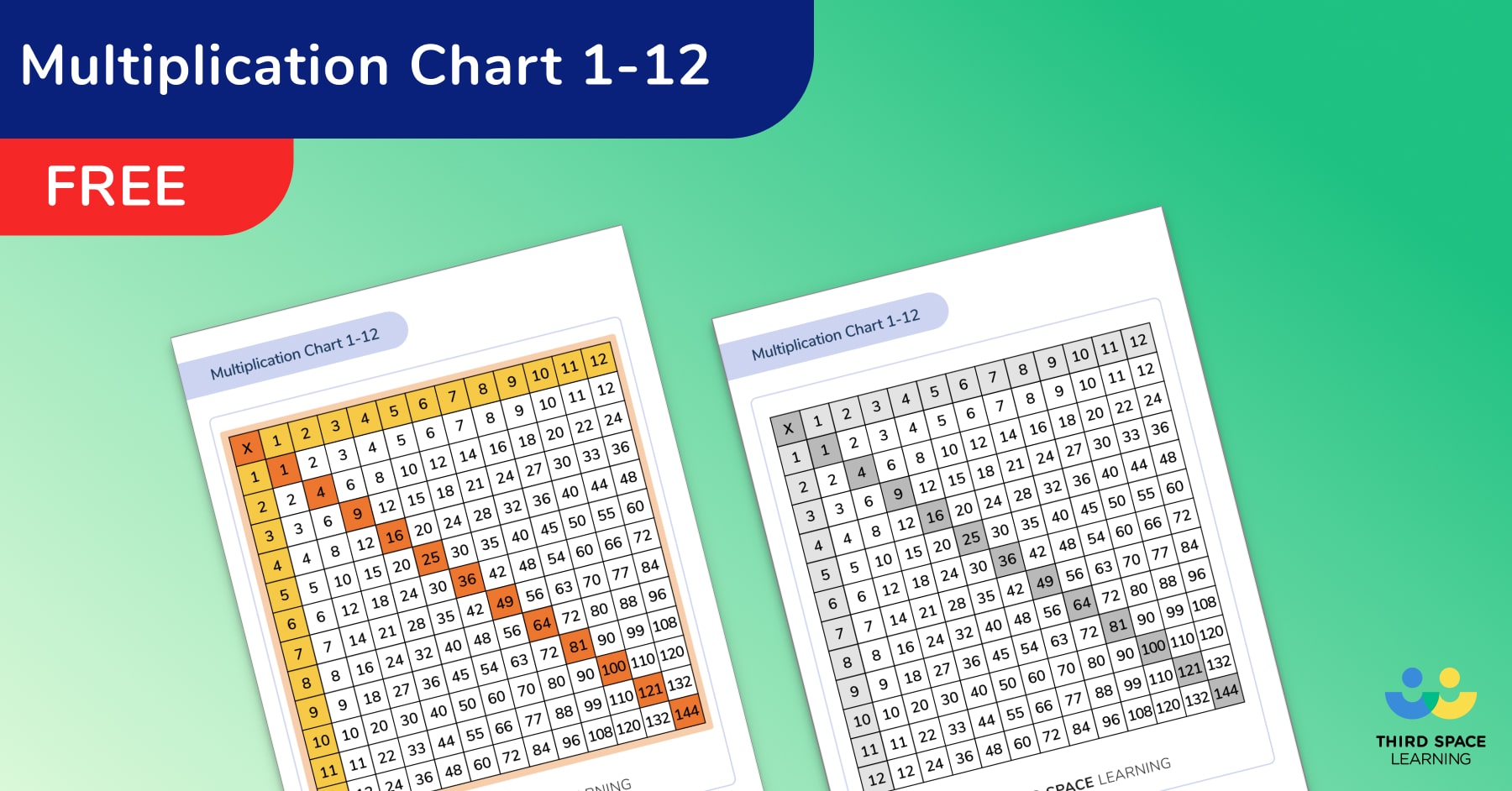
Multiplication Chart 1-12
A great way to spot patterns with times tables and learn about factors and multiples
Download Free Now!Moving swiftly on from algebra, the next bootcamp post is on multiplication. It seeks to help school leaders, math coordinators and upper elementary teachers diagnose where students are struggling with the basics of multiplication.
We then track back to different stages of understanding and provide strategies that can be used with whole classes, small intervention groups or alongside one to one interventions, such as those provided by Third Space Learning.
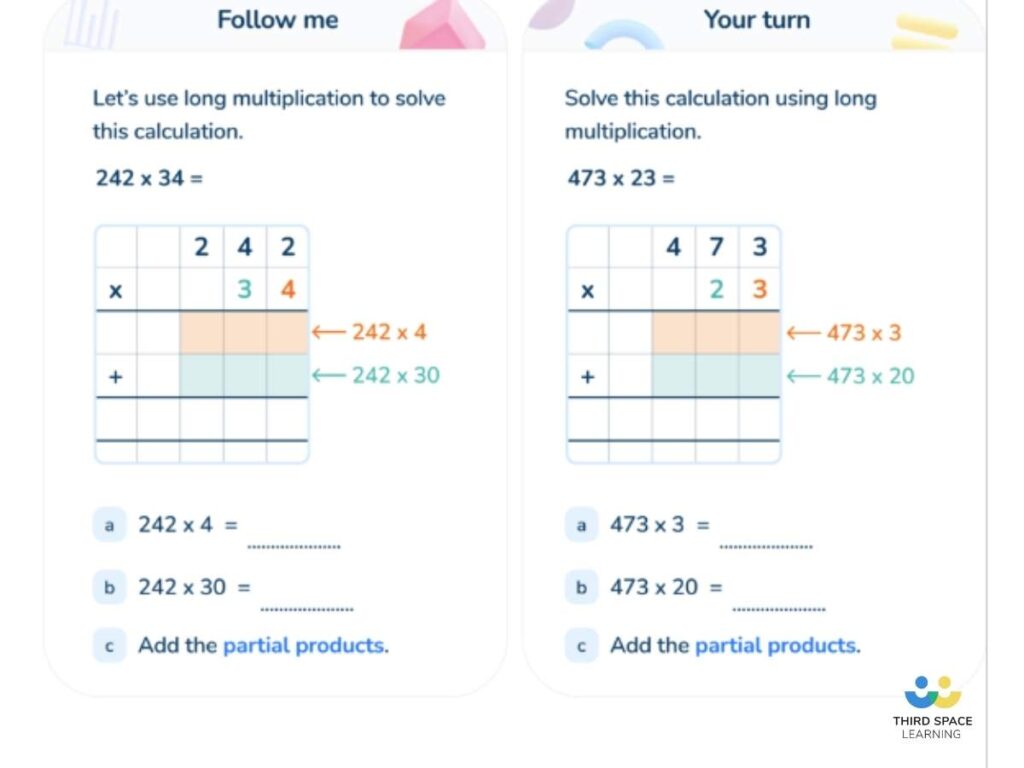
Each post follows a similar structure:
1. First, you’ll diagnose where students are struggling with the basics of that area of Math.
2. Next, you’ll track back to the different stages of understanding and examine what the misconception might be in detail.
3. Finally, we’ll give you strategies that can be used with whole classes, small groups or alongside one to one interventions.
The ‘How To Teach Elementary Math’ Interventions Bootcamp Series
- How to teach addition
- How to teach subtraction
- How to teach fractions
- How to teach place value
- How to teach algebra
- How to teach multiplication
- How to teach division
In this post on multiplication, we help you solve problems such as:
- Students keep making mistakes with their written methods…why?
- Why aren’t students using their multiplication charts to help them?
- My students are okay with arithmetic, but they can’t use their knowledge in other situations.

Meet Skye, the voice-based AI tutor making math success possible for every student.
Built by teachers and math experts, Skye uses the same pedagogy, curriculum and lesson structure as our traditional tutoring.
But, with more flexibility and a low cost, schools can scale online math tutoring to support every student who needs it.
Find out more
DIAGNOSIS: what are students’ key misconceptions in multiplication?
From the below students, find the best fit for those you are looking at. Then use this to guide where in the post to read for support:
Antoni has a rapid recall of most multiplication facts. He is able to use these in the written method, usually calculating 4 digit by 2 digit numbers correctly. However, Antoni struggles to apply his knowledge in problems where multiplication facts could help cut down his workload. Stage: SECURING.
Rachel can use some number facts within the written method of multiplication, although she frequently still uses her fingers to help her. Through time and repetition she has learned how to carry out the method but struggles with larger numbers such as four digit by two digit numbers. She often makes errors with the written method and with those larger calculations. Stage: EMERGING.
Jenny can recall most of her times tables and use them in the written method. She struggles at the larger-end with some errors in individual elements due to mixing up her columns. Jenny struggles to use her knowledge of multiplication for the inverse, particularly with long and short division problems where multiplication facts could support her. Stage: DEVELOPING.
Lewis finds recall difficult. He knows some number facts but not complete sets such as recall of the 3 times table. He has a small working memory and, even with concrete materials, doesn’t seem to grasp multiplication as arrays or repeated addition sufficiently to build on it. Stage: small group.
Lewis’ needs are beyond the scope of a small group or this post. He needs specifically targeted one to one support such as that provided by Third Space Learning to catch him up to a point where small group intervention could be considered.
Misconceptions & strategies for ‘Emerging’ in multiplication
1. Develop number facts
Without a secure understanding of multiplication facts, students like Rachel will continue to lack confidence and struggle when manipulating more in depth calculations.
Let the amount of time left teaching these students guide the extent of number fact development. You don’t want to end up slightly improving their number facts without filling in the significant other gaps that the children have, however you also want to ensure they develop their number fact fluency.
2. Secure foundations
It is key that these students understand what multiplication is, rather than purely learning to do a written method. If they understand what they are doing and why they are doing it, they will be much more successful when eliminating errors in complex written methods.
Briefly start with multiplication as repeated addition, showing groups of 8 with physical objects such as counters or unifix cubes, while also displaying a blank number line that gets filled in as you count the groups of counters with the student (8 + 8 + 8 + 8).
Quickly move on to showing the objects in an array form to show the commutativity of multiplication, which will support student’s application of multiplication in the written method and using and applying contexts (if they are prompted and links made at the time, to begin with).
3. Incorporate the area model method of multiplication
Once students fully understand these aspects of multiplication, we recommend that you introduce the area model method for multiplication as a bridge between physical approaches and the abstract written method. This will support their understanding of the process.
For information on this topic, read our blog post on how to use multiplication charts in your classroom.
Give students the calculation 38 x 7.
Using different colors for tens and ones, model using the area model method to partition the 38 into 3 tens and 8 ones (this is a key step as it will support the move to the written method). Explain this will help us carry out the multiplication as 30 x 7 added to 8 x 7 is a lot simpler than 38 x 7.
Ask students to calculate 3 tens multiplied by 7 ones. Watch for, and then guide, students to think of this as 3 (tens) x 7 rather than 30 x 7, again supporting the next move to the written method. Then they can think of their answer as 21 ‘tens’, shown by placing zero as a place holder in the ones (moving the answer to ‘tens’).
If needed, get students to draw this as two hundreds and 1 ten to deepen their understanding. Then the students calculate 8 ones x 7 ones. If they struggle with their 7 times table, they should be nudged to make earlier links with commutativity (arrays) and use their 8 times table.
Students should then be shown to use the written method in addition to add the two results together (210 + 56). Even if they can do this mentally, it will support an element of the written method.
Once the key elements above are understood (partitioning and calculating tens and ones separately, thinking of the number as 21 ‘tens’ rather than 210, and adding the totals using written addition), larger calculations can be examined. Here, base 10 blocks can be used to support struggling learners.
Now calculate 352 x 34. This will take some time using the grid method but it is an important step. Partition into 300, 50, 2 x 30, 4. Again, use colors for each sized digit and relate these to using colors in each calculation.
For each stage in the calculation, get the students to think about the size of the numbers they are adding which can be achieved by using drawings to represent the thousands (mini cubes), hundreds (squares), tens (diagonal lines) and ones (crosses).
Students then add up all totals together using a longer written addition like the one below. Discuss with students how this took a while and there is a quicker method we can look at to help us. They then should be able to explain what they know about the method (formal written method).
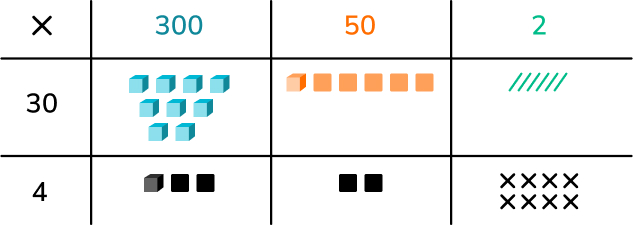
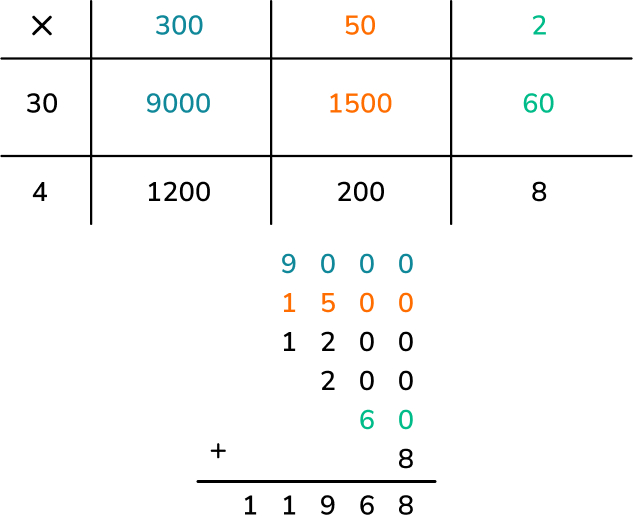
It is at this stage that students like Rachel and Jenny are ready to develop their fluency together.
Misconceptions and strategies for ‘Developing’ in multiplication
Standard Algorithm Multiplication
Unlike the area model method, the standard algorithm multiplication method is taught beginning in 5th grade. This means it’s more likely to be more recently in students’ memory, but also that it’s less likely to be fully embedded and understood by them. Therefore it may require more focus given to it to ensure comprehension.
As previously modeled with the area model method, take the same calculation and model the standard algorithm multiplication method alongside it. Explain that the main difference is how we compress each subtotal into the same column and use exchanging to do so (just as with written addition).
Initially focus on the layout, showing how the same process is being followed until students are clear with this. Then switch focus to the relative position of each calculation: i.e when calculating 3 hundreds multiplied by 3 tens, discuss what 3 hundred x 3 is (900). As such, to find out 3 ‘tens’ rather than 3 ‘ones’, it must be 10 times bigger than 900, which is 900 with an extra 0 as a place holder (9000).
Typically, this stage is difficult to explain without resorting to ‘adding zeros’ and also where students like Jenny and Rachel are likely going to struggle. Therefore, where necessary refer back to the same stages in the area model method. Try to ensure students are always explaining what they are doing, how they know, what the subtotals should be and why.
After a while, they should be able to refer to the previous example as 3 x 3 = 9 and then count the zeros (two in 300 and one in 30) concluding they need to move 3 positions larger because of this.
Once students are fairly secure here, they can be reintroduced to 4 digit by 2 digit calculations.
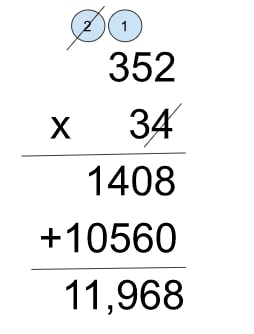
Division problems
Rather than being used as a separate element (as explained here) students who are not applying their knowledge of multiplication facts to long division problems should be constantly nudged to do so.
Many students who are not secure with recall of their tables will choose a formal written method. Indeed, even students that are confident with their multiplication facts may do so as they see it as ‘the right way’ or ‘the grown up way as we have been taught this more recently’.
Yet, it is crucial that students learn to be mindful and apply whatever method they think is the most efficient to any given situation, rather than the most recent one they have learned.
For example, when tackling a word problem that has 492 ÷ 12 at its core, students should be able to use their knowledge of place value to tackle this as 492 ÷ by 10 = 49.2. They then half this to give an answer of 24.6.
Equally, when tackling 390 ÷ 3, students should see 390 as 39 tens, and ‘we know that 3 fits into 39 thirteen times so 3 must fit into 39 thirteen times. So it fits into 390 one hundred and thirty times.
From this point on, students just need lots of practice of choosing the most efficient method (as they should have been doing throughout their math lessons) and applying it to using and applying contexts.
Misconceptions and strategies for ‘Securing’ in multiplication
Using and applying math techniques
Every school has at least one Antoni. Quick with recall and good with written methods. But do they apply the most efficient method when tackling problems? No, they often go for a mental strategy when they should have used a written method, making errors, or jump straight to a written method when it isn’t needed.
Here are 2 situations and examples with strategies that can be used whenever these issues arise with students like Antoni, whether in class or as a focused booster.
Situation 1- Applying in measures contexts
When calculating the area of a triangle, students will often leap straight away to ‘the method we have learned for this situation’.
While there is nothing wrong with this, we want them to go further and think of the best way to calculate it. Otherwise, they will simply use whatever they were taught with the method in question (in this instance, area of a triangle).
This will likely mean they leap straight to a formal written method when there may be a more efficient method.
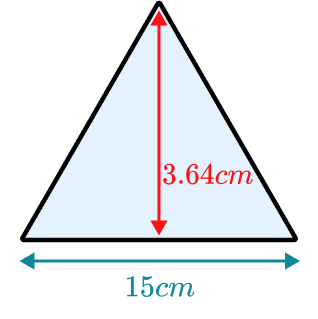
A quicker, more efficient method over using the standard algorithm for multiplication that would still minimize errors would be to mentally (with notes) calculate 3.64 x 10 = 36.4.
Students could then find half of this amount (18.2) and add it to 36.4 to give a total of 54.6cm. This would be significantly quicker to calculate over a 3 digit by 2 digit written method, potentially involving decimals.
But how do we get students to ‘see’ this?
We need to train them over time to be mindful and spend a few seconds (once they know what they are being asked to ‘do’) to look at the numbers and what they know about them in relation to this.
In child speak, we would expect their internal voice to say, “15 could be split into a 10 and a 5. Multiplying by 10 is easy. Then I just halve my answer to find 5 times, because 5 is half of 10. Then I’ll add those 2 bits together to find 15”.
Situation 2 – Applying in an investigative problem
Tao is thinking of two numbers. When the large number is subtracted from the smaller number, the difference is 5. When they are multiplied together, the answer is 36. What are the 2 numbers?
There are a few methods that could be used to solve this and there’s nothing wrong with trying a few methods to figure out how best to solve it.
However, it is always best that students look at what they know before they do this. Here, students may be mindful by thinking about how the problem involves subtraction (so addition may be useful) and multiplication (so division may be useful).
When that doesn’t help much, they might estimate and pick 2 numbers and see if they fit, “I know that 10 – 5 = 5. I’ll write that down. 5 x 10 doesn’t equal 36 though, so maybe I should look at the multiplication part more and also re-read the question.
If they’re multiplied together then that must mean factors of 36! Got it, I can list the factors of 36 and then see which will subtract to make 5. Okay, 1,2,3,4,6,9,12,18,36… 9 x 4 = 36 and 9 – 4 = 5. It’s 9 and 4!”
See also: Lowest common multiple , Greatest common factor & What is a multiple
This would be one possible example of a child showing mindfulness. It does not mean it is the most or only efficient way, but it demonstrates how using what they already know can support them in directing their pursuit of the answer.
Mental rather than written strategies
Students that use mental strategies when a written would have been more efficient are often harder to ‘crack’ as they will flit from never using written methods to always using it and back again. It is because of their lack of mindfulness that this is occurring.
Tackling problems such as those above with these students in small groups or whole classes and ‘lifting the veil’ on the potential approaches taken will develop the same skills in them.
However, at the end of the day, we want them to eliminate errors that can be made when overusing mental methods. So as a general rule of thumb and sticking plaster for these students while building their mindfulness, stop them when they are mid-calculation and ask them whether they feel outside their ‘comfort zone’.
If they are, ask them if they could note anything down they haven’t yet that could put them back in their comfort zone.
Then ask if they can juggle what is in their head with their notes and if they are still very clear in what they are doing/where they are going. In other words, are they being stretched too far in too many directions?
If your students have gaps that need filled, don’t panic! Get in touch with our school’s team who can arrange a free demo of our one-to-one math interventions.
Do you have students who need extra support in math?
Skye—our AI math tutor built by experienced teachers—provides students with personalized one-on-one, spoken instruction that helps them master concepts, close skill gaps, and gain confidence.
Since 2013, we’ve delivered over 2 million hours of math lessons to more than 170,000 students, guiding them toward higher math achievement.
Discover how our AI math tutoring can boost student success, or see how our math programs can support your school’s goals:
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
The content in this article was originally written by deputy headteacher Pete Richardson and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.