High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Calculator skills Sequences Fractions

Percentages

Math resources Statistics and probability Sampling methods

Systematic samp.

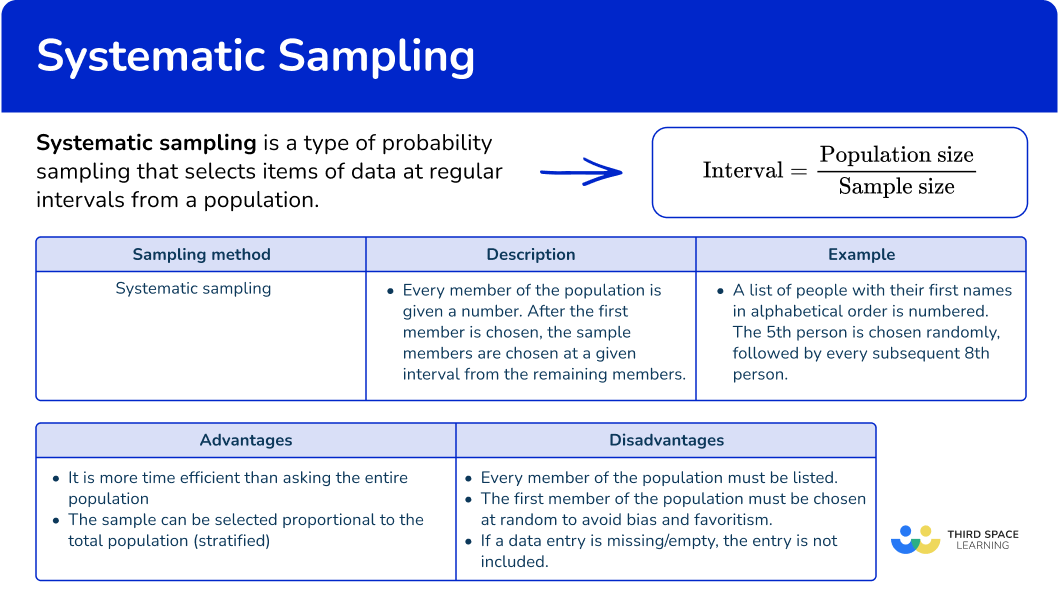
Systematic sampling

Here you will learn about systematic sampling, including what systematic sampling is, how systematic sampling works, and the advantages and disadvantages of systematic sampling.

Students will first learn about systematic sampling as part of statistics and probability in $7$ th grade.

What is systematic sampling?

Systematic sampling is a type of probability sampling that selects items of data at regular intervals from a population.

Every data entry for the population must be given in a list (a sampling frame) so that they have an equal chance (equal probability) of being selected.

You select the first item of data using a random number generator and then select the rest at regular intervals (fixed intervals).

[FREE] Probability Worksheet (Grade 7 to 12)

Teaching systematic sampling? Use this quiz to check your grade 7 to 12 students’ understanding of probability. 15+ questions with answers covering a range of probability topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Probability Worksheet (Grade 7 to 12)

DOWNLOAD FREE

The sampling interval

To calculate the interval required to select the sample data, you calculate the size of the population divided by the size of the sample.

$\text{Sampling interval}=\cfrac{\text{Population size}}{\text{Sample size}}$

For example,

If the population size is $1200$ and the desired sample size is $400$ items of data, you divide $1200$ by $400$ to get an interval of $3.$ This means that every $3$ rd item of data in the ordered list is selected for the sample.

For example,

A factory that manufactures cars must regularly assess the quality of production. In one month, $5 \%$ of cars are selected using a systematic sample to be rigorously tested for quality purposes. The first car is chosen at random then every $10$ th car that follows.

This systematic sample helps the company to ensure the quality of their car manufacture is maintained. Testing each vehicle would be costly and take too much time.

Advantages and disadvantages of systematic sampling

Following a systematic sampling methodology has advantages and disadvantages:

What is systematic sampling?

Common Core State Standards

How does this relate to $7$ th grade math and high school math?

Grade 7 – Statistics and Probability (7.SP.A.1)
Understand that statistics can be used to gain information about a population by examining a sample of the population; generalizations about a population from a sample are valid only if the sample is representative of that population.

Understand that random sampling tends to produce representative samples and support valid inferences.

High School – Statistics and Probability (HS.S.IC.B.3)
Recognize the purposes of and differences among sample surveys, experiments, and observational studies; explain how randomization relates to each.

High School – Statistics and Probability (HS.S.IC.B.4)
Use data from a sample survey to estimate a population mean or proportion; develop a margin of error through the use of simulation models for random sampling.

How to take a systematic sample

In order to take a systematic sample:

Order the population and give each data entry a unique reference number.
Calculate the number of items of data in the sample.
Calculate the interval.
Use a random number generator to select the first item of data.
Select the remaining items of data following the given sequence.

Systematic sampling examples

Example 1: systematic sampling – production line

A company produces biscuits at $100$ per minute. A machine checks the weight of $10 \%$ of the biscuits.

The biscuits pass through the machine one at a time. Use systematic random sampling to select the biscuits for the sample over $3$ minutes.

Order the population and give each data entry a unique reference number.

As each biscuit passes through the machine one at a time, you can assume that the first biscuit is number $1,$ the second is biscuit number $2,$ etc.

2Calculate the number of items of data in the sample.

In $3$ minutes, there will be $3 \times 100=300$ biscuits. As the company checks $10 \%$ of the biscuits, you need a sample of:

$\cfrac{300}{100}\times{10}=30$ biscuits.

3Calculate the interval.

As you need $30$ biscuits, and you are using a systematic sample, you need to choose the biscuits using a sequence. You determine the interval in the sequence by dividing the sample size by the population size:

\text{Interval}=\cfrac{\text{Population size}}{\text{Sample size}}=\cfrac{300}{30}=10

So you need to pick every $10$ th item in the ordered data set.

4Use a random number generator to select the first item of data.

As you need to pick every $10$ th term, the first number in the sample (starting point of the sequence) must be randomly chosen from the first $10$ terms.

Using a random number generator, you get the number $6,$ so you choose the first item of data in the sample to be the $6$ th biscuit.

Below you have used a table to show how the sequence develops*:

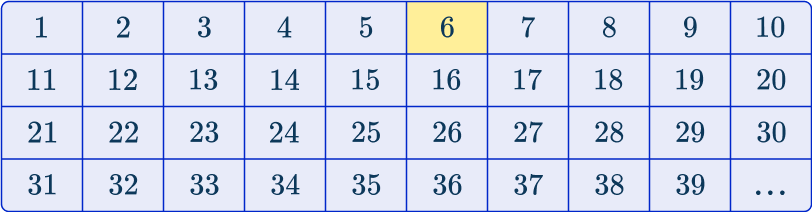
*This table only contains the first $39$ biscuits of the $300$ in the population.

5Select the remaining items of data following the given sequence.

As you are selecting every $10$ th item, you can select the following biscuits from the data:

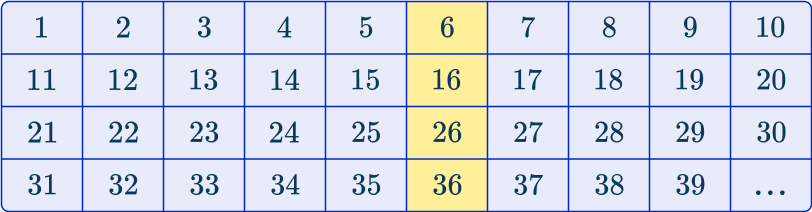
The sample will therefore contain $30$ biscuits with the following numbers:

6, \, 16, \, 26, \, 36, \, 46, \, 56, \, 66, \, 76, \, 86, \, 96, \, 106, \, 116,

126, \, 136, \, 146, \, 156, \, 166, \, 176, \, 186, \, 196, \, 206,

$216, \, 226, \, 236, \, 246, \, 256, \, 266, \, 276, \, 286,$ and $296.$

Note: These numbers are in the sequence $10n-4.$

Example 2: systematic sampling – sample as percentage of population

Luke is looking at the beats per minute of tracks in his music player. He has $1,200$ tracks. He decides to take a systematic sample of $25 \%$ of his tracks. Determine the tracks that should be chosen.

Order the population and give each data entry a unique reference number.

Show step

Use the number of plays to sort the data into an order. The first track in the list will be number $1,$ the second track number $2,$ etc.

Calculate the number of items of data in the sample.

Show step

As Luke wants a sample of $25 \%,$ you need to calculate $25 \%$ of $1,200\text{:}$

$\cfrac{1200}{100}\times{25}=300$ tracks.

Calculate the interval.

Show step

As you need $300$ tracks, and you are using a systematic sample, you need to choose the tracks using a sequence. The interval is:

$\text{Interval}=\cfrac{\text{Population size}}{\text{Sample size}}=\cfrac{1200}{300}=4$

So you need to pick every $4$ th term in the data.

Use a random number generator to select the first item of data.

Show step

As you need to pick every $4$ th term, the first number in the sample must be randomly chosen from the first $4$ terms.

Using a random number generator, you get the number $1,$ so you choose the first item of data in the sample to be the $1$ st track.

Below you have used a table to show how the sequence develops*:

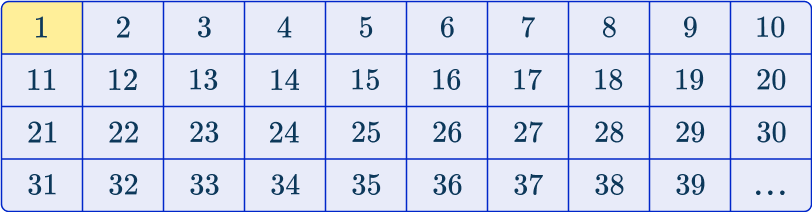
*This table only contains the first $39$ tracks of the $1,200$ in the population.

Select the remaining items of data following the given sequence.

Show step

As you are selecting every $4$ th item, you can select the following tracks from the data:

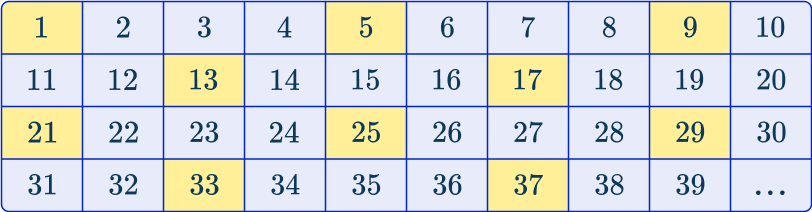
The sample will therefore contain $300$ tracks that belong to the sequence $4n-3.$

Example 3: systematic sampling – small sample size

A traffic management company is researching the proportion of lorries that use a single carriageway between $8\text{:}00$ am and $9\text{:}00$ am. A traffic camera records the details of every vehicle and produces a list of data in the order of the time that the vehicle passes the camera.

$960$ vehicles are recorded within the hour on one day. The company uses a systematic sample to select a random sample of $5 \%$ of the data for their research. Determine which vehicles will be in the sample.

Order the population and give each data entry a unique reference number.

Show step

The population data is in order given their time stamp and so you can list the first vehicle in the list as number $1,$ second vehicle is number $2,$ etc.

Calculate the number of items of data in the sample.

Show step

The sample size is $5 \%$ so you need to calculate $5 \%$ of $960\text{:}$

$\cfrac{960}{100}\times{5}=48$ vehicles.

Calculate the interval.

Show step

As you need $48$ vehicles, the interval is:

$\text{Interval}=\cfrac{\text{Population size}}{\text{Sample size}}=\cfrac{960}{48}=20$

So you need to pick every $20$ th item of data.

Use a random number generator to select the first item of data.

Show step

As you need to pick every $20$ th term, the first number in the sample must be randomly chosen from the first $20$ terms.

Using a random number generator, you get the number $17,$ so you choose the first item of data in the sample to be the $17$ th vehicle.

Below you have used a table to show how the sequence develops*:

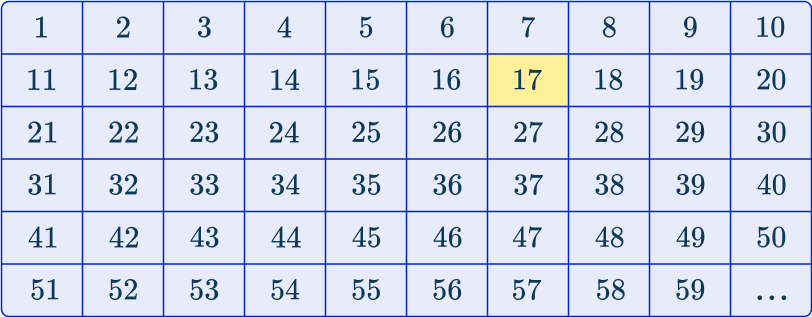
*This table only contains the first $59$ vehicles of the $960$ in the population.

Select the remaining items of data following the given sequence.

Show step

As you are selecting every $20$ th item, you can select the following vehicles from the data:

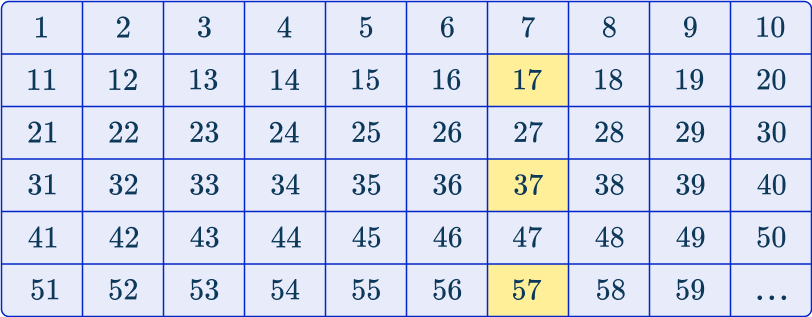
The sample will therefore contain $48$ vehicles that belong to the sequence $20n-3.$

Example 4: systematic sampling – large population

A local council is researching the distribution of voters in $15,000$ homes. They take a systematic sample of $20 \%$ of homes, listed in order of their zip code and house number. Determine which homes will be asked to participate in the survey.

Order the population and give each data entry a unique reference number.

Show step

The population data is in order given their zip code and house number and so you can assume that the first home on the list is number $1,$ the second home number $2,$ etc.

Calculate the number of items of data in the sample.

Show step

The sample size is $20 \%$ so you need to calculate $20 \%$ of $15,000\text{:}$

$\cfrac{15000}{100}\times{20}=300$ homes.

Calculate the interval.

Show step

As you need $300$ homes, and you are using a systematic sample, you need to choose the homes using a sequence. The interval for this set of data is equal to:

$\text{Interval}=\cfrac{\text{Population size}}{\text{Sample size}}=\cfrac{15000}{300}=50$

So you need to pick every $50$ th term in the data.

Use a random number generator to select the first item of data.

Show step

As you need to pick every $50$ th term, the first number in the sample must be randomly chosen from the first $50$ terms.

Using a random number generator, you get the number $8,$ so you choose the first item of data in the sample to be the $8$ th home.

Below you have used a table to show how the sequence develops*:

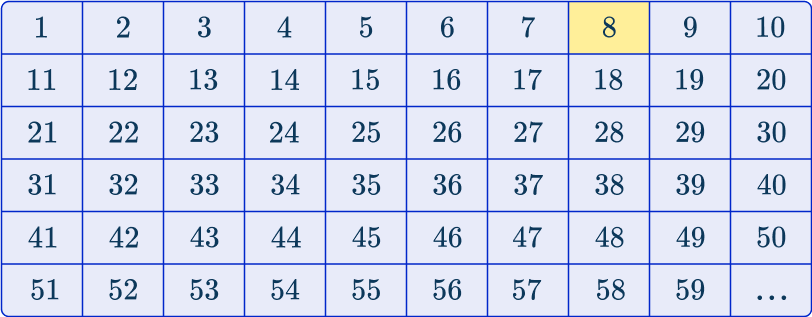
*This table only contains the first $59$ homes of the $15,000$ in the population.

Select the remaining items of data following the given sequence.

Show step

As you are selecting every $50$ th item, you can select the following homes from the data:

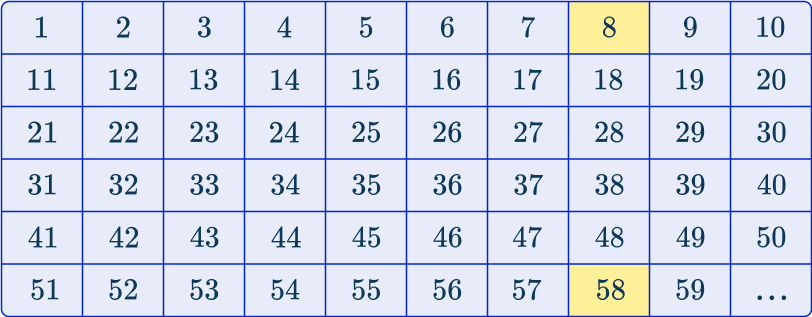
The sample will therefore contain $300$ homes that belong to the sequence $50n-42.$

Example 5: systematic sampling – small sample

An online clothing company is researching the average customer spend over the previous month. There were $12,664$ orders purchased, and each order has a unique reference number.

The company takes a systematic sample of $2 \%$ of orders. Determine which orders will be chosen for the sample.

Order the population and give each data entry a unique reference number.

Show step

As each order has a unique reference number, you can order the numbers from smallest to largest, and then number each item of data from $1-12,664.$

Calculate the number of items of data in the sample.

Show step

As the company is taking a sample of $2 \%,$ you need to calculate $2 \%$ of $12,664\text{:}$

$(12664 \div 100) \times 2=253.28$

The sample size is $253$ orders.

Calculate the interval.

Show step

The interval is equal to

$\text{Interval}=\cfrac{\text{Population size}}{\text{Sample size}}=\cfrac{12664}{253}=50\text{ (nearest whole number)}$

Use a random number generator to select the first item of data.

Show step

Using a random number generator, you need to select the first item of data from the first $50$ orders. The random number chosen is $13.$

The first item of data in the list is the $13$ th order.

Select the remaining items of data following the given sequence.

Show step

As the interval is $50,$ the next order will be $13+50=63,$ then $63+50=113,$ then $113+50=163 …$ and so on until you have selected the $253$ items of data.

The sample will therefore contain $253$ items of data that belong to the sequence $50n-37.$

Example 6: systematic sampling – deciding the population size

A café is carrying out some market research. Out of $1240$ customers that entered the café during a weekend, $950$ allowed the café to email them a questionnaire.

The café takes a systematic sample size of $12 \%$ of those who received the questionnaire. Determine which customers will be part of the sample.

Order the population and give each data entry a unique reference number.

Show step

Despite there being $1240$ customers, the population size is $950$ as these customers received a questionnaire.

As they provided an email address, the population can be listed using their email address, in alphabetical order.

Calculate the number of items of data in the sample.

Show step

The café is taking a sample size of $12 \%.$

$(950 \div 100) \times 12=114$

The sample will contain $114$ items of data.

Calculate the interval.

Show step

The interval is

$\text{Interval}=\cfrac{\text{Population size}}{\text{Sample size}}=\cfrac{950}{114}=8\text{ (nearest whole number)}$

Use a random number generator to select the first item of data.

Show step

As every $8$ th customer is being selected, the first customer must be randomly chosen from the first $8$ items of data. Using a random number generator, the $4$ th customer is chosen.

Select the remaining items of data following the given sequence.

Show step

As the first customer is number $4,$ and every $8$ th customer is being selected after, you continue to add $8$ to the previous value in the sequence until you have selected the $114$ customers (items of data).

This follows the sequence $8n-4.$

Teaching tips for systematic sampling

Make sure students understand the systematic sampling definition and how it differs from other methods of sampling like simple random sampling and stratified sampling. This understanding will help them grasp when and why each method is used in research and data collection.

Provide worked examples showing different scenarios, such as different population sizes and sampling intervals.

Discuss real-world applications where systematic sampling is used, such as in market research or quality control in manufacturing.

Teach students strategies to minimize sampling errors, such as ensuring a random starting point, verifying the completeness of the population list, and considering alternative sampling methods when systematic biases are suspected.

Easy mistakes to make

Mixing up a sampling method
Using the incorrect sampling process to select data (such as using systematic sampling or non-random sampling).

Ignoring random start
Forgetting to randomly select the starting point can introduce bias if there’s any hidden pattern in the list.

Data not in order
When you are finding the median value in a set of data, the data must be in order, otherwise the number being picked is not the median, it’s just the middle number in a random list. This is the same for a systematic sample.

Every item of data is structured in an order from a sampling frame (age, zip code, alphabetical order etc), and then your sample is taken.

Incorrectly calculating the interval for the sample
Let’s assume you have $1,000$ items of data. $5 \%$ of $1,000$ is $50$ so you need $50$ items of data.

Those $50$ items of data must be spread equally across all of the ordered data, so by dividing the number in the population by the sample size, you find the interval between each item of data.

Here you would have $\cfrac{1000}{50}=20.$ You would choose every $20$ th item in the list of $1,000$ items to get a sample of $50.$

Practice systematic sampling questions

Order and number the items in the list. Find $20 \%$ of the total population. Calculate the interval. Select the first number using a random number generator. Select every $5$ th item in the list afterward.

Split the total population into smaller categories. Calculate $20 \%$ of each category. Use a random number generator to select items in each category, proportional to the total.

Order the population and assign each item of data a unique number. Use a random number generator to select every $20$ th item in the list.

Select the first $20 \%$ of items of data in the list.

For a sample of $20 \%,$ you need to calculate $20 \%$ of the population. Here, $20 \%$ of $1350$ is $270,$ so you need $270$ listed items.

As the sampling technique is systematic, you need to calculate the interval (the sequence) for which the items in the list will be selected.

Here, as you want $20 \%$ of the population, this is equivalent to every fifth item of data in the list $(20 \%=\cfrac{20}{100}=\cfrac{1}{5}).$

To determine which item in the list is first, you need to use a random number generator to select one of the first five items in the list only. Here, a random number generator selected the first item in the list to be the $3$ rd item listed.

So, by starting at the randomly selected $3$ rd item in the ordered population list, and selecting every $5$ th item in the population as you want a sample size of $20 \% \; (270$ items $),$ you generate a systematic sample.

$12, \, 21,$ and $30$

$4, \ 8, \, 12, \, 16, \, 20, \, 24, \, 28,$ and $32$

$7, \, 11, \, 15, \, 19, \, 23, \, 27, \, 31$ and $35$

$4, \, 5, \, 6, \, 7, \, 8, \, 9, \, 10,$ and $11$

$25 \%$ of $36=9$ so the sample size contains $9$ members of staff.

$\cfrac{9}{36}=\cfrac{1}{4}$ so every $4$ th person is chosen after person $3.$

20

9

18

6

$5 \%$ of $120=6$ items of data

$\cfrac{120}{6}=20$ so every $20$ th item of data is chosen

$118\div{20}=5.9$ so you can subtract $20$ from $118$ five times, leaving us with the number $18$ as the first in the list.

Tuesday

Saturday

Thursday

Monday

Half of the data means every other day, which gives us every odd number in the month. The last odd number in the month is $29,$ which is a Monday.

3n

n+6

6n-3

6n

The first number in the sequence is $3.$

The number of students in the sample is $16 \%$ of $2,243,$ which is equal to:

(2243\div{100})\times{16}=359\text{ (nearest whole)}

The interval is equal to

\text{Interval}=\cfrac{\text{Population size}}{\text{Sample size}}=\cfrac{2243}{359}=6\text{ (nearest whole number)}

The first $5$ terms in the sequence are therefore: $3, \, 9, \, 15, \, 21, \, 27, \, …$

The common difference in the sequence is $+6,$ so you have the sequence $6n.$

The first term in the sequence $6n$ is $6\times{1}=6.$ You need the first term to equal $3,$ so you have to subtract $3$ from $6n,$ giving us the nth term $6n-3.$

6. A hotel has $18$ floors. Each floor has $4$ apartments, except for the ground floor which has $2$ apartments, and the top floor which is one single apartment.

Each apartment is given a unique reference number according to the floor level and the apartment number (for example, apartment $2$ on floor $16$ is number $162$ ).

A hotel inspector is required to inspect $4 \%$ of apartments, chosen using a systematic sample. The first apartment that is inspected is randomly selected to be number $012.$

This is the $4$ th apartment in the list. What is the number of the last apartment to be inspected?

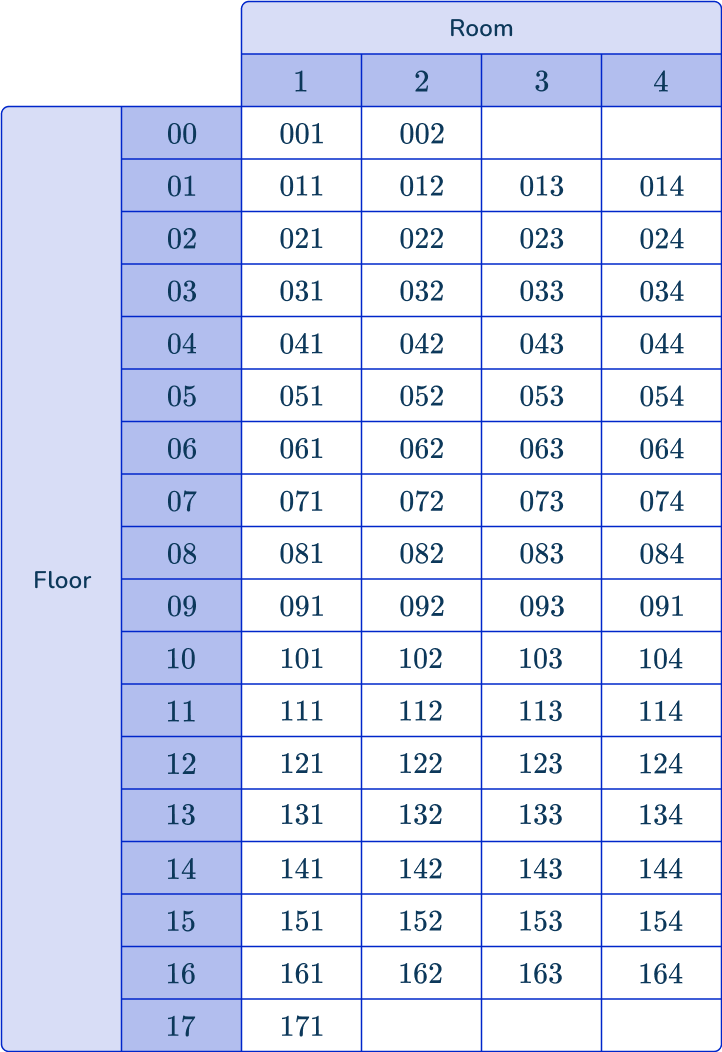
Systematic Sampling image 12 US

122

053

162

134

There are $16$ floors with $4$ apartments $(116\times{4}=64).$

There is $1$ floor with $2$ apartments $(1\times{2}=2).$

There is $1$ floor with $1$ apartment $(1).$ Adding these together, you have the total number of apartments to be $64+2+1=67.$

You need a sample of $4 \%$ of $67\text{:}$

$(67\div{100})\times{4}=3$ (to the nearest whole number) rooms.

The interval is equal to

\text{Interval}=\cfrac{\text{Population size}}{\text{Sample size}}=\cfrac{67}{3}=22\text{ (to the nearest whole number)}

The positions of the $3$ rooms in the list are:

$012$ – the $4$ th apartment in the list (this was given)

$4+22=26$ th apartment in the list (number $064$ )

$26+22=48$ th apartment in the list (number $162$ )

The last room that will be inspected is apartment $2$ on floor $16.$

Systematic sampling FAQs

What is systematic sampling?

Systematic sampling is a probability sampling method where every nth element from a complete list is selected after a random starting point. This method is efficient and straightforward, often considered to have a low risk of data manipulation by statisticians.

What are the different types of systematic sampling?

The different types of systematic sampling are linear systematic sampling, circular systematic sampling, and stratified systematic sampling.

How does systematic sampling differ from simple random sampling?

Systematic sampling selects every nth item after a random start, while simple random sampling selects items entirely by chance. Systematic sampling is generally more efficient and easier to implement than simple random sampling.

How do you know when to use systematic sampling?

Use systematic sampling when the target population is homogeneous and elements are evenly distributed, you have a complete and accurate list of the population, and there are no periodic patterns in the population list that could bias the sample.

For instance, systematic sampling is suitable for selecting every $10$ th patient from a hospital database for a satisfaction survey.

How does systematic sampling differ from cluster sampling?

Systematic sampling selects every nth item from a complete list after a random start, ensuring uniform coverage.

Cluster sampling divides the population into clusters, randomly selects some clusters, and then includes all elements or a random sample from the chosen clusters, making it useful for geographically dispersed populations.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.