Percent of a Number - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Simplifying fractions Percent to decimal Percent to fraction

Math resources Ratio and proportion Percent

Percent of a number

Here is everything you need to know about finding the percent of a number, including how to solve with or without a calculator.

Students will first learn about finding the percent of a number as part of ratios and proportions in 6th grade.

What is a percent of a number?

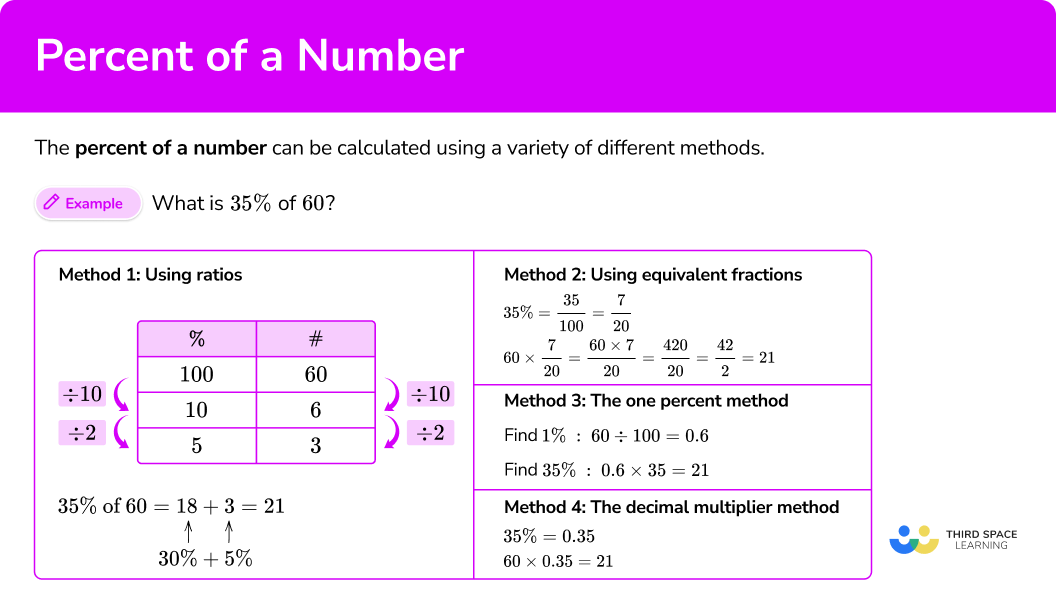
The percent of a number can be calculated using a variety of different methods.

For example, what is $35\%$ of $60?$

Method 1: Using ratios

Start with $60,$ which is the whole, or $100\%,$ and work down the table using ratios.

Now use the ratios in the table to find $35\%.$

$10 \% \times 3=30\%$ and $6 \times 3=18,$ so $30\%$ is $18$ and the table shows that $5\%$ is $3.$

\begin{aligned} 35\% \text{ of } 60 &= 18 \, + \, 3=21 \\ & \quad \; ↑ \quad \;\; ↑ \\ & \;\; 30\% \, + \, 5\% \end{aligned}

Method 2: Using equivalent fractions

Write the percent as a fraction in its lowest terms and then multiply the number by this fraction.

35\% = \cfrac{35}{100} =\cfrac{7}{20}

60 \times \cfrac{7}{20} = \cfrac{60\times 7}{20} = \cfrac{420}{20} =\cfrac{42}{2}= 21

Method 3: The one percent method

Find $1\%$ first by dividing the amount by $100$ and then multiply the percent (as a whole number).

60 \div 100 \times 35=21

Note, this works because $60 \div 100 \times 35=60 \times \cfrac{35}{100}.$

Method 4: The decimal multiplier method

First, convert the percent into a decimal, and then multiply the amount by this decimal.

35\%=0.35

60 \times 0.35=21

Methods $1$ and $2$ lend themselves to questions where a calculator is not allowed.

Methods $3$ and $4$ lend themselves to questions where calculators are allowed.

What is a percent of a number?

[FREE] Percents Worksheet (Grade 6 to 7)

Use this quiz to check your grade 6 to 7 students’ understanding of percents. 10+ questions with answers covering a range of 6th and 7th grade percent topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Percents Worksheet (Grade 6 to 7)

DOWNLOAD FREE

Common Core State Standards

How does this relate to 6th grade math?

Grade 6 – Ratios and Proportional Relationships (6.RP.A.3c)
Find a percent of a quantity as a rate per $100$ (for example, $30\%$ of a quantity means $\frac{30}{100}$ times the quantity); solve problems involving finding the whole, given a part and the percent.

How to find the percent of a number

In order to find the percent of a number with or without a calculator:

Identify the percent and consider if there is a simple equivalent fraction.
Decide which method to use.
Work out the answer.

Percent of a number examples

Example 1: simple percent without a calculator

Find $75\%$ of $120 \ km.$

Identify the percent and consider if there is a simple equivalent fraction.

75 \%=\cfrac{75}{100}=\cfrac{3}{4}

2Decide which method to use.

You can use $75\%$ as a fraction to solve or, since $75\%$ is easily related to $25\%$ and $50\%$ , you can use ratios to solve.

3Work out the answer.

Start with $120,$ which is the whole, or $100\%,$ and work down the table using ratios.

Now use the ratios in the table to find $75\%.$

$75\% = 50\% + 25\%,$ so $75\% = 60 + 30.$

$75\%$ of $120$ is $90.$

Example 2: simple percent without a calculator

Find $10\%$ of $450 \ kg.$

Identify the percent and consider if there is a simple equivalent fraction.

10\%=\cfrac{10}{100}=\cfrac{1}{10}

Decide which method to use.

To find $10\%$ , you can solve $450 \times \cfrac{1}{10} \,$ (which is equal to $450 \div 10$ ).

Work out the answer.

450 \times \cfrac{1}{10}=\cfrac{450}{10}=45

$450\div 10 = 45$

$10\%$ of $450 \ kg$ is $45 \ kg.$

Example 3: percent decomposed to 10% and 1%

Find $16\%$ of $\$300.$

Identify the percent and consider if there is a simple equivalent fraction.

16 \%=\cfrac{16}{100}=\cfrac{8}{50}=\cfrac{4}{25}

Decide which method to use.

You could use a fraction method with any of the equivalent fractions, but since the numbers in the numerator and denominator are not small numbers, there are simpler ways to solve.

In this case, you can break $16\%$ down into groups of $10\%$ and $1\%.$

Work out the answer.

16\%= 10\% + 6\times 1\%

To find $10\%$ . you can divide by $10$ :

$300\div 10 = 30$

To find $1\%$ , you can divide by $100$ :

$300\div 100 = 3$

So, $16\%$ of $300$ is:

$\begin{aligned} & \; 30 + (6 \times 3) = 30 + 18 = 48\\ & \;\; ↑ \quad \quad ↑ \\ &10 \%+1 \% \times 6 \end{aligned}$

$16\%$ of $\$300$ is $\$48.$

Example 4: the 1% method

Find $23\%$ of $700.$

Identify the percent and consider if there is a simple equivalent fraction.

23\% = \cfrac{23}{100}

Decide which method to use.

$\cfrac{23}{100} \,$ is in lowest terms, so this relationship can’t be shown with smaller numerators or denominators.

It will be quicker to use a method that doesn’t involve fractions. In this case, you can find $1\%$ of $700$ and use that to find $23\%.$

Work out the answer.

To find $1\%,$ you can divide by $100$ :

$700\div 100 = 7$

So, $23\%$ of $700$ is:

$\begin{aligned} &7 \times 23=161 \\ &↑ \\ &1\% \end{aligned}$

$23\%$ of $700$ is $161.$

Example 5: decimal multiplier

Work out $78\%$ of $\$411.$

Identify the percent and consider if there is a simple equivalent fraction.

78 \%=\cfrac{78}{100}=\cfrac{39}{50}

Decide which method to use.

You could use a fraction method with any of the equivalent fractions, but since the numbers in the numerator and denominator are not small numbers, there are simpler ways to solve.

In this case, you can convert $78\%$ to a decimal and multiply by the number to solve.

Work out the answer.

78\%=\cfrac{78}{100}=0.78

$411 \times 0.78=320.58$

$78\%$ of $\$411$ is $\$320.58.$

Example 6: decimal multiplier

Work out $61\%$ of $728.$

Identify the percent and consider if there is a simple equivalent fraction.

61 \%=\cfrac{61}{100}

Decide which method to use.

$\cfrac{61}{100}$ is in lowest terms, so this relationship can’t be shown with smaller numerators or denominators. It will be quicker to use a method that doesn’t involve fractions.

In this case, you can convert $61\%$ to a decimal and multiply by the number to solve.

Work out the answer.

61\%=\cfrac{61}{100}=0.61

$728 \times 0.61=444.08$

$61\%$ of $\$728$ is $\$444.08.$

Teaching tips for percent of a number

Worksheets have their place for learning how to find the percent of a number, but they also ensure that students have plenty of opportunities to share their thinking with others. As this page outlines, there are many different ways to go about solving percentage problems, which means there are many opportunities for students to talk and think critically about their work and the work of others.

There are many different real world situations that students can connect to when learning this topic, such as finding the sales tax on an original price or calculating the sale price based on a percentage decrease.

Give students time to specifically look for patterns with a calculator as they find different percents of the same number. Ask questions like, “How do you notice the decimal places changing?” or “What do you notice about the percent of a number and the original number?” to encourage student thinking.

Once students have a foundational understanding of this topic and can flexibly move between strategies, it is okay to let them use a percentage calculator or other online calculators that do the calculations for them. This allows students to shift their focus to more complicated word problems or real-world application for percent of a number.

Easy mistakes to make

Incorrectly converting from a percent to a decimal
When a percent is represented with a percent symbol, to convert it to a decimal you must divide by $100$ (which is the same as moving the decimal point two places to the left) before multiplying.
For example,
What is $53\%$ of $200?$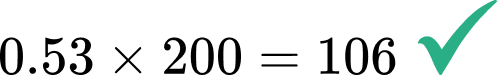

Adding or subtracting the same thing in a ratio table
A ratio table can be used to represent the multiplicative relationship between a number and a percent of that number. Adding or subtracting the same thing from both sides does not preserve that relationship.
For example,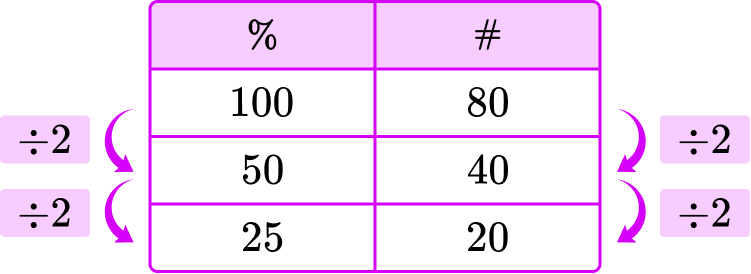

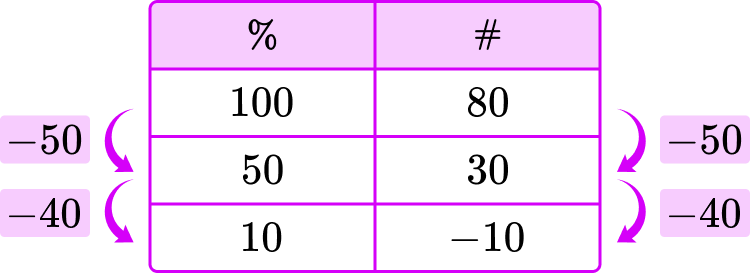
Making calculation mistakes when multiplying by a fraction or dividing by a whole number
It is a good idea to always check your work after solving (with or without a calculator). A good way to do this is to consider what a reasonable answer should be.
For example,
What is $11\%$ of $220?$
Before solving, notice that $11\%$ is close to $10\%$ and $10\%$ of a number is like dividing by $10$ or moving the decimal to the left once, so the answer should be close to $22.$ If you get an answer that is much smaller or larger than $22,$ it most likely means you made a mistake calculating and you should check your work.

Not filling both decimal positions for a money answer
For example, an answer of $\$16.5$ should be written as $\$16.50.$ There are two digits needed to include the penny position.

Percent of a number practice questions

\$140

\$28

\$240

\$70

$25\%$ is easily related to $100\%$ and $50\%,$ so you can use ratios to solve.

Start with $280,$ which is the whole, or $100\%,$ and work down the table using ratios.

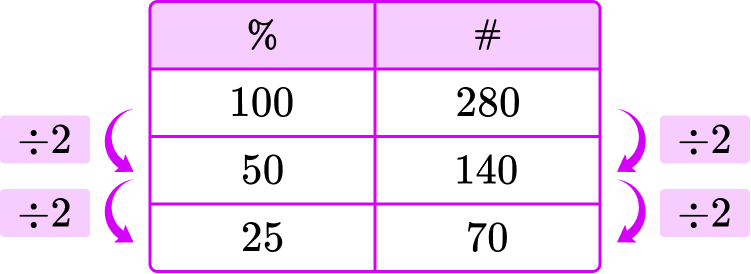
Percent of a Number practice question 1

$25\%$ of $\$280$ is $\$70.$

35 \, kg

7 \, kg

17.5 \, kg

50 \, kg

50 \%=\cfrac{50}{100}=\cfrac{25}{50}=\cfrac{5}{10}=\cfrac{1}{2}

$\cfrac{1}{2} \,$ is the simplest fraction for $50\%,$ so it will be the easiest to solve with.

So you can calculate…

\$ 70 \times \cfrac{1}{2}=\cfrac{\$ 70}{2}=\$ 35

\$ 70 \div 2=\$ 35

40 \, g

24 \, g

16.67 \, g

25 \, g

$10\%$ of $200$ :

200 \div 10 = 20

$1\%$ of $200$ :

200 \div 100 = 2

\begin{aligned} 12\%&=10\%+(2 \times 1\%)\\\\ &=20+(2 \times 2)\\\\ &=24 \end{aligned}

75 \, km

81 \, km

67 \, km

27 \, km

$10\%$ of $300 \, km$ :

300 \div 10 = 30

$1\%$ of $300 \, km$ :

300 \div 100 = 3

\begin{aligned} 27\%&=(2 \times 10\%) + (7 \times 1\%)\\\\ &=(2 \times 30) + (7 \times 3)\\\\ &=60+21\\\\ &=81 \, km \end{aligned}

\$404.70

\$404.07

\$12.46

\$570

Convert the percent to a decimal, then multiply.

57\%=\cfrac{57}{100} = 0.57

\$710 \times 0.57 = \$404.70

\$30.43

\$83.79

\$148.57

\$143.20

Convert the percent to a decimal, then multiply.

83\%=\cfrac{83}{100}=0.83

\$179 \times 0.83 = \$148.57

Percent of a number FAQs

How do you write a percent in decimal form and fraction form?

A percent is a ratio out of $100,$ so the denominator of the fraction is always $100$ , and the numerator is the percent written as a whole number. To convert this to a decimal, write the percent as a decimal ending in the hundredths column. Note this is true for whole number percents only.

Why is a percent always out of $\bf{100}$ ?

In our number system, percents are a special type of ratio and we use $100$ to represent the whole. The word percent broken up is per-cent, per representing a ratio and ‘cent’ meaning $100,$ like in the word century or $100$ cents in a dollar.

The next lessons are

Compound measures
Converting fractions, decimals, and percentages
Exponents
Algebraic expressions
Ratio

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.