High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Addition and subtraction
Here you will learn strategies on how to add and subtract, including using visual models, the number line, and algorithms.
Students will first learn about addition and subtraction in kindergarten, continue to add and subtract larger numbers in 2 nd and 3 rd grade, and learn the standard algorithm in 4 th grade. In 7 th grade, students learn to add and subtract with integers and then rational numbers.
What are addition and subtraction?
Addition is the operation of combining two or more numbers together. Subtraction is the operation of taking away from a number.
Students as early as pre-k have a basic, informal understanding of addition and subtraction. By the end of Kindergarten, students can operate within 10, heavily relying on models like counters or 10 frames to solve.
By the end of first grade, students should be able to add and subtract fluently within 20. As students work on repeatedly adding and subtracting with single digit numbers, they deepen their number sense around the operations by solving in different ways.
This includes beginning to build number bonds.
For example,
- Seeing 5+4 and knowing the sum is 9 without having to solve.
- Seeing 9-4 and knowing the difference is 5 without having to solve.
This aids students as they go into 2 nd and 3 rd grade and learn to add and subtract multi-digit numbers (within 1,000 ). At this level, students are still relying on number relationships, properties of operations, place value ideas, models, etc. to solve.
For example,
When adding 3- digit numbers, students may combine each place value of the addends separately.
235 + 149
Hundreds \hspace{1.1cm} Tens \hspace{1.2cm} Ones
200 + 100 \hspace{1cm} 30 + 40 \hspace{1cm} 5 + 9 \hspace{1cm}
= 300 \hspace{1.5cm} = 70 \hspace{1.3cm} = 14
And then add in the partial sums:
300+70+14=384
For example,
When subtracting numbers that are larger, students may use what they know about place value to solve.
781-395
The distance from 781-395 is the same as 786-400, it is just shifted up 5 on the number line.
Now solve 786-400 by taking away 4 hundreds.
786-400=386, so 781-395=386.
Once students have developed a flexible understanding of multi-digit addition and multi-digit subtraction in 2 nd grade and 3 rd grade, they learn the standard algorithm in 4 th grade.
For example,
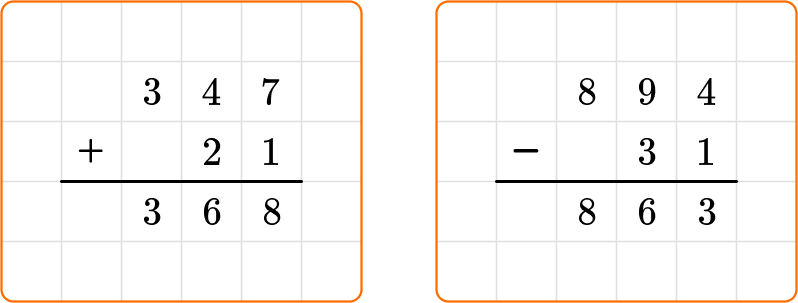
It is important to consider the place value of each digit and line up the corresponding digits in each number.
In 5 th grade and 6 th grade, students continue to add and subtract with whole numbers and apply these strategies to decimal operations.
See also: Adding and subtracting decimals
In 7 th grade, students learn to add and subtract integers and rational numbers.
You can add and subtract integers using visual models or a number line.
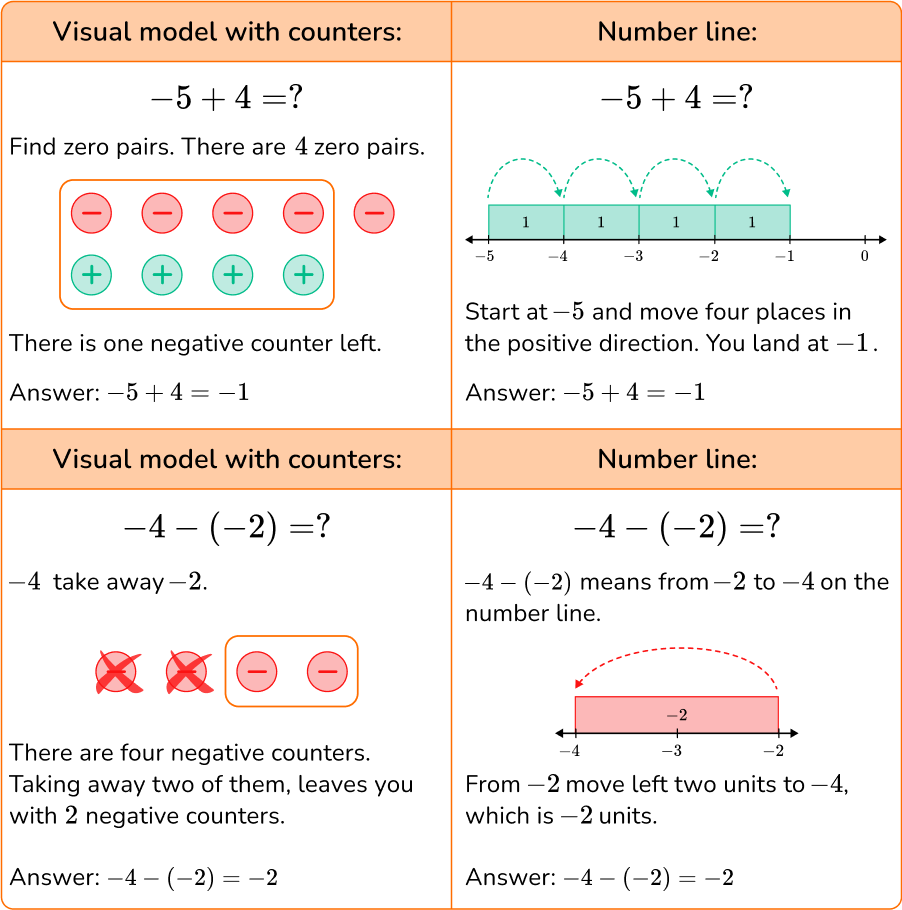
Step-by-step guide: Adding and subtracting integers
You can also add and subtract rational numbers using visual models or a number line.
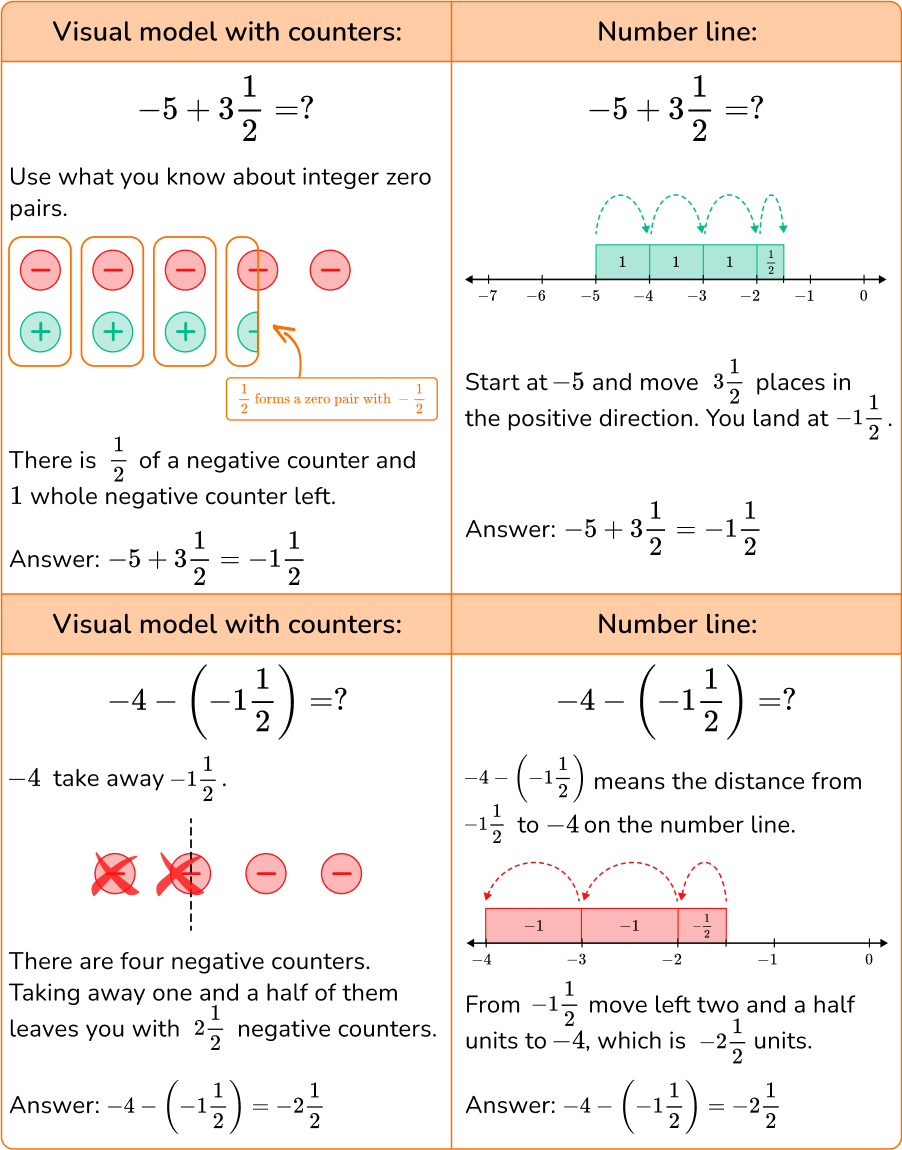
What are addition and subtraction?

![[FREE] Addition and Subtraction Worksheet (Grade 2 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Addition-and-Subtraction-listing-image.png)
[FREE] Addition and Subtraction Worksheet (Grade 2 to 7)
![[FREE] Addition and Subtraction Worksheet (Grade 2 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Addition-and-Subtraction-listing-image.png)
Use this quiz to check your grade 2, 3, 4 and 7 students’ understanding of addition and subtraction. 15+ questions with answers covering a range of 2nd, 3rd, 4th and 7th grade addition and subtraction topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Addition and Subtraction Worksheet (Grade 2 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Addition-and-Subtraction-listing-image.png)
[FREE] Addition and Subtraction Worksheet (Grade 2 to 7)
![[FREE] Addition and Subtraction Worksheet (Grade 2 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Addition-and-Subtraction-listing-image.png)
Use this quiz to check your grade 2, 3, 4 and 7 students’ understanding of addition and subtraction. 15+ questions with answers covering a range of 2nd, 3rd, 4th and 7th grade addition and subtraction topics to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this apply to 2 nd grade math, 3 rd grade math, 4 th grade, and 7 th grade math?
- Kindergarten – Operations and Algebraic Thinking (K.OA.A.2)
Solve addition and subtraction word problems, and add and subtract within 10, e.g., by using objects or drawings to represent the problem.
- Grade 1 – Operations and Algebraic Thinking (1.OA.C.6)
Add and subtract within 20, demonstrating fluency for addition and subtraction within 10. Use strategies such as counting on; making ten (e.g., 8+6=8+2+4=10+4=14 ); decomposing a number leading to a ten (e.g., 13-4=13-3-1=10-1=9 ); using the relationship between addition and subtraction (e.g., knowing that 8+4=12, one knows 12-8=4 ); and creating equivalent but easier or known sums (e.g., adding 6+7 by creating the known equivalent 6+6+1=12+1=13 ).
- Grade 2 – Operations and Algebraic Thinking (2.OA.A.1)
Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
- Grade 2 – Numbers and Operations in Base Ten (2.NBT.B.5)
Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.
- Grade 3 – Numbers and Operations in Base Ten (3.NBT.A.2)
Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
- Grade 4 – Numbers and Operations in Base Ten (4.NBT.A.4)
Fluently add and subtract multi-digit whole numbers using the standard algorithm.
- Grade 7- The Number System (7.NS.A.1)
Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram.
- Grade 7- The Number System (7.NS.A.3)
Solve real-world and mathematical problems involving the four operations with rational numbers.
How to add and subtract
There are a lot of ways to add and subtract. For more specific step-by-step guides, check out the individual pages linked in the “What are addition and subtraction?” section above or read through the examples below.
Addition and subtraction examples
Example 1: two digit addition
Solve 34 + 58.
- Choose a strategy.
You can use a model of the tens and ones.

2Solve.
Combine the tens and ones.

You can create one new group of ten from 10 ones.
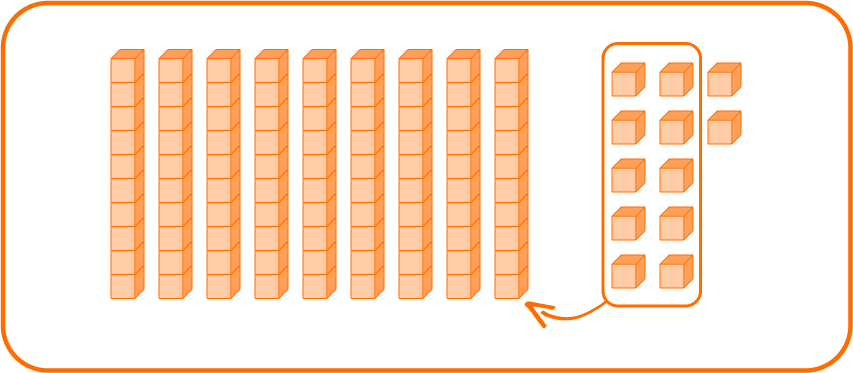
This leaves 9 tens and 2 ones, which is 92.

So, 34+58=92.
Example 2: three digit subtraction
Solve 340-291.
Choose a strategy.
You can use a number line to count up to 340 from 291.

Solve.

The difference between 291 and 340 is 49.
So, 340-291=49.
Example 3: addition with the algorithm
Add 4,297 + 381 with the algorithm.
Stack the numbers and line up the place values.

Add each column from right to left and regroup the numbers when necessary.

Write your final answer and check to make sure your answer is reasonable.
You can estimate to decide if your answer is reasonable.
4,297 rounds to 4,300.
381 rounds to 400.
4,300+400=4,700, so the answer should be close to 4,700. Since 4,678 is close, the answer is reasonable.
4,297+381=4,678
Example 4: subtraction word problem with the algorithm
After the harvest, a farmer has 2,148 pears. 213 of the pears are rotten and cannot be sold. If the farmer sells the rest, how many pears will she sell?
Write an equation that represents the word problem.
2,148 - 213 = ⬜
Stack the numbers and line up the place values.

Subtract each column from right to left and exchange for a \bf{10} when necessary.
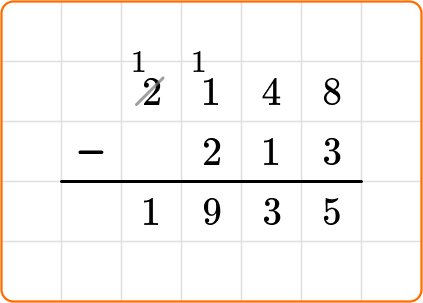
Write your final answer and check to make sure your answer is reasonable.
You can estimate to decide if your answer is reasonable.
2,148 rounds to 2,000.
213 rounds to 200.
2,000-200=1,800, so the answer should be close to 1,800. Since 1,935 is close, the answer is reasonable.
2,148-213=1,935
Example 5: subtracting integers with models
Subtract: -4 -(-6)=?
Represent the problem with counters, identifying zero pairs with addition or adding zero pairs when necessary for subtraction.
-4 - (-6) starts with -4 and removes -6. Add 2 zero pairs in order to remove -6.

The answer is the leftover counters.
There are two positive counters left.
-4-(-6)=2
Example 6: adding rational numbers with the algorithm
Solve -34 \cfrac{2}{3}+\left(-567 \cfrac{3}{4}\right) .
Make sense of the calculation – relating to positive numbers when necessary.
-34 \cfrac{2}{3}+\left(-567 \cfrac{3}{4}\right) combines two negative amounts, which do not create zero pairs.
This means the answer will be even more negative. You can use the algorithm for addition to see what the total amount is.
Use an algorithm.
\begin{aligned}& 34 \frac{2}{3}+567 \frac{3}{4} \\\\ & =34 \frac{2 \times 4}{3 \times 4}+567 \frac{3 \times 3}{4 \times 3} \\\\ & =34 \frac{8}{12}+567 \frac{9}{12} \\\\ & =601 \frac{17}{12} \text { or } 602 \frac{5}{12}\end{aligned}
Decide if the final answer is positive or negative.
Adding two negative numbers results in a negative number. For example, if you started on the number line and went back 34 \cfrac{2}{3} and then you went back 567 \cfrac{3}{4} more, you are further down the negative side of the number line.
-34 \cfrac{2}{3}+\left(-567 \cfrac{3}{4}\right)=-602 \cfrac{5}{12}
Teaching tips for addition and subtraction
- Sufficient time using place value blocks, 100 s charts, grids and other interactive manipulatives should be provided to students when they are first learning to operate with any new set of numbers. The Common Core Standards intentionally allow time for students to develop an understanding of the operation, before learning how to use the algorithm.
- When students are first learning, encourage them to make connections between addition problems and subtraction problems. As students learn how to operate with any new set of numbers (whole, integer, or rational), it is crucial that they see the connection, as this opens the door to solving strategies, helps them make sense of the algorithms, and can be used to decide if an answer is reasonable. Understanding this relationship is also important for later topics like solving equations.
- When choosing printable math worksheets, look for resources that have missing numbers in all parts of the equation (start unknown, change unknown, result unknown). This helps students develop flexible ideas about the operations and can help prevent mindlessly grabbing numbers from word problems.
- Instead of giving students subtraction worksheets that have dozens of questions to solve, prioritize worksheets that allow students to solve in more than one way and that encourage them to consider the reasonableness of their answer. While there may be times that students are expected to solve in a larger quantity (for example, when learning the algorithm or completing a math review packet), the majority of student work should focus on depth not breadth.
Easy mistakes to make
- Not considering the place value of numbers when solving
When using strategies to solve, students may choose a strategy they do not fully understand, causing them to misuse place value.
For example,
56 + 78
Thinking that they can just add 5+6+7+8.
- Thinking subtraction always leads to a smaller number (and vice versa with addition)
Students often create this false idea because subtracting a larger number from a smaller number or adding negative numbers are not addressed in elementary school. As students begin to operate with integers, it is important to consistently ask them to make sense of an equation before operating. This may be explaining the operation in their own words or using a model to show what is happening.
- Combining two positive or two negative to make a zero pair
If students do not understand why a positive and negative value combine to be 0, they can use the zero pair strategy incorrectly.
For example,
Thinking for -4 + (-2) means that there are zero pairs formed, and the answer is -2.
In this case, there are no zero pairs formed because there are no positives to match with the negatives.
-4+(-2)=-6
- Not making sense of operations with rational numbers
By the time students operate with rational numbers, they will have learned many algorithms. Though algorithms can be useful, if used in a rush it is easy to make mistakes. Encourage students to think about a reasonable answer before solving. This can help them catch mistakes.
Practice addition and subtraction questions
1. Solve 39 + 46.




You can use a model of the tens and ones.
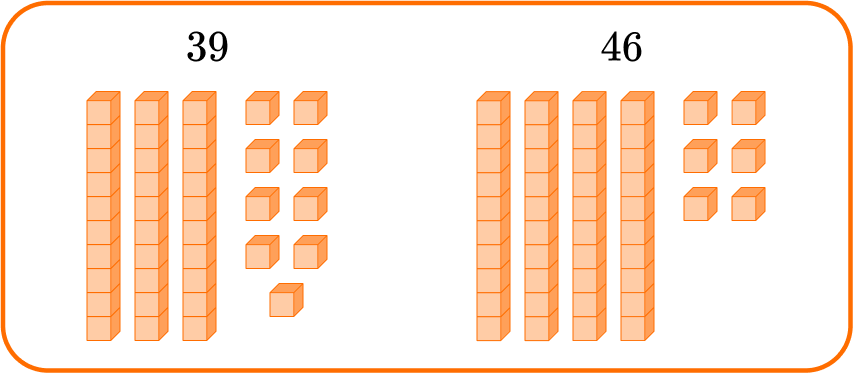
Combine the tens and ones.

You can create one new group of ten from 10 ones.
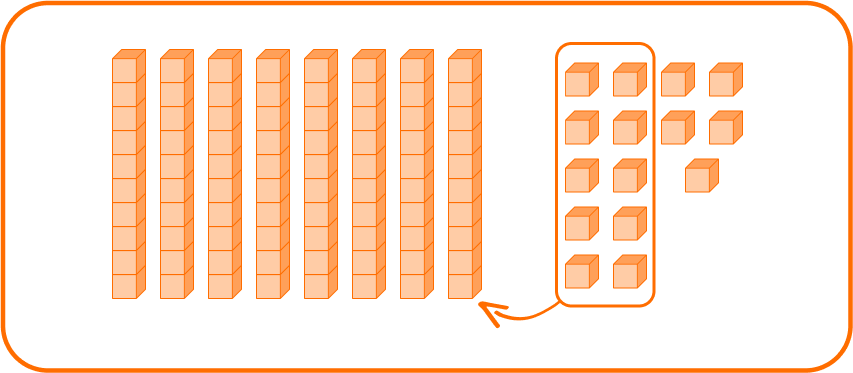
This leaves 8 tens and 5 ones, which is 85.
39+46=85
2. Solve 763-594.




You can use a number line to count up to 594 from 763.
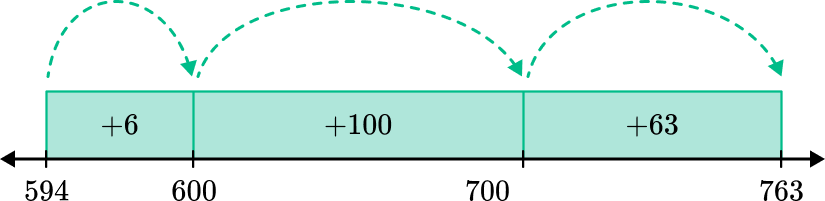
The difference between 594 and 763 is 169.
So, 763-594=169.
3. Solve 5,621 + 3,570.




To use the standard algorithm, stack the numbers and line up the place values.

You can estimate to decide if your answer is reasonable.
5,621 rounds to 6,000.
3,570 rounds to 4,000.
6,000+4,000=10,000, so the answer should be close to 10,000.
Since 9,191 is close, the answer is reasonable.
5,621+3,570=9,191
4. Jerome has 18,341 points in a game. Yasmine has 8,239 points in the same game. How many more points does Jerome have?




18,341-8,239 = ⬜
To solve with the standard algorithm, stack the numbers and line up the place values.
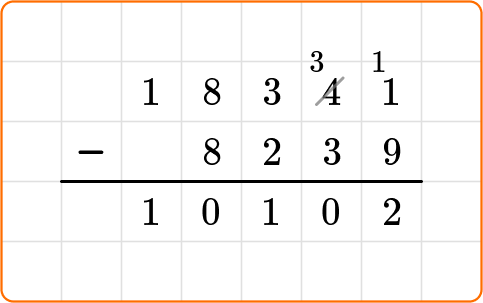
You can estimate to decide if your answer is reasonable.
18,341 rounds to 18,000.
8,239 rounds to 8,000.
18,000-8,000=10,000, so the answer should be close to 10,000.
Since 10,102 is close, the answer is reasonable.
18,341-8,239=10,102
5. Subtract: -12-3= \, ?




-12-3 starts with -12 and removes 3 positives. Add 3 zero pairs in order to remove 3.

There are 15 negative counters left.
You can also think of this as the distance from 3 to -12.
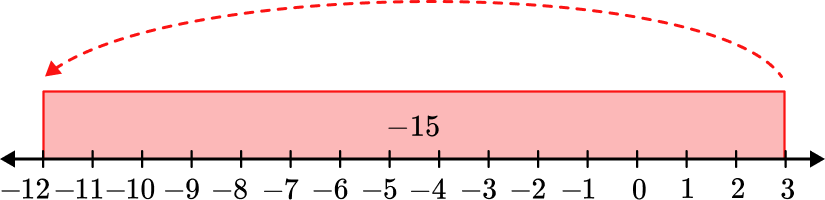
-12-3=-15
6. Solve -84.4+391.02= \, ?.




-84.4 + 391.02 combines negative and positive values, which creates zero pairs. This means that -84.4+391.02=391.02-84.4, so you can use the standard algorithm to solve.
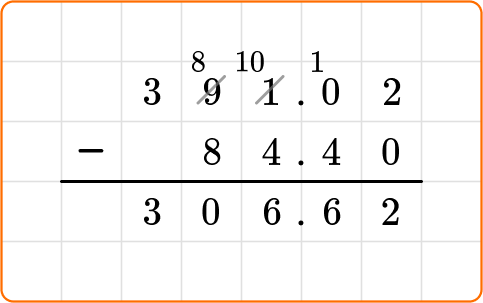
Adding a smaller negative number to a larger positive results in a positive answer.
-84.4+321.02=306.62
Addition and subtraction FAQs
Regrouping is when you are adding and have more than 10 ones, tens, hundreds, etc. and you need to regroup to create a new group of ten, hundred, etc.
For example, if you add 27 + 18, you will have 3 tens and 15 ones. You regroup 10 of the ones to be a new group of ten, so you are left with 4 tens and 5 ones, or 45.
Exchanging is when you are subtracting and you do not have enough ones, tens, hundreds, etc. to take away and you need to exchange for a new group of ten, hundred, etc.
For example, if you subtract 27 - 18, you start with 7 ones and need to take away 8. There are not enough, so you exchange one of the tens in 27 for ones. Then you have 1 ten and 17 ones. Now you can subtract 8 ones from 17 ones, leaving 9 ones.
In 4 th grade students learn to add and subtract fractions with common denominators. In fifth grade they learn to add and subtraction fractions with uncommon denominators. Then in 7 th grade they are expected to add and subtract negative fractions.
See also: Adding and subtracting fractions
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!