High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Pythagorean theorem Rearranging equations SOHCAHTOA Fractions Polynomial Factoring Linear equationsTrig functions
Here you will learn what the trigonometric functions and inverse trigonometric functions are and how you can use them to calculate missing side lengths and angles in right triangles.
Students will first learn about trig functions as part of geometry in high school.
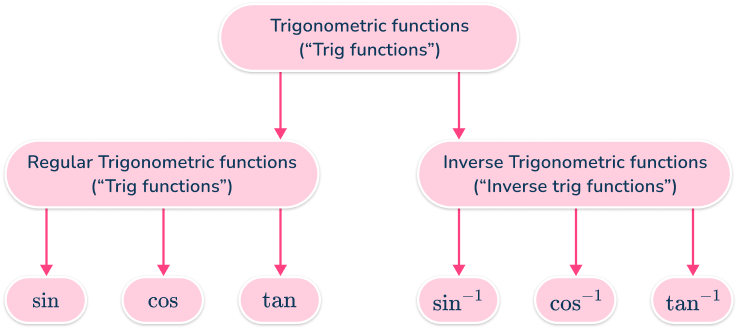
What are trig functions?
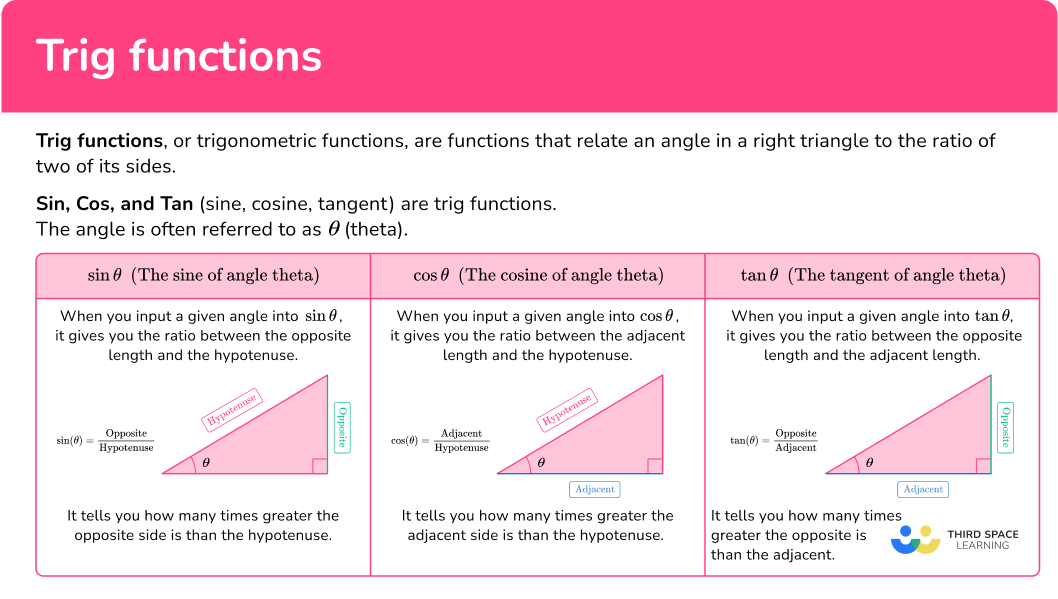
Trig functions, or trigonometric functions, are functions that relate an angle in a right triangle to the ratio of two of its sides.
Sin, Cos, and Tan (sine, cosine, tangent) are trig functions.
The angle is often referred to as theta and is represented using the symbol \theta.
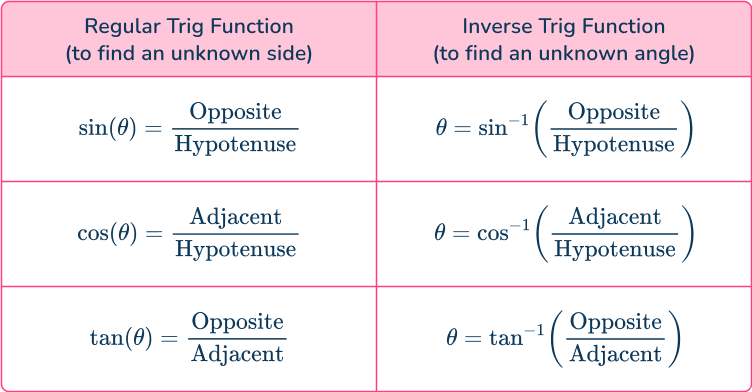
sin θ (The sine of angle theta)
When you input a given angle into \sin\theta, it gives you the ratio between the opposite length and the hypotenuse.
It tells you how many times greater the opposite side is than the hypotenuse.
\sin(\theta)=\cfrac{\text{Opposite}}{\text{Hypotenuse}}
![[FREE] Trigonometry Worksheet (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
[FREE] Trigonometry Worksheet (Grade 9 to 12)
![[FREE] Trigonometry Worksheet (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 9 to 12 students’ understanding of Trigonometry. 15+ questions with answers covering a range of 9th to 12th grade trigonometry topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Trigonometry Worksheet (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
[FREE] Trigonometry Worksheet (Grade 9 to 12)
![[FREE] Trigonometry Worksheet (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 9 to 12 students’ understanding of Trigonometry. 15+ questions with answers covering a range of 9th to 12th grade trigonometry topics to identify areas of strength and support!
DOWNLOAD FREEcos θ (The cosine of angle theta)
When you input a given angle into \cos\theta , it gives you the ratio between the adjacent length and the hypotenuse.
It tells you how many times greater the adjacent side is than the hypotenuse.
\cos(\theta)=\cfrac{\text{Adjacent}}{\text{Hypotenuse}}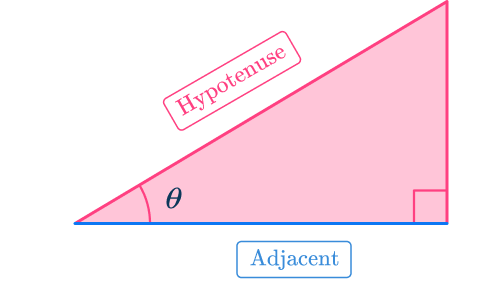
tan θ (The tangent of angle theta)
When you input a given angle into \tan\theta , it gives you the ratio between the adjacent length and the opposite length.
It tells you how many times greater the opposite is than the adjacent.
\tan(\theta)=\cfrac{\text{Opposite}}{\text{Adjacent}}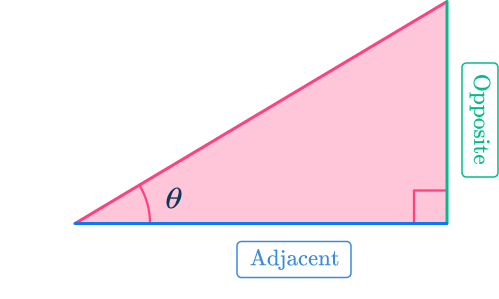
In summary, trigonometric functions can tell you how many times greater one side is than another in triangles containing a right angle. Therefore, if you are given the length of one side and the value of one angle, you can set up equations using trigonometric functions to help you find the lengths of the other sides.
Alternatively, if you are given the length of two sides of a right triangle, you can determine the size of the respective angle. This is calculated using inverse trigonometric functions.
What are inverse trigonometric functions?
In the same way that addition and subtraction are inverse operations, inverse trig functions do the opposite of regular trig functions.
You can use the inverse sine function, the inverse cosine function, and the inverse tangent function to find the missing angle \theta.
The inverse trig functions are:

The regular trig functions are functions that act on an angle \theta.
As these functions are equal to the ratio of two respective side lengths, the inverse trig functions act on this ratio, not the angle.
It is important to note that “trig functions” is an overarching term for all trigonometric functions, including inverse trigonometric functions. This means that “inverse trig functions” can be used interchangeably with “trig functions”.
What are trig functions?
What are trig functions?

Common Core State Standards
How does this relate to high school math?
- High School – Geometry – Similarity, Right Triangles, & Trigonometry (HS.G.SRT.C.6)
Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.
- High School – Geometry – Similarity, Right Triangles, & Trigonometry (HS.G.SRT.C.8)
Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
How to use trigonometric functions
In order to use trigonometric functions:
- Label one angle in the right triangle that is known/required. This cannot be the right-angle.
- Label the side lengths with respect to the known/required angle and reject one side that is unknown/not useful.
- Set up an equation involving the correct trig function.
- Rearrange the equation so the subject is the value you are going to find.
- Find the answer using a calculator and round it as needed.
- Write the answer with the correct units.
Trig functions examples
Example 1: calculating with trigonometric functions
Find the value of x, given \sin(72)=\cfrac{25}{x}. Give your answer to the nearest tenth.
- Label one angle in the right triangle that is known/required. This cannot be the right-angle.
You already have an equation involving \sin , so there is no angle to label.
2Label the side lengths with respect to the known/required angle and reject one side that is unknown/not useful.
You already have an equation involving \sin , so there is no angle to label.
3Set up an equation involving the correct trig function.
The given equation is \sin(72)=\cfrac{25}{x} .
4Rearrange the equation so the subject is the value you are going to find.
Multiply both sides of the equation by x first.
x\times\sin(72)=25Divide both sides of the equation by \sin(72) .
x=\cfrac{25}{\sin(72)}5Find the answer using a calculator and round it as needed.
Type \cfrac{25}{\sin(72)} into a calculator to find x.
x=\cfrac{25}{\sin(72)}=26.28655561=26.2 (nearest tenth)
6Write the answer with the correct units.
There are no units stated, however it is important to note that the value of x would represent a length and so units may be \mathrm{cm, km, in} etc, not an angle with the units ^{\circ}.
Example 2: finding the length of a side
Find the length labeled x in the triangle below. Give your answer to 3 significant figures.
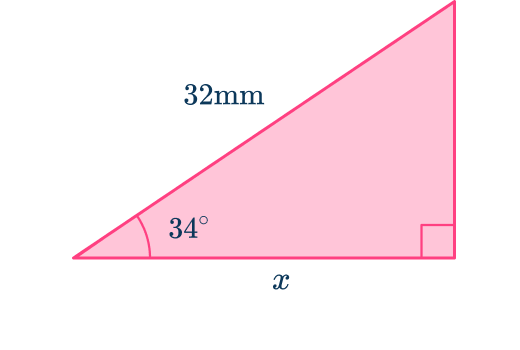
Label one angle in the right triangle that is known/required. This cannot be the right-angle.
The known angle that is not the right angle is 34^{\circ}.
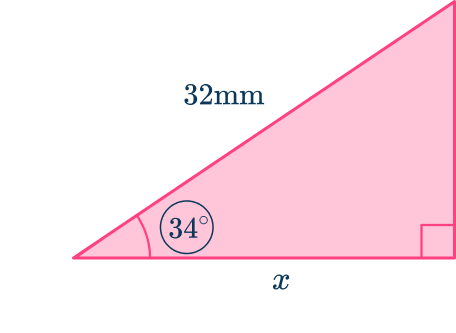
Label the side lengths with respect to the known/required angle and reject one side that is unknown/not useful.
Labeling the triangle, you can see that you know the hypotenuse H and you want to know the adjacent, A. Reject the opposite side labeled O. The trigonometric function which compares these two sides is \cos.
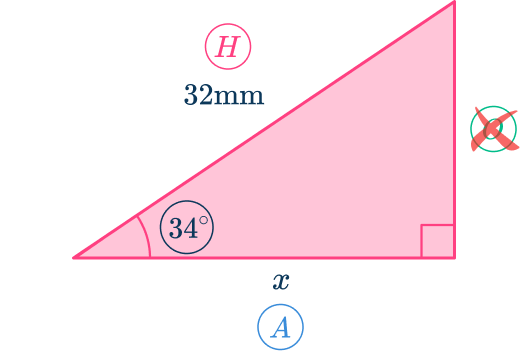
Set up an equation involving the correct trig function.
You know that \cos(\theta)=\cfrac{\text{Adjacent}}{\text{Hypotenuse}} , therefore \cos(34)=\cfrac{x}{32}.
Rearrange the equation so the subject is the value you are going to find.
Multiply both sides of the equation by 32 .
32\times\cos(34)=x
Find the answer using a calculator and round it as needed.
Write the answer with the correct units.
Example 3: finding the length of a side
Find the length labeled x in the triangle below. Give your answer to 3 significant figures.
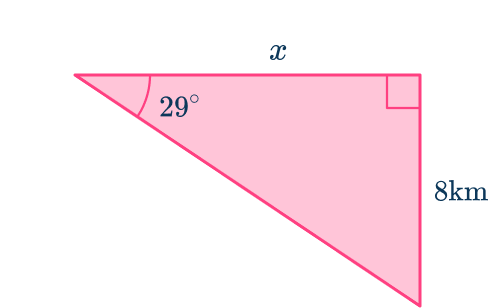
Label one angle in the right triangle that is known/required. This cannot be the right-angle.
The known angle that is not the right angle is 29^{\circ}.
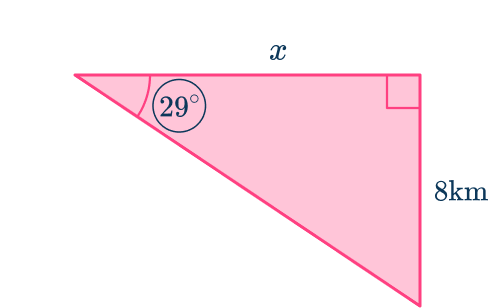
Label the side lengths with respect to the known/required angle and reject one side that is unknown/not useful.
Labeling the triangle, you can see that you know the opposite and you want to know the adjacent. The trigonometric function which compares these two sides is \tan.
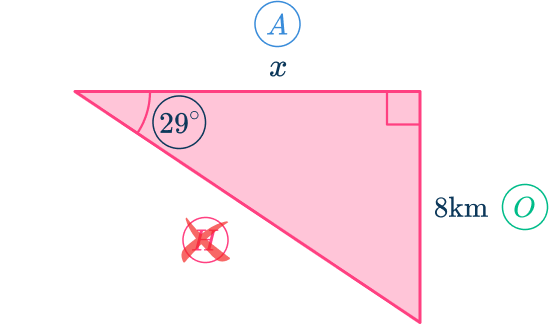
Set up an equation involving the correct trig function.
You know that \tan(\theta)=\cfrac{\text{Opposite}}{\text{Adjacent}} , therefore \tan(29)=\cfrac{8}{x}.
Rearrange the equation so the subject is the value you are going to find.
Multiply both sides of the equation by x .
x\times\tan(29)=8
Divide both sides of the equation by \tan(29) .
x=\cfrac{8}{\tan(29)}
Find the answer using a calculator and round it as needed.
Write the answer with the correct units.
Example 4: use inverse trigonometric functions
Find the value of \theta to the nearest tenth.
\sin(\theta)=0.9Label one angle in the right triangle that is known/required. This cannot be the right-angle.
You already have an equation involving \sin so there is no angle to label.
Label the side lengths with respect to the known/required angle and reject one side that is unknown/not useful.
You already have an equation involving \sin , so there is no angle to label.
Set up an equation involving the correct trig function.
\sin(\theta)=0.9 is already in the required form.
Rearrange the equation so the subject is the value you are going to find.
Here, the question requires you to find the angle \theta. As the sine function is currently acting on \theta , use the inverse sine function on both sides of the equation to make \theta the subject.
\begin{aligned}\sin^{-1}(\sin(\theta))&=\sin^{-1}(0.9) \\\\ \theta&=\sin^{-1}(0.9) \end{aligned}
Note: See the practical analogy at the end of the example for help with understanding why \sin^{-1}(\sin(\theta))=\theta
Find the answer using a calculator and round it as needed.
\theta=64.15806724=64.2 (nearest tenth)
Write the answer with the correct units.
A useful analogy to help understand \sin^{-1}(\sin(\theta))=\theta\text{:}
Imagine throwing a ball straight up in the air, and then catching it in exactly the same place the ball started.
Here, the ball is \theta.
Let the function \sin represent throwing the ball (\theta).
Let the function \sin^{-1} represent catching the ball (\theta).
Throwing the ball is an action on the ball. Catching the ball is the opposite action on the ball. If you throw the ball, then catch the ball in exactly the same place, nothing about the ball or its position have changed as both of the acts on the ball have canceled each other out. In essence, nothing has happened.
So catch(throw(ball)) = ball or \sin^{-1}(\sin(\theta))=\theta
Example 5: use inverse trigonometric functions
Find the value of \theta to the nearest hundredth when 2\cos(\theta)=0.8.
Label one angle in the right triangle that is known/required. This cannot be the right-angle.
You already have an equation involving \cos , so there is no angle to label.
Label the side lengths with respect to the known/required angle and reject one side that is unknown/not useful.
You already have an equation involving \cos , so there are no side lengths to label.
Set up an equation involving the correct trig function.
You have the equation 2\cos(\theta)=0.8
Rearrange the equation so the subject is the value you are going to find.
You want to isolate \theta on one side of the equation, so first divide both sides of the equation by 2.
\cos(\theta)=0.4
Apply the inverse cosine trigonometric function to each side of the equation to make \theta the subject.
\theta=\cos^{-1}(0.4)
Find the answer using a calculator and round it as needed.
\theta=66.42182152=66.42 (nearest hundredth)
Write the answer with the correct units.
\theta=66.42^{\circ} (nearest hundredth)
Example 6: calculate an angle in a triangle
Calculate the unknown angle x to 1 significant figure.
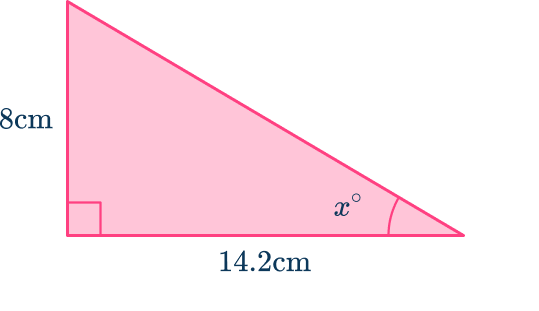
Label one angle in the right triangle that is known/required. This cannot be the right-angle.
The required angle is x^{\circ}.
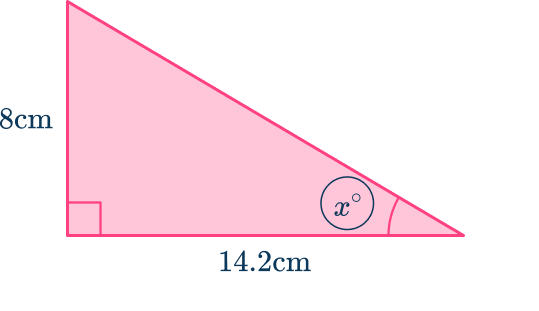
Label the side lengths with respect to the known/required angle and reject one side that is unknown/not useful.
Labeling the triangle, you can see that you know the opposite and you know the adjacent. The trigonometric function which compares these two sides is \tan.
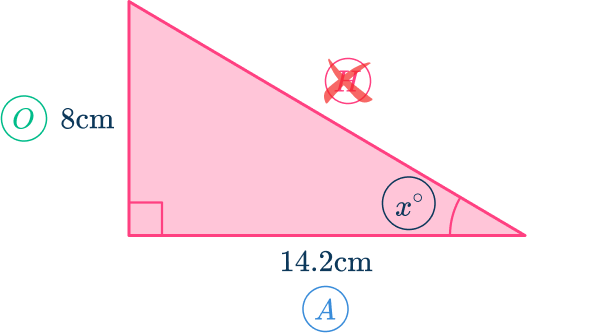
Set up an equation involving the correct trig function.
You know that \tan(x)=\cfrac{\text{Opposite}}{\text{Adjacent }}
So, \tan(x)=\cfrac{8}{14.2}
Rearrange the equation so the subject is the value you are going to find.
Apply the inverse tangent trigonometric function to each side of the equation to make x the subject.
x=\tan^{-1}\left(\cfrac{8}{14.2}\right)
Find the answer using a calculator and round it as needed.
Write the answer with the correct units.
You can check that the answer is sensible here. All angles (other than the right angle) in a right triangle should be acute angles. 30^{\circ} is acute therefore the answer is sensible.
Teaching tips for trig functions
- Introduce the unit circle to explain how the values of sine and cosine change as the angle increases. Stress that the radius of the unit circle is 1, so sine and cosine are just the y – and x -coordinates of a point on the circle.
- Once students are familiar with the basic trigonometric functions, connect them to the Pythagorean identities. Show the derivation of \sin^{2}(\theta)+\cos^{2}(\theta)=1 from the Pythagorean theorem, reinforcing the geometric origins of trigonometry.
- Emphasize symmetry in trigonometric functions, such as how sine is an odd function and cosine is even. Show students the periodic nature of these functions and how they repeat every 360^{\circ}.
Easy mistakes to make
- Using the wrong function
You use sin, cos, and tan to find side lengths and inverse sin, inverse cos, and inverse tan to find angles.
- Not knowing other trig identities
There are other trigonometric identities as well as sin, cos, and tan, called reciprocal identities. These include the cosecant function, the secant function and the cotangent function.
\cfrac{1}{\sin\theta}=\mathrm{cosecant} \, \theta\text{ (or }\csc\theta)
\cfrac{1}{\cos\theta}=\mathrm{secant} \, \theta\text{ (or }\sec\theta)
\cfrac{1}{\tan\theta}=\mathrm{cotangent} \, \theta\text{ (or }\cot\theta)
- Thinking \bf{\sin^{-1}(\theta)} mean \bf{\cfrac{1}{\sin(\theta)}}
Raising a variable or number to the power of - \, 1 refers to the reciprocal ( 1 over the number). For example, x^{-1}=\cfrac{1}{x}, \quad 5^{-1}=\cfrac{1}{5} etc.
Raising a function to the power of - \, 1 refers to the inverse of the function.
For example, f^{-1}(x) refers to the inverse of the function f(x), \sin^{-1}(x) refers to the inverse of the function \sin(x).
Referring to:- \sin^{-1}(x) as \arcsin(x)
- \cos^{-1}(x) as \arccos(x)
- \tan^{-1}(x) as \arctan(x)
avoids this confusion!
- Using degrees instead of radians (or vice versa)
Encourage students to always check whether they are working in degrees or radians. Using a visual unit circle for both units can help solidify the connection.
- Forgetting to change signs depending on the quadrant
Students may forget that trigonometric functions change signs depending on the quadrant (for example, sine is positive in the 1 st and 2 nd quadrants but negative in the 3 rd and 4 th).
Related trigonometry lessons
Practice trig functions questions
1. Find the value of x when \tan{42}=\cfrac{x}{5}, giving your answer to the nearest tenth.




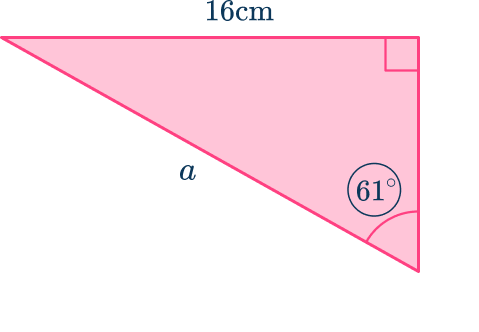
2. Find the length of the side labeled a on this triangle, giving your answer to 2 significant figures.
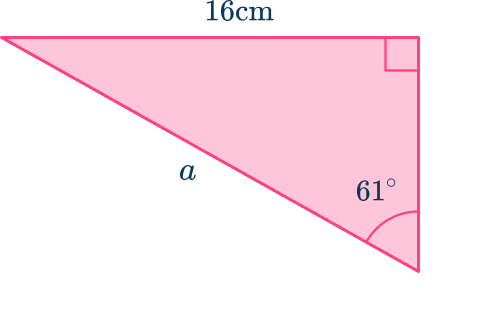




Label the known angle that is not the right angle:
Label the side lengths, reject the irrelevant side:
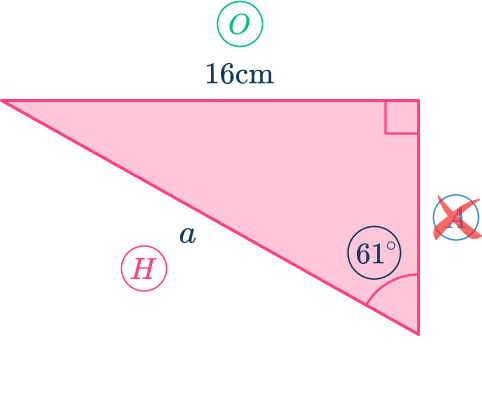
The trigonometric function involving the opposite side and the hypotenuse is \sin\theta=\cfrac{O}{H}.
As O=16\mathrm{~cm}, \, H=a and \theta=61^{\circ}
\sin(61)=\cfrac{16}{a}.
Rearranging this you get
\begin{aligned}a\times\sin(61)&=16 \\\\ a&=\cfrac{16}{\sin(61)}=18.3\text{ (2sf)} \end{aligned}
3. Find the length AB. Give your answer to the nearest hundredth.





Label the known angle that is not the right angle:

Label the side lengths, reject the irrelevant side:
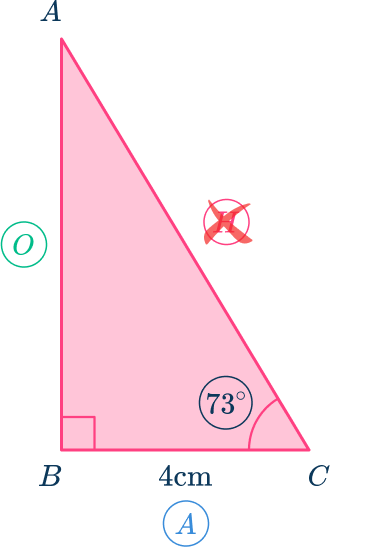
The trigonometric function involving the opposite side and the adjacent side is \tan\theta=\cfrac{O}{A}.
As O=AB, \, A=4\mathrm{~cm} and \theta=73^{\circ}
\tan(73)=\cfrac{AB}{4}.
Rearranging this you get
\begin{aligned}4\times\tan(73)&=AB \\\\ AB&=13.08\text{ (2dp)} \end{aligned}
4. Find the value of x when \cos(x)=0.2. Give your answer to the nearest tenth.




\cos(x)=0.2 so x=\cos^{-1}(0.2)=78.5^{\circ} (nearest tenth)
5. Solve the equation \sin(\theta)+5=5.7. Give your answer to the nearest tenth.




6. Find the value of \theta in the triangle below. Give your answer to the nearest tenth.
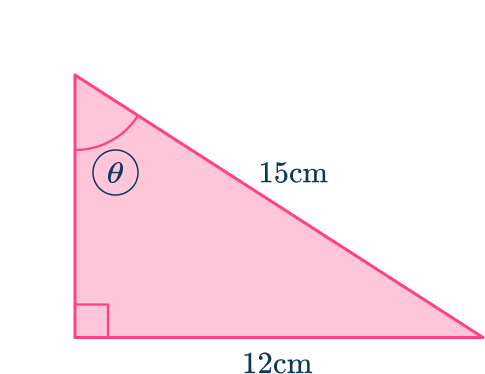




First you need to label the required sides and angles, and set up the equation using SOHCAHTOA.
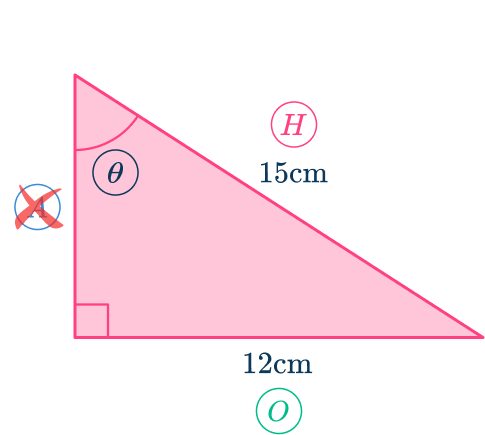
You know the opposite and the hypotenuse so you need to use \sin.
\begin{aligned}\sin(\theta)&=\cfrac{O}{H} \\\\ \sin(\theta)&=\cfrac{12}{15} \\\\ \theta&=\sin^{-1}\left(\cfrac{12}{15}\right) \\\\ \theta&=53.1^{\circ}\text{ (nearest tenth)} \end{aligned}
Trig functions FAQs
The three basic trigonometric functions are sine (\sin), cosine (\cos), and tangent (\tan).
The reciprocal functions are cosecant (\csc), secant (\sec), and cotangent (\cot).
The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane.
Trig functions for an angle \theta can be defined using the coordinates of points on the unit circle:
° \sin (\theta) is the y -coordinate
° \cos (\theta) is the x -coordinate
The unit circle also helps determine values of trig functions for any angle, not just those in a right triangle.
Periodic functions repeat their values at regular intervals, called the period.
Trigonometric functions like sine and cosine are periodic because their values repeat every 360^{\circ}, while tangent repeats every 180^{\circ}.
This periodicity is key to understanding the cyclical nature of trig functions.
The next lessons are
- Circle math
- Angles of a circle
- Circle theorems
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!