Circumference of a Circle - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

2D shapes Irrational numbers Rounding decimals

Math resources Geometry

Circle math

Circumference of a circle

Here you will learn about calculating the circumference of a circle including how to calculate the circumference of a circle given the circle’s radius, diameter, or area, how to calculate the perimeter of a semi-circle, and how to calculate the radius or diameter of a circle given the circumference.

Students will first learn about circumference of a circle as part of geometry in $7$ th grade.

What is the circumference of a circle?

Circumference of a circle is the distance around the circle. It can also be known as the perimeter of a circle, but circumference is a special case of perimeter.

Both describe the total length of the boundary of a two-dimensional shape, but circumference specifically refers to the perimeter of a curved figure or arc. Therefore it only applies to circles, ovals, ellipses, arcs, etc.

Circumference of a circle formula:

There is a specific relationship between the diameter of a circle and its circumference.

If you multiply the diameter of a circle by $\pi$ , you will calculate the length of the circumference. This is true of all circles.

Therefore this formula can be used to find the circumference of any given circle:

$\pi \times d$

As the diameter of the circle is twice the radius, you can also use this formula:

$2\times\pi \times r$

Which formula you use will depend on whether you know the circle’s diameter or the circle’s radius.

For example,

What is the circumference of a circle with radius $3~{cm}?$

\begin{aligned} \text { Circumference } &=2 \times \pi \times r \\\\ &=2 \times \pi \times 3 \\\\ &=6 \pi \mathrm{~cm} \\\\ &=18.8 \mathrm{~cm} \text { (to the nearest tenth) } \end{aligned}

\begin{aligned} \text { Circumference } &=\pi \times d \\\\ &=\pi \times 6 \\\\ &=6 \pi \mathrm{~cm} \\\\ &=18.8 \mathrm{~cm} \text { (to the nearest tenth) } \end{aligned}

What is the circumference of a circle?

Common Core State Standards

How does this relate to $7$ th grade math?

Grade 7 – Geometry (7.G.B.4)
Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.

[FREE] 2D Shape Check for Understanding Quiz (Grade 2 to 4)

Use this quiz to check your grade 2 – 4 students’ understanding of 2D shape. 10+ questions with answers covering a range of 2nd, 3rd and 4th grade 2D shape topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] 2D Shape Check for Understanding Quiz (Grade 2 to 4)

DOWNLOAD FREE

How to calculate the circumference of a circle

In order to calculate the circumference of a circle:

Find the radius or diameter of the circle.
Use the relevant formula to calculate the circumference of the circle.
Give your answer clearly with the correct units.

Circumference of a circle examples

Example 1: calculating the circumference of the circle given the radius

A circle has a radius of $6~{cm}.$

Calculate its circumference.

Give your answer to the nearest tenth.

Find the radius or diameter of the circle.

The radius is given in the question.

Radius $= 6~{cm}$

2Use the relevant formula to calculate the circumference of the circle.

In this question you have the radius, therefore you should use the formula,

2\times\pi \times r

2\times\pi \times 6

12\pi

37.699911\dots

Remember, the question asks you to round your answer to the nearest tenth.

37.7

3Give your answer clearly with the correct units.

Remember, circumference is a measure of length; therefore, the units should not be “squared.”

37.7~{cm}

Example 2: calculating the circumference of the circle given the diameter

A circle has a diameter of $10~{mm}.$

Calculate its circumference.

Give your answer to the nearest tenth.

Find the radius or diameter of the circle.

In this question, the question gives you the diameter.

Diameter $= 10~{mm}$

Use the relevant formula to calculate the circumference of the circle.

\pi \times d

$\pi \times 10$

$10\pi$

$31.41592\dots$

Remember, the question asks you to round your answer to the nearest tenth.

$31.4$

Give your answer clearly with the correct units.

31.4~{mm}

Example 3: calculating the circumference of the circle, given the radius, answer in terms of 𝝅.

A circle has a radius of $8~{m}.$

Calculate its circumference.

Give your answer in terms of $\pi.$

Find the radius or diameter of the circle.

The radius is given in the question.

Radius $= 8~{m}$

Use the relevant formula to calculate the circumference of the circle.

In this question you have the radius, therefore you should use the formula,

$2\times\pi \times r$

$2\times\pi \times 8$

$16\pi$

Remember, the question asks you to give your answer to $‘$ in terms of $\pi’.$ Therefore, you leave the answer in the form $16\pi.$

Give your answer clearly with the correct units.

16\pi~{m}

Example 4: calculating the circumference of the circle given the diameter

A circle has a diameter of $420~{km}.$

Calculate its circumference.

Give your answer in terms of $\pi.$

Find the radius or diameter of the circle.

In this question, the question gives you the diameter.

Diameter $= 10~{mm}$

Use the relevant formula to calculate the circumference of the circle.

\pi \times d

$\pi \times 420$

$420\pi$

Remember, the question asks you to give your answer to $‘$ in terms of $\pi’.$ Therefore, you leave the answer in the form $420\pi.$

Give your answer clearly with the correct units.

420\pi~{km}

Example 5: calculating the circumference of the circle given the area of a circle

A circle has an area of $21 \mathrm{~cm}^2.$

Calculate its circumference.

Give your answer to the nearest hundredth.

Find the radius or diameter of the circle.

The question gives you the area of the circle, but you need the radius/diameter in order to calculate the circumference.

You know that:

Area of a circle $= \pi r^2$

This means you can find the radius of the circle from the area.

$\text {Area }=\pi r^{2}$

$\text {Area }=21$

$21=\pi r^{2} \quad$ Divide both sides by $\pi$

$\cfrac{21}{\pi}=r^{2} \quad \;$ Square root both sides of the equation

$\sqrt{\cfrac{21}{\pi}}=\sqrt{r^{2}}$

$2.5854 \ldots=r$

Notice how you leave the answer to more decimals places than the question asks for. This is so you do not cause a rounding error later on in the question.

Use the relevant formula to calculate the circumference of the circle.

In this question you now have the radius, therefore you should use the formula,

$2\times\pi \times r$

$2\times\pi \times 2.5854$

$16.24454..$

Remember, the question asks you to round your answer to the nearest hundredth.

$16.24$

Give your answer clearly with the correct units.

16.24~{cm}

Example 6: calculating the perimeter of a semi-circle given the diameter

A semicircle has a diameter of $20~{m}.$

Calculate its perimeter.

Give your answer in terms of $\pi.$

Find the radius or diameter of the circle.

In this question, the question gives you the diameter.

Diameter $= 20~{m}$

Use the relevant formula to calculate the circumference of the circle.

\pi \times 20

$20\pi$

Remember, the question asks you to round your answer to $‘$ in terms of $\pi’.$ Therefore, you leave the answer in the form $20\pi.$

$20\pi$

This represents the circumference of a circle with a diameter of $20~{m}.$ The perimeter of the semi-circle is the length of the arc and the length of the diameter added together.

Length of Arc

The length of the arc is half that of the whole circle because it is a semi-circle.

Therefore, the length of the arc is $20\pi$ divided by $2.$

Length of arc $=10\pi$

Length of Diameter

Given to you in the question, $20~{m}.$

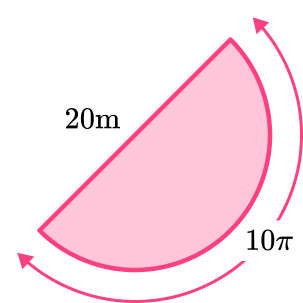
Perimeter of the circle

Length of Arc $+$ Length of Diameter

$10\pi+20$

Remember to keep it in terms of $\pi$ as stated in the question.

Give your answer clearly with the correct units.

10\pi+20~{m}

Teaching tips for circumference of a circle

Before diving into the circumference formula, ensure that students have a solid understanding of the basic concepts such as radius and diameter. Use visual aids like diagrams to illustrate these concepts and provide step by step guidance to students who need it.

Provide practice problems that show real-life examples where understanding the circumference of a circle is important, such as measuring the distance around a circular object like a pizza, a clock, or a bicycle wheel. This helps students see the practical applications of the concept.

Engage students with hands-on activities instead of worksheets. For example, have them measure the circumference of objects in the classroom using a string or measuring tape. This kinesthetic approach can enhance understanding.

Easy mistakes to make

Not including the correct units
When working with circumference, give the correct units; they should not be squared.
For example, $cm, m, km$ etc.

Not rounding correctly
These types of questions often involve rounding. Only round at the end of the question and ensure you are rounding to what the question specifies.

Not giving an answer in terms of 𝝅
Sometimes the question may ask you to give the answer $‘$ in terms of $\pi’.$ This means you do not give the numerical answer that is produced when you multiply it by $\pi.$
For example,
$6 \times \pi = 6\pi$ (this is an answer in terms of pi)
$6 \times \pi = 18.8495592…$ (this answer is not in terms of pi since $6$ was multiplied by the value of pi)

Misuse of a calculator
Ensure you know how to correctly use the $\pi$ button on your calculator when using one for a circumference calculation.

Practice circumference of a circle questions

18.8~{cm}

6 \pi \mathrm{~cm}^2

18.8~{m}

6 \pi \mathrm{~cm}

\begin{aligned} & \pi \times d \\\\ & =\pi \times 6 \\\\ & =6 \pi \mathrm{~cm} \end{aligned}

18.8~{cm}

6 \pi \mathrm{~cm}^2

18.8~{m}

6 \pi \mathrm{~cm}

\begin{aligned} & \pi \times d \\\\ & =\pi \times 6 \\\\ & =18.849 \ldots \mathrm{~cm} \end{aligned}

$18.8 \mathrm{~cm}$ (rounded to the nearest tenth)

31.4 \pi \mathrm{~cm}^2

20 \mathrm{~m}^2

10\pi~{cm}

24.5

Circumference is a measure of length and this is the only answer with a measure of length $(cm)$ as its units.

\pi \mathrm{~cm}^2

\pi \mathrm{~cm}

6.3~{cm}

6.28~{cm}

\begin{aligned} & 2 \times \pi \times \mathbf~{r} \\\\ & =2 \times \pi \times \mathbf~{1} \\\\ & =6.2831 \ldots \mathrm{cm} \\\\ & =6.3 \mathrm{~cm} \end{aligned}

(rounded to the nearest tenth)

2 \pi \mathrm{~cm}^2

2 \pi \mathrm{~cm}

6.3~{cm}

6.28~{cm}

\begin{aligned} & 2 \times \pi \times \mathbf{r} \\\\ & = 2 \times \pi \times 1 \\\\ & = 2 \pi \mathrm{~cm} \end{aligned}

This answer has been left in terms of $\pi.$

4 \pi \mathrm{~cm}

\pi \mathrm{~cm}

12.7~{cm}

12.7 \mathrm{~cm}^2

\begin{aligned} & \pi \times \mathrm{d} \\\\ & =\pi \times 4 \\\\ & =4 \pi \mathrm{~cm} \end{aligned}

628.3 \mathrm{~cm}^2

629 \mathrm{~cm}

628~{cm}

200 \pi \mathrm{~cm}

\begin{aligned} & 2 \times \pi \times \mathrm{r} \\\\ & =2 \times \pi \times 100 \\\\ & =628.3185 \ldots \mathrm{cm} \\\\ & =628 \mathrm{~cm} \end{aligned}

(rounded to the nearest integer)

Remember, integer means whole number.

Circumference of a circle FAQs

How do you find the circumference of a circle?

The circumference of a circle is found using the formula
$2 \times \pi \times r$ or $\pi \times d,$ where $\pi$ is a mathematical constant with an approximate value of $3.14, r$ is the radius, and $d$ is the diameter.

How do you find the circumference using the radius of a circle?

To find the circumference of a circle with radius $r,$ you would use the formula $2 \times \pi \times r.$

What is the difference between circumference and perimeter?

Circumference specifically applies to the distance around the outer edge of a circle while perimeter is a more general term used for any closed two-dimensional shape, including polygons with straight sides. The formulas used to calculate circumference and perimeter depend on the specific shape.

What is the circumference of the earth?

The approximate circumference of the Earth is about $40,075$ kilometers ( $24,901$ miles).

How is pi related to the circumference of a circle?

Pi, or mathematical constant $\pi,$ represents the ratio of the circumference to its diameter. This relationship is expressed by the formulas $2 \times \pi \times r$ and $\pi \times d.$

What is the difference between circumference and arc length?

The circumference of a circle is the total distance around its outer edge, while the arc length is the distance along a specific part of the circle defined by a central angle.

The next lessons are

Angles of a circle
Circle theorems
Prism shape

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.