High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Parts of a circle Polygons Irrational numbers Rounding decimals

Rounding to significant figures

Math resources Geometry

Circle math

Area of a Circle

Area of a circle

Here you will learn about calculating the area of a circle, including how to calculate the area of a circle given the radius, how to calculate the area of a circle given the diameter and how to calculate the area of a circle given the circumference.

Students will first learn about the area of a circle as a part of geometry in $7$ th grade and will expand on their knowledge into high school.

What is the area of a circle?

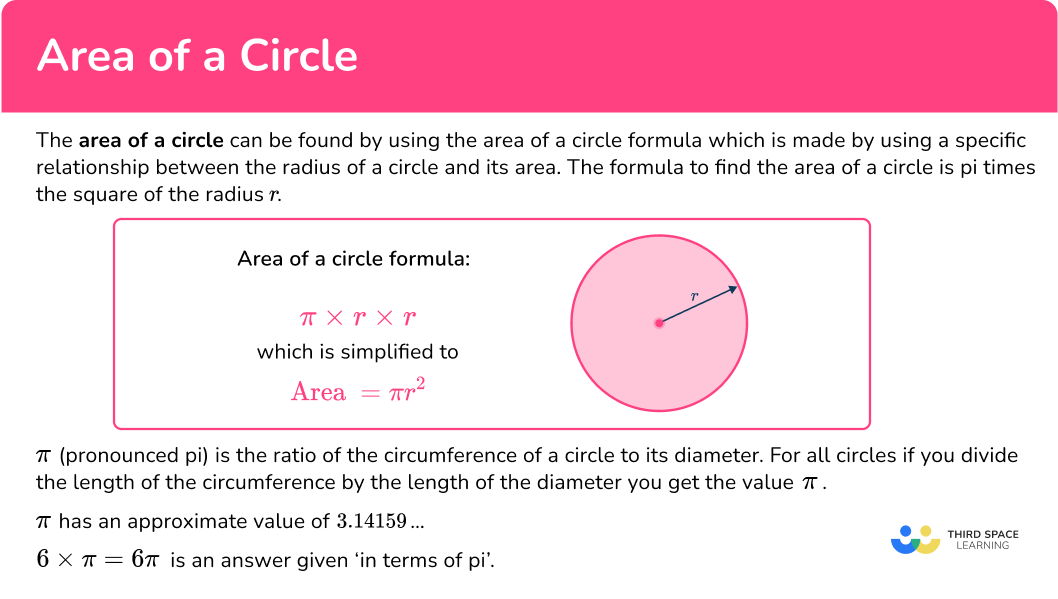
The area of a circle can be found by using the area of a circle formula which is made by using a specific relationship between the radius of a circle and its area. The formula to find the area of a circle is pi times the square of the radius $r.$

Area of a circle formula:

$\pi\times{r}\times{r}$

which is simplified to

$\text {Area}=\pi{r^2}$

For example,

What is the area of a circle with radius $3 \, cm?$

$\begin{aligned}\text {Area}&=\pi{r^2} \\\\ &=\pi\times{3^2} \\\\ &=9\pi\mathrm{~cm}^{2} \\\\ &=28.3\mathrm{~cm}^{2} \text{ (1 dp)} \end{aligned}$

What is pi?

$\pi$ (pronounced pi) represents the ratio of the circumference of a circle to its diameter. Pi is a special mathematical constant.

For all circles, if you divide the length of the circumference by the length of the diameter, you get the value $\pi.$

For example,

If the diameter of a circle was $1 \, m,$ its circumference would be $\pi \, m.$

$\pi$ is an irrational number which means it cannot be written as a fraction, and in a non recurring decimal has an approximate value of $3.14159\dots$

Sometimes the question may ask you to give the answer ‘in terms of $\pi$ ’.

This means you do not give the numerical answer when you multiply it by $\pi.$

For example, $6\times\pi=6\pi$ is an answer given in terms of pi.

What is the area of a circle?

Common Core State Standards

How does this relate to $7$ th grade math?

Grade 7: Geometry (7.G.B.4)
Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.

[FREE] Area Worksheet (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of area. 15+ questions with answers covering a range of 4th, 6th and 7th grade area topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Area Worksheet (Grade 4 to 6)

DOWNLOAD FREE

How to calculate the area of a circle

IIn order to calculate the area of a circle, you will:

Find the radius of the circle.
Use the formula $\bf{\textbf{A}=\pi \textbf{r}^2}$ to calculate the area of the circle.
State answer with the correct units.

Area of a circle examples

Example 1 : calculating the area of the circle given the radius

A circle has a radius of $6\mathrm{~cm}.$ Calculate its area. Give your answer to $2 \text{ dp}.$

Find the radius of the circle.

The length of the radius is given in the question, $r=6\mathrm{~cm}.$

2Use the formula $\bf{\textbf{A}=\pi \textbf{r}^2}$ to calculate the area of the circle.

\begin{aligned}A&=\pi{r^2} \\\\ &=\pi\times{6^2} \\\\ &=36\pi \\\\ &=113.0973355 ... \\\\ &=113.10\text{ (2 dp)} \end{aligned}

3State answer with the correct units.

113.10\mathrm{~cm}^2

Example 2 : calculating the area of the circle given the diameter

A circle has a diameter of $10\mathrm{~mm}.$ Calculate its area. Give your answer to $1 \text{ dp}.$

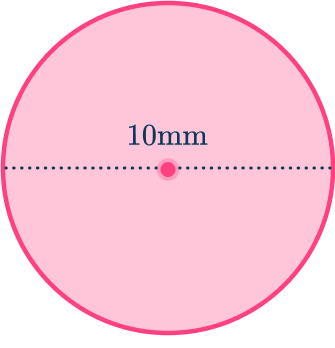
Find the radius of the circle.

The question gives you the diameter. You need the radius to find the area of the circle.

The diameter of the circle is twice the radius, the distance from the center of the circle to the boundary of the circle. Here, $d=10\mathrm{~mm}$ so

\begin{aligned}&r=10\mathrm{~mm}\div{2} \\\\ &r=5\mathrm{~mm} \end{aligned}

Use the formula $\bf{\textbf{A}=\pi \textbf{r}^2}$ to calculate the area of the circle.

\begin{aligned}A&=\pi\times{r}\times{r} \\\\ &=\pi\times{5}\times{5} \\\\ &=25\pi \\\\ &=78.53981… \\\\ &=78.5\text{ (1 dp)} \end{aligned}

State answer with the correct units.

78.5\mathrm{~mm}^2

Example 3: area of the circle, given the radius, answer in terms of π.

A circle has a radius of $8\mathrm{~m}.$ Calculate its area. Give your answer in terms of $\pi.$

Find the radius of the circle.

The radius is given in the question, $r=8\mathrm{~m}.$

Use the formula $\bf{\textbf{A}=\pi \textbf{r}^2}$ to calculate the area of the circle.

\begin{aligned}A&=\pi\times{r^2} \\\\ &=\pi\times{8^2} \\\\ &=64\pi \end{aligned}

Remember the question asks to give your answer to ‘in terms of $\pi$ ’. Therefore you leave the answer in the form $64\pi.$

State answer with the correct units.

64\pi\mathrm{~m}^2

Example 4 : calculating the area of the circle given the diameter

A circle has a diameter of $420\mathrm{~km}.$ Calculate its area. Give your answer in terms of $\pi.$

Find the radius of the circle.

The question gives you the diameter $d=420\mathrm{~km}.$ You need the radius to find the area of the circle.

\begin{aligned}r&=420\div{2} \\\\ r&=210\mathrm{~km} \end{aligned}

Use the formula $\bf{\textbf{A}=\pi \textbf{r}^2}$ to calculate the area of the circle.

\begin{aligned}A&=\pi\times{r}\times{r} \\\\ &=\pi\times{210}\times{210} \\\\ &=44100\pi \end{aligned}

Leave the answer in the form $44100\pi.$

State answer with the correct units.

44100\pi\mathrm{~km}^2

Example 5 : calculating the area of the circle given the circumference of a circle

A circle has a circumference of $21\mathrm{~cm}.$ Calculate its area. Give your answer to $2 \text { dp}.$

Find the radius of the circle.

The question gives you the circumference of the circle. You need the radius.

You know that the circumference of a circle is equal to $C=2\pi{r}.$

Step by step guide: Circumference of a circle

This means you can find the radius of the circle from the circumference, see below:

\begin{aligned}&21=2\pi{r} \\\\ &\cfrac{21}{2\pi}=\cfrac{2\pi{r}}{2\pi} \\\\ &\cfrac{21}{2\pi}=r \end{aligned}

Notice how to leave the answer in terms of $\pi$ at this stage. This is so you do not cause a rounding error later on in the question.

Use the formula $\bf{\textbf{A}=\pi \textbf{r}^2}$ to calculate the area of the circle.

\begin{aligned}A&=\pi\times{r}\times{r} \\\\ &=\pi\times\cfrac{21}{2\pi}\times\cfrac{21}{2\pi} \\\\ &=35.09366465… \\\\ &=35.09\text{ (2 dp)} \end{aligned}

State answer with the correct units.

35.09\mathrm{~cm}^2

Example 6 : finding the radius of a circle when given the area

A circle has an area of $16\pi\mathrm{~cm}^2.$ Find the length of the radius.

Find the radius of the circle.

In this question, you are being asked to find the radius of the circle. The radius is simply $r.$

Use the formula $\bf{\textbf{A}=\pi \textbf{r}^2}$ to calculate the area of the circle.

The question asks to find the radius, so you will be working backwards.

\begin{aligned}A&=\pi{r^2} \\\\ 16\pi&=\pi{r^2} \end{aligned}

Divide both sides by $\pi,$ and you are left with

$16=r^2$

Now, take the square root of each side of the equation.

\begin{aligned}\sqrt{16}&=\sqrt{r^2} \\\\ 4&=r \end{aligned}

State answer with the correct units.

The radius of the circle is $4\mathrm{~cm}^2.$

Teaching tips for area of a circle

For students struggling with the area of a circle, make sure that they have the basics down, including the parts of a circle, specifically the diameter and radius.

Students need ample opportunities to practice with the area of a circle. The use of worksheets with increased levels of difficulty is an easy way to provide this to students.

Use of technology tools, such as an area of a circle calculator or online practice opportunities is a way to engage students and provide another means of practice.

Show students real world applications of finding the area of a circle, including finding the area of a pizza or a circle tile within the school. Real-life examples provide students with context as to why the content is important to learn.

Easy mistakes to make

Not using the radius
You must have the radius to find the area of a circle from the formula.
A question may not give you the radius directly, for example it may give you the diameter. You must use the information given to find the radius of circle first.

Not including the correct unit of area
When working with area you will use square units, including square centimeters $(cm^2),$ square inches $(in^2),$ square meters $(m^2),$ etc.

Not giving answer in terms of $\bf{\pi}$
Sometimes the question may ask you to give the answer ‘in terms of $\pi$ ’. This means you do not give the numerical answer that is produced when you multiply it by $\pi.$

For example,
$6\times \pi=6\pi$ (this is an answer in terms of pi)
$6\times \pi=18.8495592…$ (this answer is not in terms of pi)

Practice area of a circle questions

6\mathrm{~cm}

3\mathrm{~cm}

12\mathrm{~cm}

6\pi\mathrm{~cm}

The diameter of the circle is twice the size of the radius. Therefore to find the radius you can divide the diameter by $2.$

6\div{2}=3\mathrm{~cm}

9.42\mathrm{~in}^2

21.39\mathrm{~in}^2

28.27\mathrm{~in}^2

19.26\mathrm{~in}^2

\begin{aligned}A&=\pi{r^2} \\\\ &=\pi\times{r}\times{r} \\\\ &=\pi\times{3}\times{3} \\\\ &=9\pi \\\\ &=28.2743… \end{aligned}

A=28.27\mathrm{~in}^2

40\pi

26\pi

158\pi

169\pi

\begin{aligned}A&=\pi{r^2} \\\\ &=\pi\times{r^2} \\\\ &=\pi\times{13^2} \\\\ &=169\pi \end{aligned}

32,400\pi

16,200\pi

129,600\pi

62,800\pi

First, calculate the radius by dividing the diameter by $2.$

360\div{2}=180\mathrm{~km}

Then, use the formula $A=\pi{r^2}$ to find the area.

\begin{aligned}A&=\pi{r^2} \\\\ &=\pi\times{r}\times{r} \\\\ &=\pi\times{180}\times{180} \\\\ &=32,400\pi \end{aligned}

45,156.25\mathrm{~km}^2

141,862.54\mathrm{~km}^2

14,862.54\mathrm{~km}^2

41,862.54\mathrm{~km}^2

First, calculate the radius by dividing the diameter by $2.$

425\div{2}=212.5\mathrm{~km}

Then, use the formula $A=\pi{r^2}$ to find the area.

\begin{aligned}A&=\pi{r^2} \\\\ &=\pi\times{r}\times{r} \\\\ &=\pi\times{212.5}\times{212.5} \\\\ &=45,156.25\pi \\\\ &=141,862.54\mathrm{~km}^2 \end{aligned}

450\mathrm{~cm}

25\mathrm{~cm}

30\mathrm{~cm}

10\mathrm{~cm}

\begin{aligned}A&=\pi{r^2} \\\\ 100\pi&=\pi{r^2} \end{aligned}

Divide both sides by $\pi,$ and you are left with

100=r^2

Now, take the square root of each side of the equation.

\begin{aligned}\sqrt{100}&=\sqrt{r^2} \\\\ 10&=r \\\\ r&=10\mathrm{~cm} \end{aligned}

Area of a circle FAQs

What is the formula for the surface area of a circle?

Surface area typically refers to 3D shapes, so you would not find the surface area of a circle, but the surface area of a sphere. The formula for finding the surface area of a sphere is $4\pi{r^2}.$

How do you find the area of a semicircle?

The area of a semicircle is half the area of a circle. You can find the area of the circle using the formula $A=\pi{r^2}$ and then divide it by $2.$ Or you can use the formula $A=\cfrac{1}{2}\times\pi{r^2}.$

The next lessons are

Sector arcs and segments
Circle theorems
Prism shape
Trigonometry

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.