[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
Solving quadratic equation
Here you will learn about solving quadratic equations and how to do it using a graph, factoring the equation or using the quadratic formula.
Students will first learn about solving quadratic equations as part of algebra in high school.
What is solving quadratic equations?
Solving quadratic equations is finding the roots or the x- intercepts of the parabola formed by a quadratic equation.
For example,
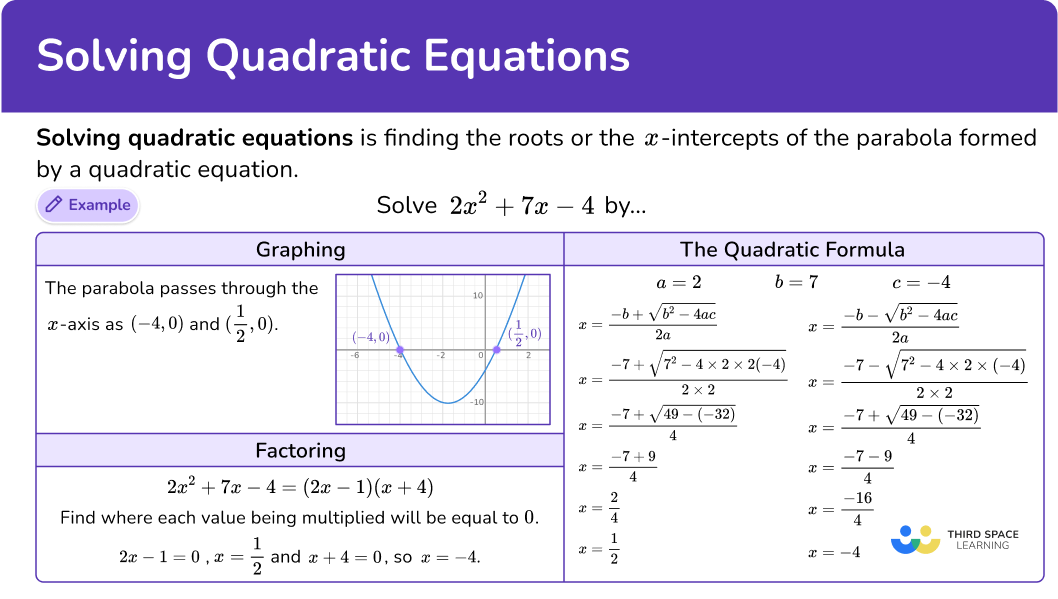
Solve 2x^2+7x-4 by using its graph below.
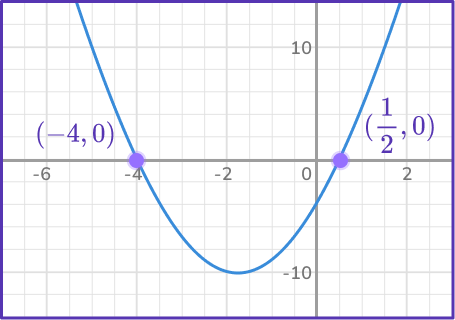
The parabola passes through the x- axis as (-4,0) and \left(\cfrac{1}{2}, 0\right).
The solutions are x=-4 and x=\cfrac{1}{2}.
For example,
Solve 2x^2+7x-4=0 by factoring.
\begin{aligned} & 2 x^2+7 x-4=0 \\\\ & (2 x-1)(x+4)=0 \end{aligned}Find where each value being multiplied will be equal to 0.
2x-1=0, so x=\cfrac{1}{2}
and
x+4=0 so x=-4
For example,
Solve 2x^2+7x-4=0 using the quadratic formula.
The quadratic formula uses the values from the constant terms a, b and c when quadratic equations are in the general form ax^2+b x+c=0.
\begin{aligned} & a=2 \\\\ & b=7 \\\\ & c=-4 \end{aligned}\begin{aligned} & x=\cfrac{-b+\sqrt{b^2-4 a c}}{2 a} \\\\ & x=\cfrac{-7+\sqrt{7^2-4 \times 2 \times(-4)}}{2 \times 2} \\\\ & x=\cfrac{-7+\sqrt{49-(-32)}}{4} \\\\ & x=\cfrac{-7+9}{4} \\\\ & x=\cfrac{2}{4} \\\\ & x=\cfrac{1}{2} \end{aligned} \quad \begin{aligned} & x=\cfrac{-b-\sqrt{b^2-4 a c}}{2 a} \\\\ & x=\cfrac{-7-\sqrt{7^2-4 \times 2 \times(-4)}}{2 \times 2} \\\\ & x=\cfrac{-7-\sqrt{49-(-32)}}{4} \\\\ & x=\cfrac{-7-9}{4} \\\\ & x=\cfrac{-16}{4} \\\\ & x=-4 \end{aligned}
What is solving quadratic equations?
Common Core State Standards
How does this relate to high school math?
- Algebra – Reasoning with Equations and Inequalities (HSA.REI.B.4b)
Solve quadratic equations in one variable. Solve quadratic equations by inspection ( e.g., for x^2=49), taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation. Recognize when the quadratic formula gives complex solutions and write them as a \pm bi for real numbers a and b.
![[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)
Use this quiz to check your grade 6 – grade 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th to 8th grade algebra topics to identify areas of strength and support!
DOWNLOAD FREE [FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)
Use this quiz to check your grade 6 – grade 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th to 8th grade algebra topics to identify areas of strength and support!
DOWNLOAD FREEHow to solve a quadratic equation by graphing
In order to solve quadratic equations by graphing:
- Graph the quadratic equation.
- Identify the \textbf{x}- intercepts.
Solving quadratic equation examples
Example 1: solve a quadratic equation by looking at its graph
Solve the following equation by using a graph: x^2-x-6.
- Graph the quadratic equation.
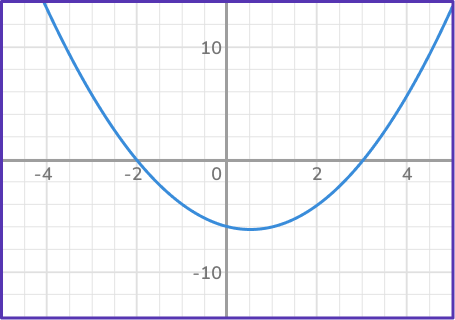
2Identify the \textbf{x}- intercepts.
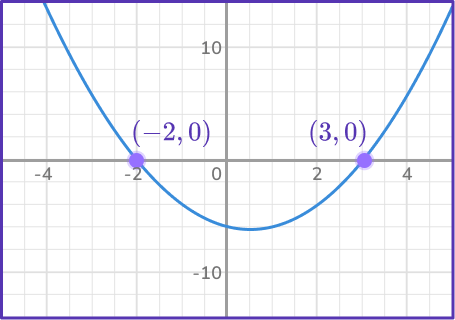
The parabola passes through the x- axis as (-2,0) and (3,0)
The solutions are x=-2 and x=3.
Example 2: solve a quadratic equation by looking at its graph
Solve the following equation by using a graph: 2x^2-3x+1.125.
Graph the quadratic equation.
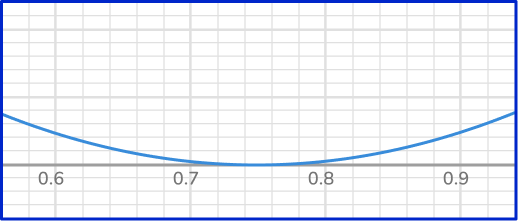
Identify the \textbf{x}- intercepts.
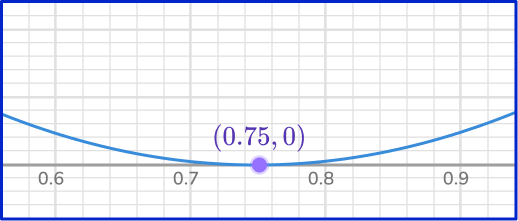
The parabola passes through the x- axis as (0.75,0). Since it crosses at the vertex of the parabola, there is only 1 solution.
The solution is x=0.75.
See also: Quadratic graphs
How to solve a quadratic equation by factoring
In order to solve quadratic equations by factoring:
- Make sure that the equation is equal to \bf{0}.
- Fully factor the quadratic equation.
- Set each expression equal to \bf{0}.
- Solve for \textbf{x}.
Example 3: solve a quadratic equation by factoring with coefficient a=1
Solve x^{2}-8x+15=0 by factoring.
Make sure that the equation is equal to \bf{0}.
Fully factor the quadratic equation
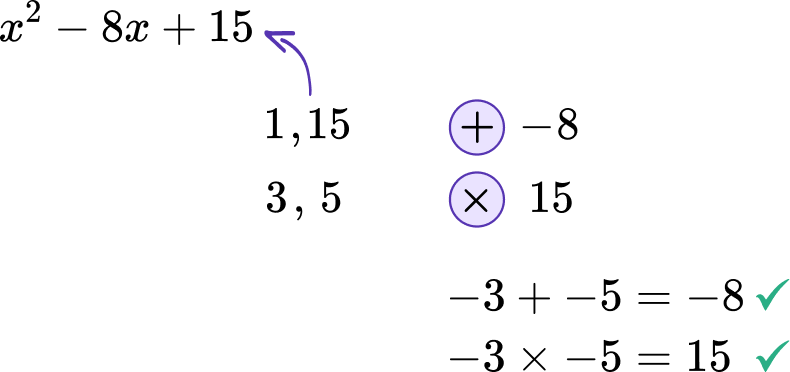
(x-3)(x-5)=0
Set each expression equal to \textbf{0}.
x-3=0 \quad x-5=0
Solve for \textbf{x}.
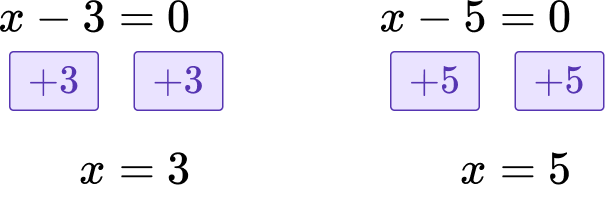
The opposite of -3 is +3, so add 3 to both sides of the equation.
The opposite of -5 is +5, so add 5 to both sides of the equation.
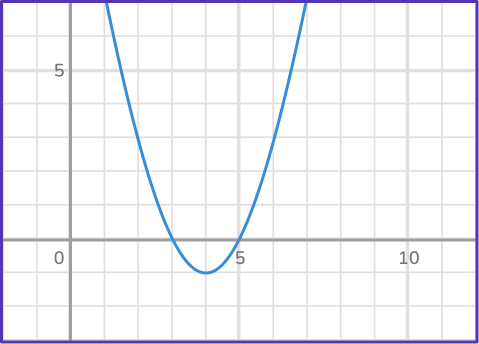
You can see the real roots of the quadratic equation are where the quadratic graph crosses the x- axis.
Example 4: solve a quadratic equation by factoring with coefficient a>1
Solve 2x^{2}+5x+3=0 by factoring.
Make sure that the equation is equal to \bf{0}.
Fully factor the quadratic equation
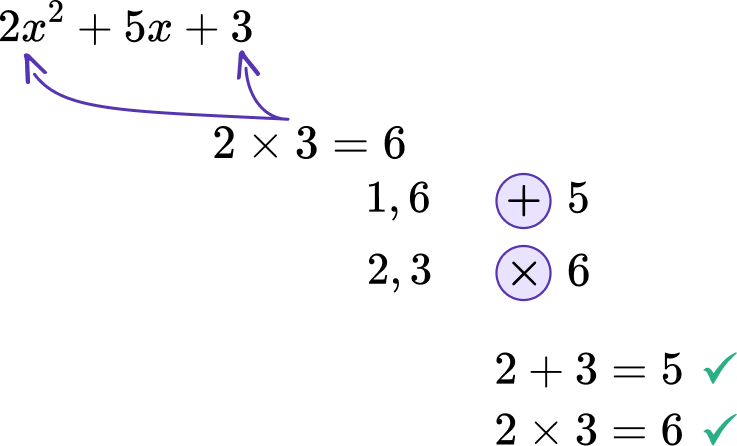
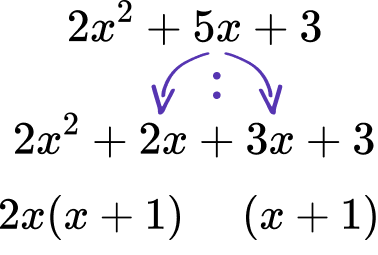
(2x+3)(x+1)=0
Set each expression equal to \textbf{0}.
2 x+3=0 \quad x+1=0
Solve for \textbf{x}.
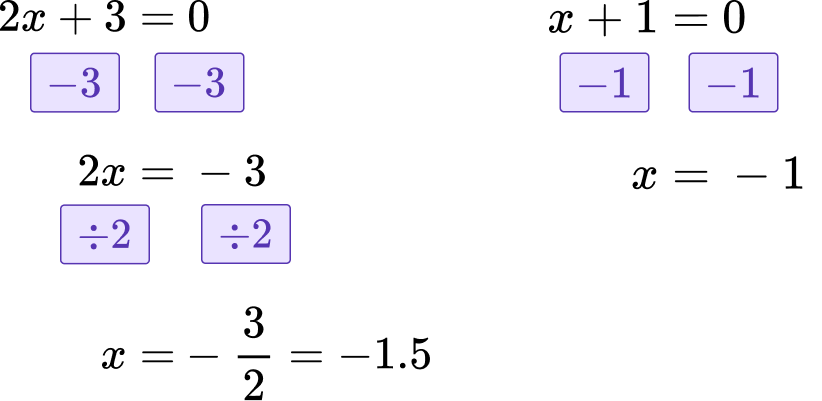
The opposite of +3 is -3, so subtract 3 to both sides of the equation.
The opposite of \times 2 is \div 2, so divide by 2 on both sides of the equation.
The opposite of +1 is -1, so -1 to both sides of the equation.
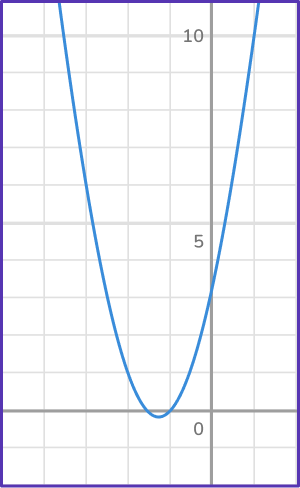
You can see the real roots of the quadratic equation are where the quadratic graph crosses the x- axis.
How to solve quadratic equations with the quadratic formula
In order to solve quadratic equations with the quadratic formula:
- Identify the value of \bf{\textbf{a}, \textbf{b}} and \textbf{c} in a quadratic equation.
- Substitute these values into the quadratic formula.
- Solve the equation with a \bf{+}, and then with a \bf{-}.
Example 5: equation of the form ax²+b x+c=0 where a = 1
Solve x^2-2 x-15=0 using the quadratic formula.
Identify the value of \bf{\textbf{a}, \textbf{b}} and \textbf{c} in a quadratic equation.
Substitute these values into the quadratic formula.
Solve the equation with a \bf{+}, and then with a \bf{-}.
\begin{aligned} & x=\cfrac{-(-2)+\sqrt{(-2)^2-4(1)(-15)}}{2(1)} \\\\ & x=\cfrac{2+\sqrt{4-(-60)}}{2} \\\\ & x=\cfrac{2+8}{2} \\\\ & x=5 \end{aligned} \quad \begin{aligned} & x=\cfrac{-(-2)-\sqrt{(-2)^2-4(1)(-15)}}{2(1)} \\\\ & x=\cfrac{2-\sqrt{4-(-60)}}{2} \\\\ & x=\cfrac{2-8}{2} \\\\ & x=-3 \end{aligned}
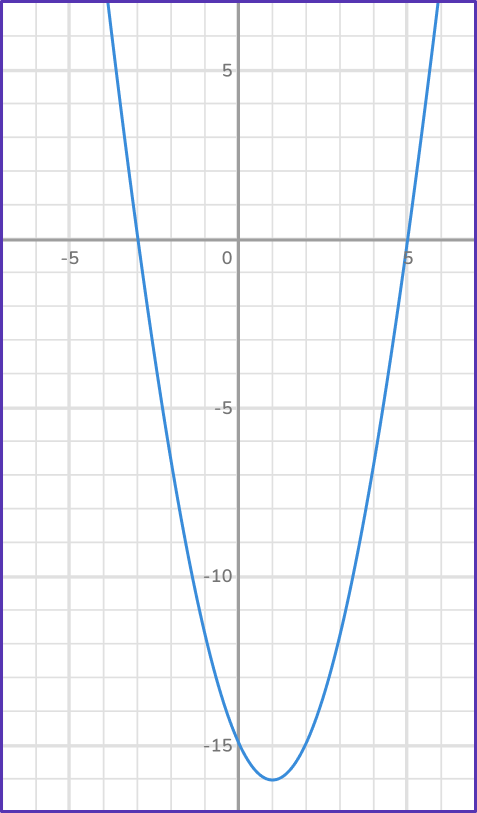
You can see the roots of the quadratic equation are where the quadratic graph crosses the x- axis.
You can also check that the solutions are correct by substituting them into the original equation.
Example 6: solutions of the quadratic equation with a<1
Solve -6 x^2+2 x-x=-2 using the quadratic formula.
Identify the value of \bf{\textbf{a}, \textbf{b}} and \textbf{c} in a quadratic equation.
First, simplify the equation so that it is in the form ax^2+b x+c=0, which leaves a quadratic expression on the left side of the equation and 0 on the right side of the equation.
-6 x^2+x=-2 \hspace{0.5cm} *Combine the like terms (2x-x)
-6 x^2+x=-2 \hspace{0.5cm} *Add 2 to both sides so that the equation equals 0
\hspace{0.8cm} +2 \hspace{0.4cm}+2
-6 x^2+x+2=0
Substitute these values into the quadratic formula.
Solve the equation with a \bf{+}, and then with a \bf{-}.
\begin{aligned} & x=\cfrac{-(1)+\sqrt{(1)^2-4(-6)(2)}}{2(-6)} \\\\ & x=\cfrac{-1+\sqrt{1-(-48)}}{-12} \\\\ & x=\cfrac{-1+7}{-12} \\\\ & x=-\cfrac{1}{2} \end{aligned} \quad \begin{aligned} & x=\cfrac{-(1)-\sqrt{(1)^2-4(-6)(2)}}{2(-6)} \\\\ & x=\cfrac{-1-\sqrt{1-(-48)}}{-12} \\\\ & x=\cfrac{-1-7}{-12} \\\\ & x=\cfrac{2}{3} \end{aligned}
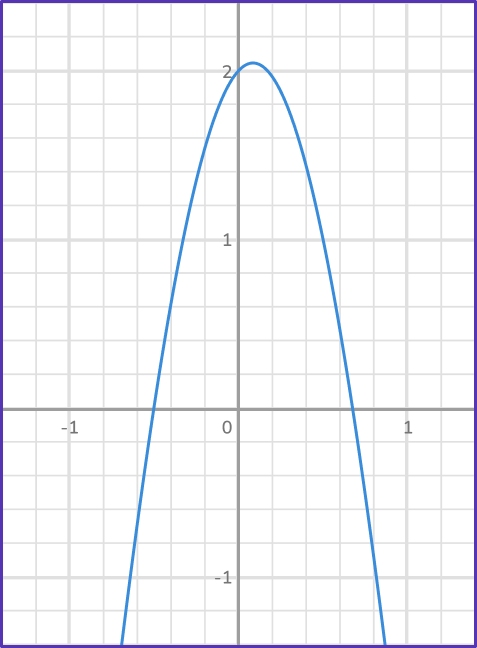
You can see the roots of the quadratic equation are where the quadratic graph crosses the x- axis.
You can also check that the solutions are correct by substituting them into the original equation.
Teaching tips for solving quadratic equations
- Let students use a graphing calculator to explore how changing the values for a, b and c in a quadratic equation changes the parabola.
- When students start using the quadratic formula, still encourage them to explain the meaning of their solutions. This way they do not forget what exactly they are solving for. One way to do this is to incorporate many real world examples of the quadratic equation that require students to explain the roots within the context of the problem.
Easy mistakes to make
- Thinking the order of the factored equation matters
When you multiply two values the order doesn’t matter.
For example,
2\times 3=3\times 2
It is the same with quadratics.
(x-6)(x+4) means (x-6)\times (x+4)
So, (x-6)(x+4)=0 is the same as (x+4)(x-6)=0.
- Forgetting to solve after factoring
Don’t forget to set the factored expression equal to zero and solve it. Always check you have answered the question.
- Thinking that an equation that does not look like \bf{\textbf{ax}^2+\textbf{b x}+\textbf{c}=0} is not quadratic
In a quadratic equation a≠ 0, but b and c can be 0.
For example,
Here is a quadratic equation that involves two square terms (perfect squares).
Notice that b = 0, because there is no term with just the variable x. However, it is still a quadratic equation and therefore can be solved.
\begin{array}{ll} \\4 x^2-16=0 & \\\\ (2 x+4)(2 x-4)=0 \end{array}
\begin{array}{ll} 2 x+4=0 \\\\ x=-2 \end{array} \quad \begin{array}{ll} 2 x-4=0 \\\\ x=2 \end{array}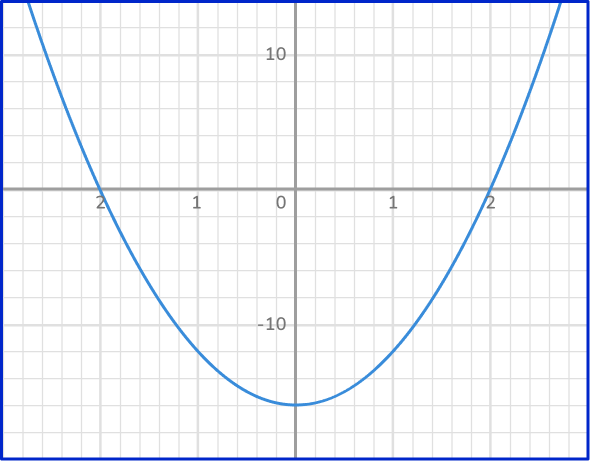
- Thinking an equation that cannot be factored has no solutions
If a quadratic equation cannot be factored, you can still solve it by using the quadratic formula. To work out the number of real solutions a quadratic equation has you can use the discriminant.
- Not converting to the form \bf{\textbf{ax}^{2}+\textbf{b x}+\textbf{c}=0} before trying to factor
While it is possible to factor a quadratic equation without it in the standard form, this can be challenging. It is recommended to use the general form shown.
Related quadratic equation lessons
- Quadratic formula
- Solving quadratic equations by graphing
- Factoring quadratic equations
Solving quadratic equations questions (by factoring)
1) Solve -x^2+2x by using its graph below.
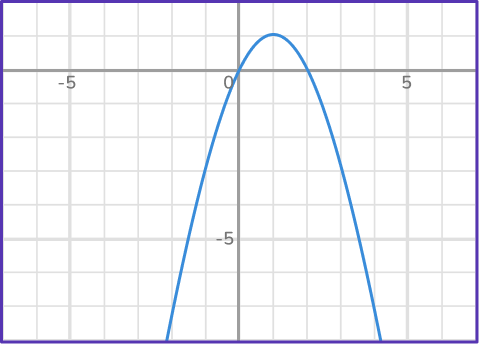
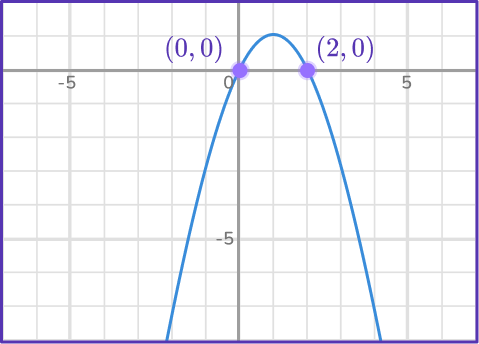
The parabola passes through the x- axis as (0,0) and (2,0).
The solutions are x = 0 and x = 2.
2) Solve x^2+10 x+9 by using its graph below.
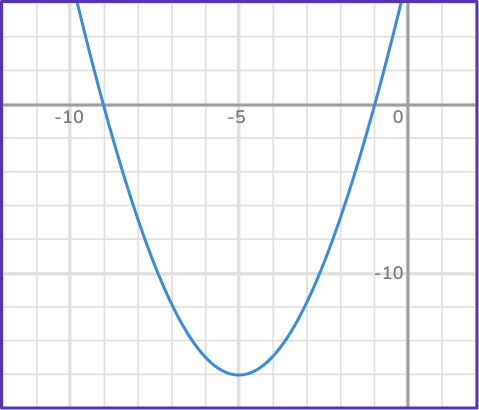
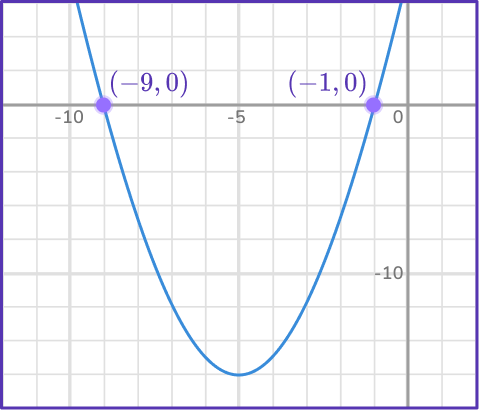
The parabola passes through the x- axis as (-1,0) and (-9,0).
The solutions are x = -1 and x = -9.
3) Solve {x}^2+5x+6=0 by factoring.
{x}^2+5x+6=0 can be factored as (x+2)(x+3).
Setting each factor equal to zero and solving leads to the solutions.
\begin{aligned} & x+2=0 \\\\ & x=-2 \end{aligned} \quad \begin{aligned} & x+3=0 \\\\ & x=-3 \end{aligned}
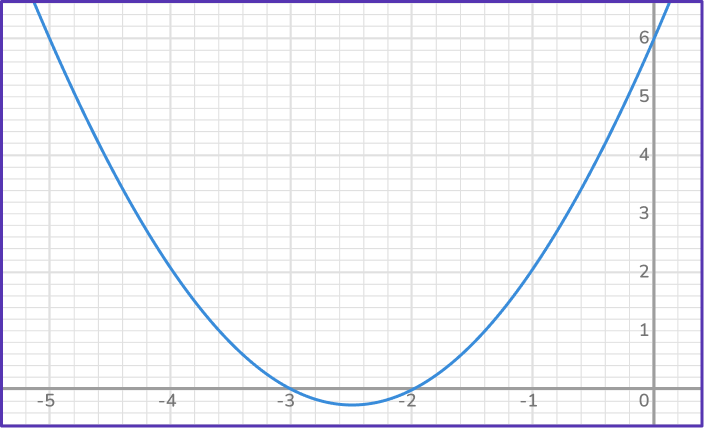
4) Solve {x}^2-x-20=0 by factoring.
x^2-x-20 can be factored as (x-5)(x+4).
Setting each factor equal to zero and solving leads to the solutions.
\begin{aligned} & x-5=0 \\\\ & x=5 \end{aligned} \quad \begin{aligned} & x+4=0 \\\\ & x=-4 \end{aligned}
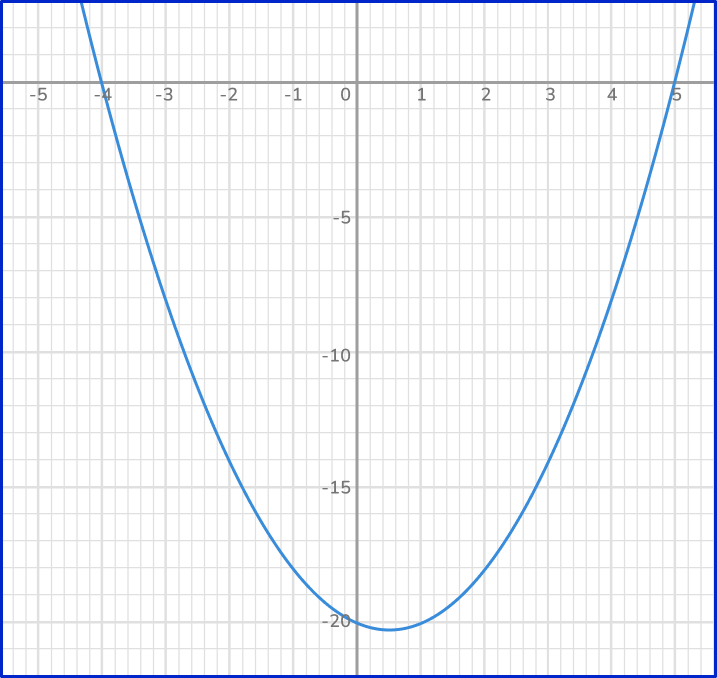
5) Solve 2{x}^2+3x-9=0 using the quadratic equation.
x=-\cfrac{3}{2}=-1.54 and x= -3
x=\cfrac{3}{2}=1.5 and x=3
x=-\cfrac{3}{2}=-1.5 and x=3
x=\cfrac{3}{2}=1.5 and x=-3
Identify a, b and c.
a=2, b=3, c=-9
Substitute these values into the quadratic formula.
\begin{aligned} & x=\cfrac{-b \pm \sqrt{b^2-4 a c}}{2 a} \\\\ & x=\cfrac{-3 \pm \sqrt{(3)^2-4(2)(-9)}}{2(2)} \end{aligned}
Solve the equation with a +, and then with a -.
\begin{aligned} & x=\cfrac{-3+\sqrt{(3)^2-4(2)(-9)}}{2(2)} \\\\ & x=\cfrac{-3+\sqrt{9-(-72)}}{4} \\\\ & x=\cfrac{-3+9}{4} \\\\ & x=\cfrac{3}{2}=1.5 \end{aligned} \quad \begin{aligned} & x=\cfrac{-3-\sqrt{(3)^2-4(2)(-9)}}{2(2)} \\\\ & x=\cfrac{-3-\sqrt{9-(-72)}}{4} \\\\ & x=\cfrac{-3-9}{4} \\\\ & x=-3 \end{aligned}
*Divide the numerator by the denominator to convert \cfrac{3}{2} to decimal form.
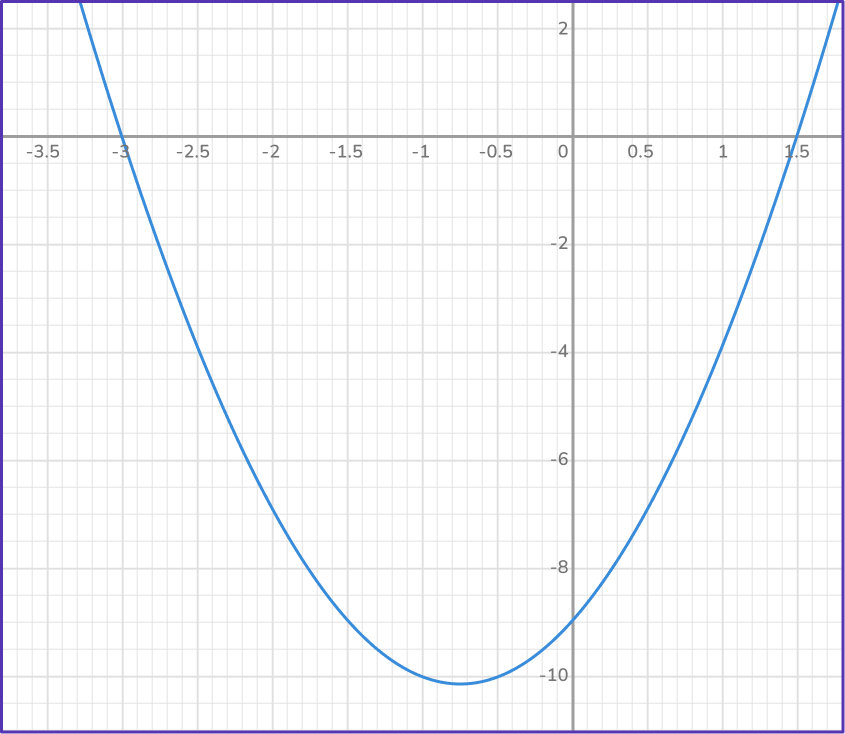
6) Solve 3{x}^2-9x+6=0 using the quadratic equation.
Identify a, b and c.
a=3, b=-9, c=6
Substitute these values into the quadratic formula.
\begin{aligned} & x=\cfrac{-b \pm \sqrt{b^2-4 a c}}{2 a} \\\\ & x=\cfrac{-(-9) \pm \sqrt{(-9)^2-4(3)(6)}}{2(3)} \end{aligned}
Solve the equation with a +, and then with a -.
\begin{aligned} & x=\cfrac{-(-9)+\sqrt{(-9)^2-4(3)(6)}}{2(3)} \\\\ & x=\cfrac{9+\sqrt{81-72}}{6} \\\\ & x=\cfrac{9+3}{6} \\\\ & x=2 \end{aligned} \quad \begin{aligned} & x=\cfrac{-(-9)-\sqrt{(-9)^2-4(3)(6)}}{2(3)} \\\\ & x=\cfrac{9-\sqrt{81-72}}{6} \\\\ & x=\cfrac{9-3}{6} \\\\ & x=1 \end{aligned}
Solving quadratic equation FAQs
It is a polynomial equation whose highest variable is to the second-degree ( exponent of 2).
The standard form is ax^2+b x+c=0 or f(x)=a x^2+b x+c. The coefficients a, b and c can be whole numbers, integers, fractions, decimals or any other real number where a ≠ 0.
It is the value below the radical in the quadratic formula. If the discriminant b^2-4ac is positive, there are two solutions. If it is 0, there is 1 solution. If it is negative, there are no real solutions.
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!