High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Combining like terms Simplifying expressions Expanding expressions Polynomial Law of exponents Simplifying fractions Multiplying and dividing fractionsFactoring the difference of two squares
Solving systems of equations by graphing Linear equationsMultiplying rational expressions
Here you will learn about multiplying rational expressions, including algebraic fractions with monomial and binomial numerators and denominators.
Students will first learn about multiplying rational expressions as part of algebra in high school.
What is multiplying rational expressions?
Multiplying rational expressions is the skill of multiplying two or more rational expressions. A rational expression is the ratio of two polynomials.
For example,
\cfrac{2a}{5}, \, \cfrac{3-gh}{4f}, or \cfrac{1}{x-x^{2}}.
To multiply them, you must combine our knowledge of multiplying fractions with your understanding of algebra.
For example,
To multiply with fractions, you multiply the numerators together, and multiply the denominators together.
This is the same for algebraic fractions, but you need to take extra care when multiplying algebraic terms or expressions.
For example,
To solve \cfrac{3 x^3}{a} \times \cfrac{5 x}{2 b}, multiply across.
\cfrac{3 x^3}{a} \times \cfrac{5 x}{2 b}=\cfrac{3 x^3 \times 5 x}{a \times 2 b}Multiply the coefficients and the variables together.
\cfrac{3 x^3 \times 5 x}{a \times 2 b}=\cfrac{(3 \times 5)\left(x^3 \cdot x\right)}{2(a \cdot b)}=\cfrac{15 x^4}{2 a b}Then simplify, if possible. In this case, the coefficients 15 and 2 have no common factors, so they cannot be simplified.
Also, the terms x^4 and 2ab have no common terms, so they cannot be simplified. The answer is in simplest terms.
\cfrac{3 x^3}{a} \times \cfrac{5 x}{2 b}=\cfrac{15 x^4}{2 a b}What is multiplying rational expressions?

Common Core State Standards
How does this relate to high school math?
- Algebra – Arithmetic with Polynomials and Rational Expressions (HS.A.APR.A.1)
Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials.
- Algebra – Arithmetic with Polynomials and Rational Expressions (HSA-APR.D.6)
Rewrite simple rational expressions in different forms; write a(x)/b(x) in the form q(x)+r(x)/b(x), where a(x), \, b(x), \, q(x), and r(x) are polynomials with the degree of r(x) less than the degree of b(x), using inspection, long division, or, for the more complicated examples, a computer algebra system.
![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Algebra Worksheet (Grade 6 to 8)
![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th and 8th grade algebra topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Algebra Worksheet (Grade 6 to 8)
![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th and 8th grade algebra topics to identify areas of strength and support!
DOWNLOAD FREEHow to multiply rational expressions
In order to multiply rational expressions:
- Multiply the numerators together and multiply the denominators together.
- Simplify the fraction if possible.
Multiply rational expressions examples
Example 1: multiplying rational expressions with monomials
Write as a single fraction in its simplest form, \cfrac{2}{a}\times\cfrac{5}{b}.
- Multiply the numerators together and multiply the denominators together.
2Simplify the fraction if possible.
The fraction \cfrac{10}{ab} cannot be simplified since the numerator and the denominator do not have any common factors.
The final answer is \cfrac{10}{ab}.
Example 2: multiplying rational expressions with a binomial in the second fraction
Write as a single fraction in its simplest form, \cfrac{4x}{5}\times\cfrac{x+7}{8}.
Multiply the numerators together and multiply the denominators together.
Note that you can leave algebraic products in factored form. However, to help with step 2 , it is best to check that they are fully factored.
The terms in the parentheses here do not share a common factor other than 1, and therefore the expression is fully factored.
Simplify the fraction if possible.
The numerator and the denominator have a common factor of 4, so divide both the numerator and the denominator by 4 to simplify the fraction.
\cfrac{4x(x+7)\div4}{40\div4}=\cfrac{x(x+7)}{10}
The final answer is \cfrac{x(x+7)}{10}.
You can expand the parentheses as another way of writing the final answer: \cfrac{x^2+7x}{10}.
Example 3: multiplying rational expressions with binomials
Write as a single fraction in its simplest form, \cfrac{5 y+6}{2} \times \cfrac{8 x}{9+x}.
Multiply the numerators together and multiply the denominators together.
Simplify the fraction if possible.
The numerator and the denominator have a common factor of 2. You can rewrite this to show the expression in both the numerator and the denominator that was multiplied by 2.
\begin{aligned}& \cfrac{2 \times[4 x(5 y+6)]}{2 \times(9+x)} \\\\
& =\cfrac{2}{2} \times \cfrac{4 x(5 y+6)}{9+x} \\\\
& =1 \times \cfrac{4 x(5 y+6)}{9+x} \\\\
& =\cfrac{4 x(5 y+6)}{9+x} \end{aligned}
Notice how the expression is rewritten to show the factors of 2 as \cfrac{2}{2}. Since \cfrac{2}{2}=1, you can simplify the expression to eliminate the common factor of 2.
The final answer is \cfrac{4 x(5 y+6)}{9+x}.
You can expand the parentheses as another way of writing the final answer: \cfrac{20 x y+24 x}{9+x}.
Example 4: multiplying rational expressions with binomials
Write as a single fraction in its simplest form, \cfrac{x+1}{12 x-4} \times \cfrac{x}{5 x}.
Multiply the numerators together and multiply the denominators together.
Note that you can leave algebraic products in factored form. However, to help with step 2 , it is best to check that they are fully factored.
In this case, the terms in the parentheses of the denominator both have a factor of 4. Therefore, write the fraction like this.
\cfrac{x(x+1)}{5 x(12 x-4)}=\cfrac{x(x+1)}{5 x \times 4(3 x-1)}=\cfrac{x(x+1)}{20 x(3 x-1)}
Simplify the fraction if possible.
The numerator and the denominator have a common factor of x, so divide both the numerator and the denominator by x to simplify the fraction.
\cfrac{x(x+1) \div x}{20 x(3 x-1) \div x}=\cfrac{x+1}{20(3 x-1)}
The final answer is \cfrac{x+1}{20(3x-1)}.
You can expand the parentheses as another way of writing the final answer: \cfrac{x+1}{60 x-20}.
Example 5: multiplying rational expressions with binomials
Write as a single fraction in its simplest form, \cfrac{3x+9}{4x}\times\cfrac{5}{2x+6}.
Multiply the numerators together and multiply the denominators together.
Note that you can leave algebraic products in factored form. However, to help with step 2 it is best to check that they are fully factored.
In this case the terms in the parentheses of the numerator both have a factor of 3, and the terms in the parentheses of the denominator both have a factor of 2. Therefore, write the fraction like this.
\cfrac{5(3x+9)}{4x(2x+6)}=\cfrac{5\times3(x+3)}{4x\times2(x+3)}=\cfrac{15(x+3)}{8x(x+3)}
Simplify the fraction if possible.
Since the numerator and the denominator share the binomial factor (x+3), it can be simplified.
\begin{aligned}& \cfrac{15(x+3)}{8 x(x+3)} \\\\
& =\cfrac{15}{8 x} \times \cfrac{x+3}{x+3} \\\\
& =\cfrac{15}{8 x} \times 1 \\\\
& =\cfrac{15}{8 x} \end{aligned}
The final answer is \cfrac{15}{8x}.
Example 6: multiplying rational expressions with binomials
Write as a single fraction in its simplest form, \cfrac{8-2y}{4 x^2} \times \cfrac{6 y+1}{5 x+6}.
Multiply the numerators together and multiply the denominators together.
When multiplying two binomials, expand the expressions fully. This will help us factor out common factors.
\cfrac{(8-2 y) \times(6 y+1)}{4 x^2 \times(5 x+6)}=\cfrac{48 y-12 y^2-2 y+8}{4 x^2(5 x+6)}=\cfrac{- \, 12 y^2+46 y+8}{4 x^2(5 x+6)}
Note that you can leave algebraic products in factored form. However, to help with step 2 it is best to check that they are fully factored.
In this case the terms in the numerator have a factor of 2. Therefore, write the fraction like this.
\cfrac{- \, 12 y^2+46 y+8}{4 x^2(5 x+6)}=\cfrac{2\left(- \, 6 y^2+23 y+4\right)}{4 x^2(5 x+6)}
Simplify the fraction if possible.
Since the numerator and the denominator share the factor 2, it can be simplified.
\begin{aligned}& \cfrac{2 \times\left(- \, 6 y^2+23 y+4\right)}{2 \times\left[2 x^2(5 x+6)\right]} \\\\
& =\cfrac{2}{2} \times \cfrac{- \, 6 y^2+23 y+4}{2 x^2(5 x+6)} \\\\
& =1 \times \cfrac{- \, 6 y^2+23 y+4}{2 x^2(5 x+6)} \\\\
& =\cfrac{- \, 6 y^2+23 y+4}{2 x^2(5 x+6)} \end{aligned}
The final answer is
\cfrac{- \, 6 y^2+23 y+4}{2 x^2(5 x+6)} or \cfrac{- \, 6 y^2+23 y+4}{10 x^3+12 x^2}.
Teaching tips for multiplying rational expressions
- Start with simpler rational expressions that have integer coefficients and constants, before moving on to more complex expressions that involve rational numbers or quadratics.
- Provide trinomials as a challenge, for students who master multiplying with monomials and binomials.
- Let struggling students use a step by step guide or a tutorial, until they are comfortable trying on their own.
Easy mistakes to make
- Cross multiplying instead of multiplying fractions
When multiplying fractions, multiply the numerators together, and multiply the denominators together. Some students can confuse this with a rule called ‘cross multiplying’ – which is not the same thing.
For example,
Incorrectly choosing to cross multiply,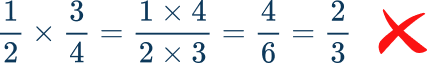
The correct solution is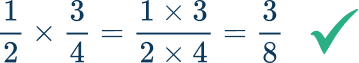
- Thinking common denominators are needed for multiplication
To add or subtract fractions you must ensure there is a common denominator. A mistake is to believe this rule also applies to the multiplication of fractions. When multiplying fractions, you can choose to write the fractions with a common denominator but this simply makes the process lengthier and it is not necessary.
For example,
Without writing the fractions with a common denominator,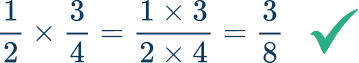
Writing the fractions with a common denominator first,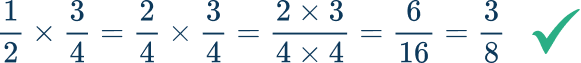
Related rational functions lessons
Practice multiplying rational expressions questions
1. Write as a single fraction in the simplest form,
\cfrac{3}{2e}\times\cfrac{8}{f}.




2. Write as a single fraction in the simplest form,
\cfrac{15}{4 x^2} \times \cfrac{3 x}{2}.




The numerator and denominator have a common factor of x.
Factor it out of both.
\begin{aligned}& =\cfrac{45 \times x}{8 x \times x} \\\\ & =\cfrac{45}{8 x} \times \cfrac{x}{x} \\\\ & =\cfrac{45}{8 x} \times 1 \\\\ & =\cfrac{45}{8 x} \end{aligned}
3. Write as a single fraction in the simplest form,
\cfrac{5+x}{12} \times \cfrac{x^2}{4}.




There are no common factors, so the expression is in simplest form.
The expression can be expanded to \cfrac{5 x^2+x^3}{48}.
4. Write as a single fraction in the simplest form,
\cfrac{2x+3}{2}\times\cfrac{2(2x+1)}{3}.




The numerator and denominator have a common factor of 2.
\begin{aligned}& =\cfrac{2\left(4 x^2+8 x+3\right)}{2(3)} \\\\ & =\cfrac{4 x^2+8 x+3}{3} \end{aligned}
5. Write as a single fraction in the simplest form,
\cfrac{4x+4}{7}\times\cfrac{3x}{2x+2}.




The parentheses in the numerator have a common factor of 4 and the parentheses in the denominator have a common factor of 2.
Factor each out of the expression.
\begin{aligned}& =\cfrac{3 x \times 4(x+1)}{7 \times 2(x+1)} \\\\ & =\cfrac{12 x(x+1)}{14(x+1)} \end{aligned}
The numerator and denominator have a common factor of 2(x + 1). Factor this out of the expression.
\begin{aligned}& =\cfrac{6 x \times 2(x+1)}{7 \times 2(x+1)} \\\\ & =\cfrac{6 x}{7} \times \cfrac{2(x+1)}{2(x+1)} \\\\ & =\cfrac{6 x}{7} \times 1 \\\\ & =\cfrac{6 x}{7} \end{aligned}
6. Write as a single fraction in the simplest form,
\cfrac{x^2-36}{4 x-8} \times \cfrac{x-6}{2}.




There are no common factors, so the expression is in simplest form.
Multiplying rational expressions FAQs
To divide with fractions, first write the reciprocal of the dividing fraction. Then multiply the numerators together and multiply the denominators together to find the quotient.
For example,
\cfrac{4b}{3} \div \cfrac{7a}{b}=\cfrac{4b}{3} \times \cfrac{b}{7a}=\cfrac{4b\times b}{3\times 7a}=\cfrac{4b^2}{21a}.
It follows the formula a^2-b^2=(a+b)(a-b), which means the difference of the square of a and b is the product of their sum and difference.
They are a fraction where the numerator, denominator or both are a fraction.
For example,
\cfrac{\cfrac{2 x}{4}}{7+x}
All rational and irrational numbers are real numbers. Complex and imaginary numbers are not real numbers.
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!