High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Fractions Algebraic expressions Factoring out theFactoring the difference of two squares
Simplifying rational expressions
Here you will learn about simplifying rational expressions (algebraic fractions), including different powers of x, quadratics, and the difference of two squares.
Students first learn how to work with rational expressions in Algebra I and expand that knowledge as they deeply explore rational functions in Algebra II.
What is simplifying rational expressions?
Simplifying rational expressions is simplifying an algebraic fraction into its lowest terms. Similar to how you simplified numerical fractions, you need to find the greatest common factor of the numerator and denominator of the rational expression to cancel out.
When you simplified a numerical fraction like, \cfrac{6}{24}, you looked for the greatest common factor of the numerator and the denominator.
To find the greatest common factor (GCF) , you can break the numerator and the denominator down into its prime factors.
\begin{aligned}& 6=2 \times 3 \\\\ & 24=2 \times 2 \times 2 \times 3 \end{aligned}The prime factors they have in common is the greatest common factor.
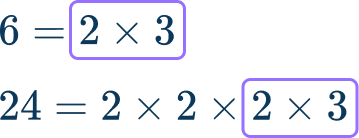
The greatest common factor is: 2\times{3}=6
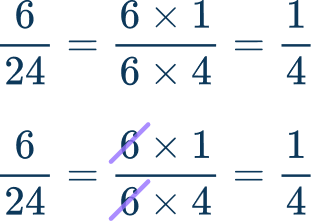
Now let’s look at a rational expression to simplify.
\cfrac{a^2 b}{a b^3}To simplify this rational expression, use the same strategy of finding the greatest common factor to cancel out of the numerator and the denominator.
To find the greatest common factor of both the numerator and denominator, break them down into prime factors.
\begin{aligned}& a^2 b=a \times a \times b \\\\ & a b^3=a \times b \times b \times b \end{aligned}The greatest common factor is the factors common to both the numerator and the denominator.
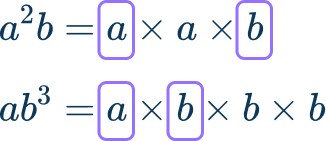
The greatest common factor of the numerator and denominator is a \times b=a b.
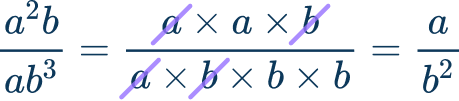
The simplified rational expression is, \cfrac{a}{b^2}.
Let’s look at another example which has quadratic expressions in the numerator and denominator of the rational expression.
\cfrac{x^2-9}{x^2+8 x+15}Before finding the greatest common factor, you have to factor.
\begin{aligned}& x^2-9=(x-3)(x+3) \\\\ & x^2+8 x+15=(x+3)(x+5) \end{aligned}To find the greatest common factor, look for the binomial factors that match to cancel out.
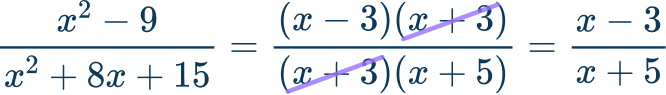
The simplified rational expression is, \cfrac{x-3}{x+5}.
What is simplifying rational expressions?

Common Core State Standards
How does this apply to high school math?
- High School Algebra: Arithmetic with Polynomials and Rational Expressions (HSA-APR.D.6)
Rewrite simple rational expressions in different forms; write \cfrac{a(x)}{b(x)} in the form q(x)+\cfrac{r(x)}{b(x)}, where a(x), \, b(x), \, q(x), and r(x) are polynomials with the degree of r(x) less than the degree of b(x), using inspection, long division, or, for the more complicated examples, a computer algebra system.
![[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)
![[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th and 8th grade algebra topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)
![[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th and 8th grade algebra topics to identify areas of strength and support!
DOWNLOAD FREEHow to simplify rational expressions
In order to simplify rational expressions:
- Break the numerator and denominator into prime factors to find the \textbf{GCF}.
- Cancel the \textbf{GCF} from the numerator and denominator.
- Write the simplified rational expression.
Simplifying rational expression examples
Example 1: algebraic fractions
Simplify the algebraic expression,
\cfrac{x^2 y^3}{x y^2} .
- Break the numerator and denominator into prime factors to find the \textbf{GCF}.
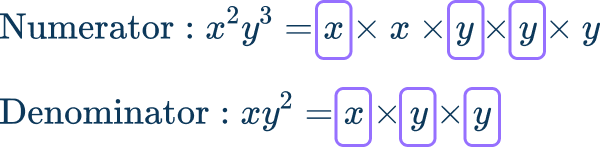
The greatest common factor is x \times y \times y=x y^2
2Cancel the \textbf{GCF} from the numerator and denominator.
\cfrac{x^2 y^3}{x y^2}=\cfrac{\cancel{x} \times x \times \cancel{y} \times \cancel{y} \times y}{\cancel{x} \times \cancel{y} \times \cancel{y}}=\frac{xy}{1}3Write the simplified rational expression.
\cfrac{x^2 y^3}{x y^2}=xyThe simplified expression is: xy
Example 2: algebraic fractions
Simplify the algebraic expression,
\cfrac{4 a b^2}{18 a^2 b^3} .
Break the numerator and denominator into prime factors.
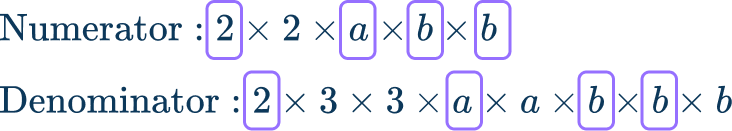
The greatest common factor is: 2 \times a \times b \times b=2 a b^2
Cancel the \textbf{GCF} from the numerator and denominator.

Write the simplified rational expression.
The simplified expression is, \cfrac{2}{9 a b} .
Example 3: factor GCF
Simplify the rational expression,
\cfrac{6x+12}{10x+20} .
Break the numerator and denominator into prime factors to find the \textbf{GCF}.
In this case, in order to break both the denominator and numerator down into prime factors, you need to apply a factoring strategy which is to factor out the GCF from the numerator and the GCF from the denominator.
\begin {aligned} &\text{Numerator}\text{:} \, 6 x+12=6(x+2) \rightarrow 2 \times 3 \times(x+2) \\\\ &\text{Denominator}\text{:} \, 10 x+20=10(x+2) \rightarrow 2 \times 5 \times(x+2) \end {aligned}
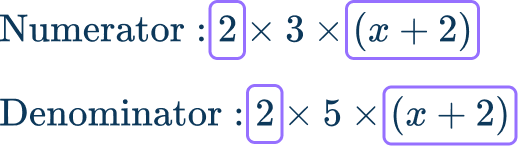
The greatest common factor is: 2 \times(x+2)=2(x+2)
Cancel the \textbf{GCF} from the numerator and denominator.
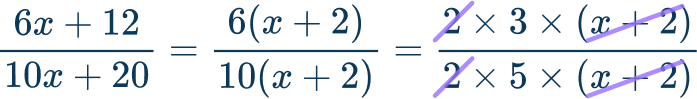
Write the simplified rational expression.
The simplified expression is, \cfrac{3}{5} .
Example 4: difference of squares
Simplify the rational expression,
\cfrac{x-4}{x^2-16} .
Break the numerator and denominator into prime factors to find the \textbf{GCF}.
In this case, you need to factor the denominator using the difference of squares. The numerator cannot be factored.
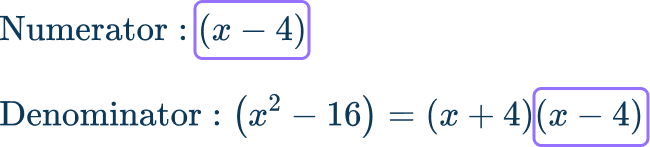
The greatest common factor is the binomial, (x-4) .
Cancel the \textbf{GCF} from the numerator and denominator.

Write the simplified rational expression.
The simplified expression is, \cfrac{1}{x+4} .
Note: The numerator is 1 because when everything cancels out, you are left with a 1.
Example 5: quadratic ÷ quadratic
Simplify the rational function,
\cfrac{x^{2}-3x-10}{x^{2}+2x-35} .
Break the numerator and denominator into prime factors to find the \textbf{GCF}.
In this case, you need to factor the trinomial in the numerator and the denominator.
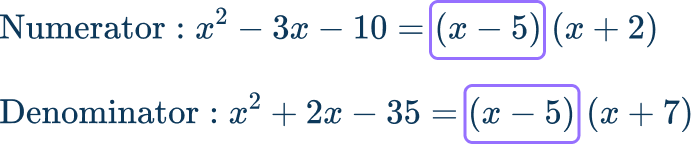
The greatest common factor is x-5 .
Cancel the \textbf{GCF} from the numerator and denominator.
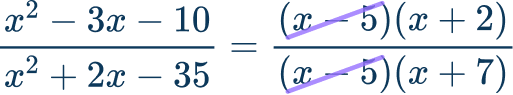
Write the simplified rational expression.
The simplified expression is \cfrac{x+2}{x+7} .
Example 6:
Simplify the rational expression,
\cfrac{x^2-36}{x^2-9 x+18} .
Break the numerator and denominator into prime factors to find the \textbf{GCF}.
In this case, factor the numerator and the denominator before finding the greatest common factor.
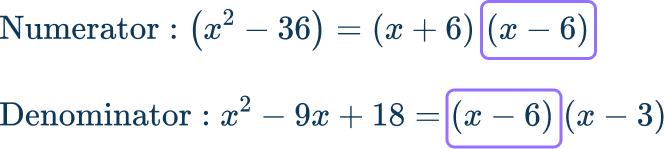
The greatest common factor is x-6 .
Cancel the \textbf{GCF} from the numerator and denominator.
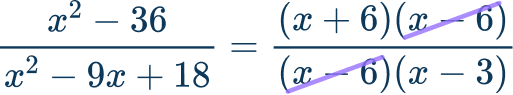
Write the simplified rational expression.
The simplified expression is, \cfrac{x+6}{x-3} .
Teaching tips for simplifying rational expressions
- Make connections between simplifying numerical fractions and simplifying rational functions so that students can make connections.
- Use active learning activities such as scavenger hunts or game playing to have students review skills instead of giving them a worksheet.
- Encourage students who are struggling to use digital platforms such as Khan Academy so they can view tutorial videos.
Easy mistakes to make
- Forgetting to factor expressions
For example when simplifying the rational expression,
\cfrac{5 x+20}{10 x+60}, cancelling out terms before factoring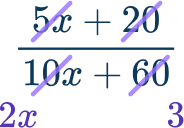
\cfrac{5 x+20}{10 x+60}≠ \cfrac{1}{2 x+3}
Instead, factor the numerator and the denominator using a factoring strategy first, then look to cancel out the greatest common factor.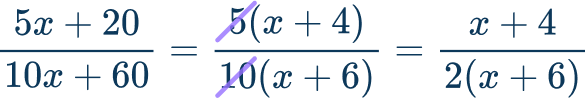
\cfrac{5 x+20}{10 x+60}=\cfrac{x+4}{2(x+6)}
- Placing a \bf{0} in the numerator or denominator when everything cancels
For example, when simplifying the rational expression \cfrac{3 x}{9 x^2}, \, 3x is the greatest common factor, \cfrac{3 x}{9 x^2}=\cfrac{3 x}{3 \times 3 \times x \times x}≠ \cfrac{0}{3 x}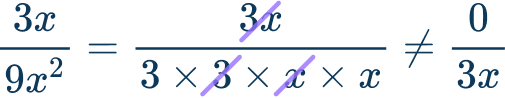
Instead, when all the terms cancel, you are left with a 1.
\cfrac{3 x}{9 x^2}=\cfrac{3 x}{3 \times 3 \times x \times x}=\cfrac{1}{3 x}
- Factoring incorrectly
For example, when factoring a binomial, thinking that you just put in parenthesis, 5 x+10≠ 5(x+10). You have to divide the factor you are factoring out by all the terms in the parenthesis, 5 x+10=5(x+2) .
Factoring a trinomial incorrectly by not being mindful of the signs. For example, when factoring x^2-10 x+24≠ (x+4)(x+6)
Be careful of the signs, and notice the - \, 10 as the coefficient of the b -term.
x^2-10 x+24=(x-4)(x-6)
For more help with factoring go to:
Step-by-step guide: Factoring
Related rational function lessons
Practice simplifying rational expressions questions
1. Simplify the rational function.
\cfrac{x^3 y}{x y^4}




Break down the numerator and the denominator into prime factors to find the greatest common factor and cancel out the greatest common factor.
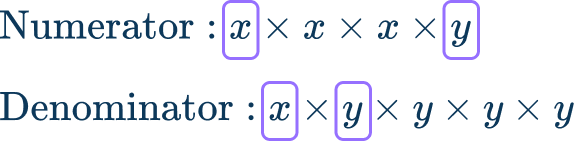
The greatest common factor is the monomial, x \times y=x y
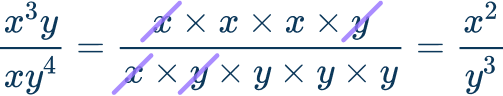
2. Write the rational expression in simplified form.
\cfrac{3 a b^3}{9 a b}




To simplify \cfrac{3 a b^3}{9 a b} , break the numerator and denominator into prime factors to identify the greatest common factor.
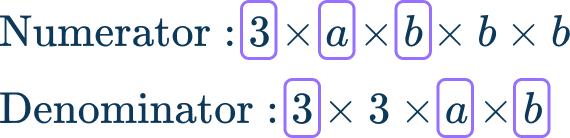
The greatest common factor is 3 \times a \times b=3 a b
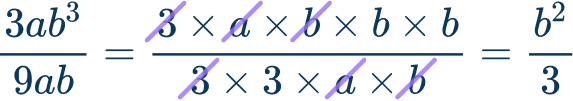
3. Simplify the rational expression.
\cfrac{10x+12}{15x+18}




To simplify the expression \cfrac{10 x+12}{15 x+18} , factor the numerator and denominator before finding the greatest common factor to cancel out.
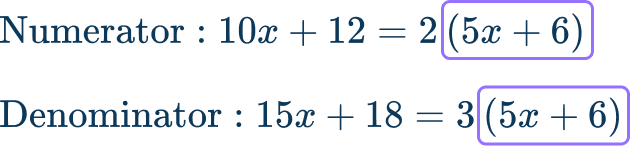
Since (5x+6) is the greatest common binomial factor, you can cancel it off the numerator and denominator.
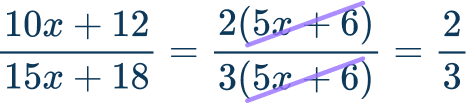
\cfrac{10x+12}{15x+18}=\cfrac{2(5x+6)}{3(5x+6)}=\cfrac{2}{3}
4. Simplify the rational expression.
\cfrac{x^{2}+2x-24}{x^{2}+x-30}




In order to simplify the rational expression, you must first factor the trinomials in both the numerator and denominator. Then, identify the common factor to cancel out.
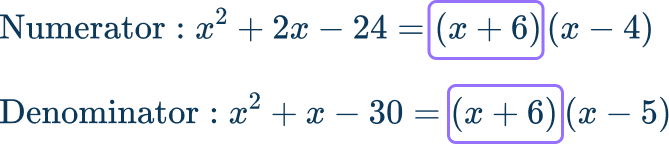
The greatest common factor is (x+6).
Rewrite the original expression in factored form.
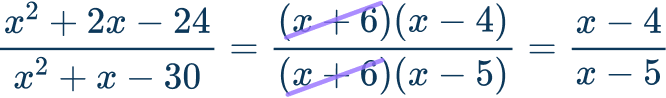
The simplified expression is \cfrac{x-4}{x-5} .
5. Simplify the rational expression, \cfrac{x^2-9 x+20}{x^2-25}




In order to simplify the expression, you need to factor both the numerator and the denominator. Then identify the common factor to cancel out.
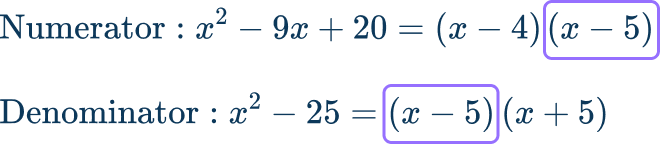
In this case, the common factor is (x-5). Now, rewrite the rational expression in factored form.
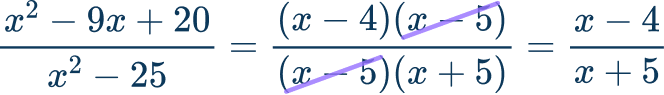
The final answer is \cfrac{x-4}{x+5} .
6. What is the rational expression in simplest form?
\cfrac{9x-27}{x^{2}+4x-21}




In order to simplify the expression, you have to factor the numerator and the denominator before finding the greatest common factor. Then identify the common factor to cancel out.
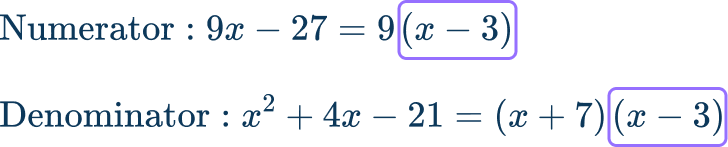
Rewrite the expression in factors and cancel out the common factors.
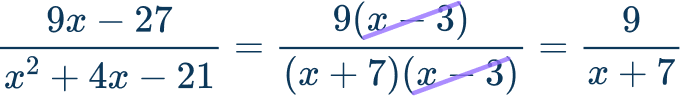
The simplified expression is \cfrac{9}{x+7} .
Simplifying rational expressions FAQs
The strategy of adding and subtracting rational functions is similar to when you add and subtract rational numbers (fractions). You need to find a common denominator and then combine like terms in the numerator.
To find the values of the variable of a rational equation, multiply the entire equation by the common denominator and then solve the equation.
Dividing rational expressions is similar to dividing fractions. Find the reciprocal of the second rational expression and multiply it to the first rational expression, writing the answer in simplest form.
The next lessons are
- Vectors
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!