Distance Formula

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Substitution

Coordinates math

Straight line graphs

Rate of change formula

Perpendicular lines Absolute value

Math resources Algebra Graphing linear equation

Distance formula

Here you will learn about the distance formula, including how to find the distance between two coordinates.

Students first learn about the distance formula in 8th grade as a part of geometry, and again in high school geometry as a part of expressing geometric properties with equations.

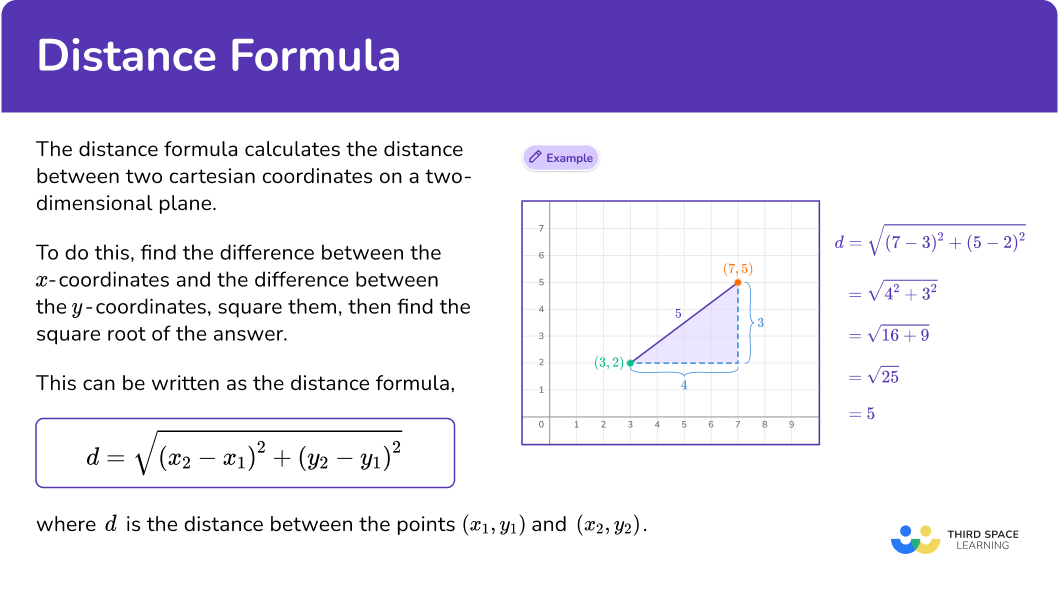
What is the distance formula?

The distance formula (also known as the Euclidean distance formula) is an application of the Pythagorean theorem $a^2+b^2=c^2$ in coordinate geometry.

It will calculate the distance between two cartesian coordinates on a two-dimensional plane, or coordinate plane.

To do this, find the differences between the $x-$ coordinates and the difference between the $y-$ coordinates, square them, then find the square root of the answer.

This can be written as the distance formula,

d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}

where $d$ is the distance between the points $\left(x_1, y_1\right)$ and $\left(x_2, y_2\right).$

For example,

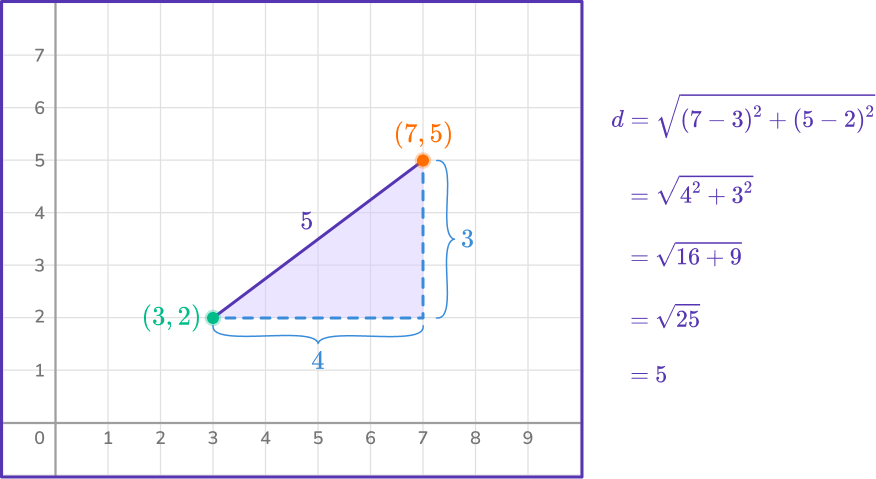
The line segment between the first point and the second point forms the hypotenuse of a right angled triangle.

The length of the hypotenuse of the right triangle is the distance between the two end points of the line segment.

What is the distance formula?

Common Core State Standards

How does this relate to $8$ th grade math?

Grade 8 – Geometry (8.G.B.8)
Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.

[FREE] Algebra Worksheet (Grade 6 to 8)

Use this quiz to check your grade 6 – grade 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th to 8th grade algebra topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Algebra Worksheet (Grade 6 to 8)

DOWNLOAD FREE

How to use the distance formula

In order to use the distance formula, you need to:

Identify the two points and label them $\bf{\left(\textbf{x}_{1}, \textbf{y}_{1}\right)}$ and $\bf{\left(\textbf{x}_{2}, \textbf{y}_{2}\right)}.$
Substitute the values into the formula, $\bf{\textbf{d}=\sqrt{\left(\textbf{x}_2-\textbf{x}_1\right)^2+\left(\textbf{y}_2-\textbf{y}_1\right)^2}}.$
Solve the equation.

Distance formula examples

Example 1: distance between two points on a coordinate axes in the first quadrant

Find the distance between the points $A$ and $B.$

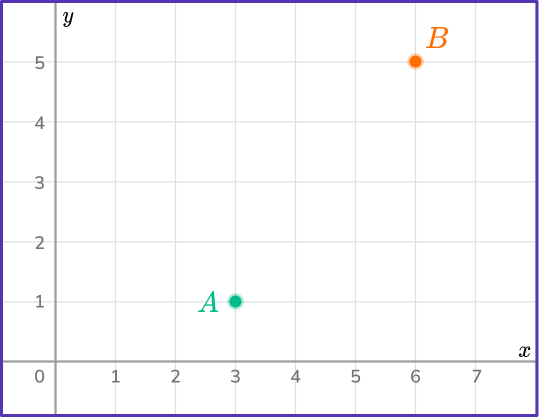
Identify the two points and label them $\bf{\left(\textbf{x}_{1}, \textbf{y}_{1}\right)}$ and $\bf{\left(\textbf{x}_{2}, \textbf{y}_{2}\right)}.$

$A=(3,1)$ and $B=(6,5).$

Let $\left(x_{1}, y_{1}\right)=(3,1)$ and $\left(x_{2}, y_{2}\right)=(6,5).$

2Substitute the values into the formula, $\bf{\textbf{d}=\sqrt{\left(\textbf{x}_2-\textbf{x}_1\right)^2+\left(\textbf{y}_2-\textbf{y}_1\right)^2}}.$

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ &=\sqrt{(6-3)^2+(5-1)^2} \end{aligned}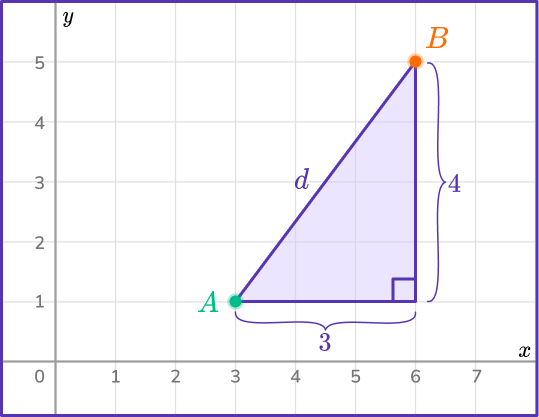

3Solve the equation.

\begin{aligned} & d=\sqrt{(6-3)^2+(5-1)^2} \\\\ & =\sqrt{3^2+4^2} \\\\ & =\sqrt{9+16} \\\\ & =\sqrt{25} \\\\ & =5 \end{aligned}

Example 2: find the distance between two points on a coordinate axes

Find the distance between the points $A$ and $B.$

Give your answer to $1$ decimal place.

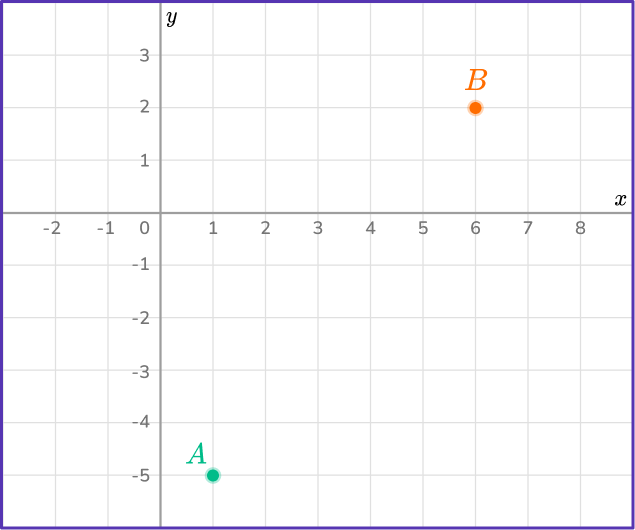
Identify the two points and label them $\bf{\left(\textbf{x}_{1}, \textbf{y}_{1}\right)}$ and $\bf{\left(\textbf{x}_{2}, \textbf{y}_{2}\right)}.$

$A=(1,-5)$ and $B=(6,2).$

Let $\left(x_{1}, y_{1}\right)=(1,-5)$ and $\left(x_{2}, y_{2}\right)=(6,2).$

Substitute the values into the formula, $\bf{\textbf{d}=\sqrt{\left(\textbf{x}_2-\textbf{x}_1\right)^2+\left(\textbf{y}_2-\textbf{y}_1\right)^2}}.$

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\\\\ &=\sqrt{(6-1)^2+(2-(-5))^2} \end{aligned}

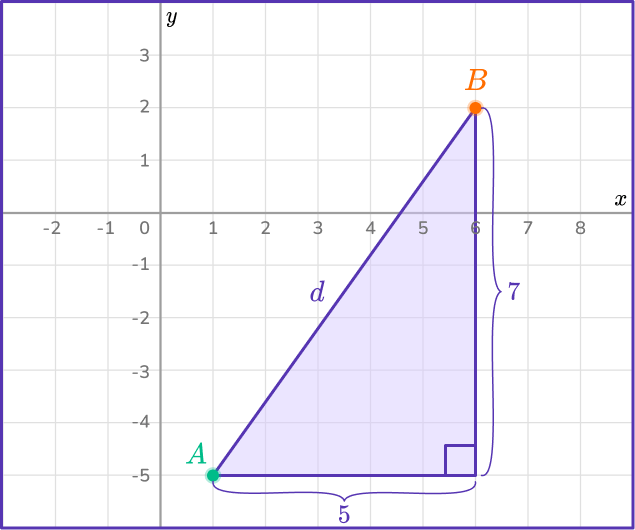
Solve the equation.

\begin{aligned} d&=\sqrt{(6-1)^2+(2-(-5))^2} \\\\ &=\sqrt{5^2+7^2} \\\\ &=\sqrt{25+49} \\\\ &=\sqrt{74} \\\\ &=8.6 \text { (1dp)} \end{aligned}

Example 3: find the distance between two given points with positive coordinates

Find the distance between the points $(1,4)$ and $(7,12).$

Identify the two points and label them $\bf{\left(\textbf{x}_{1}, \textbf{y}_{1}\right)}$ and $\bf{\left(\textbf{x}_{2}, \textbf{y}_{2}\right)}.$

Let $\left(x_{1}, y_{1}\right)=(1,4)$ and $\left(x_{2}, y_{2}\right)=(7,12).$

Substitute the values into the formula, $\bf{\textbf{d}=\sqrt{\left(\textbf{x}_2-\textbf{x}_1\right)^2+\left(\textbf{y}_2-\textbf{y}_1\right)^2}}.$

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\\\\ &=\sqrt{(7-1)^2+(12-4)^2} \end{aligned}

Solve the equation.

\begin{aligned} d&=\sqrt{(7-1)^2+(12-4)^2} \\\\ &=\sqrt{6^2+8^2} \\\\ &=\sqrt{36+64} \\\\ &=\sqrt{100} \\\\ &=10 \end{aligned}

Example 4: find the distance between any two given points

Find the distance between the points $(-2,5)$ and $(6,-7).$

Give your answer to $1$ decimal place.

Identify the two points and label them $\bf{\left(\textbf{x}_{1}, \textbf{y}_{1}\right)}$ and $\bf{\left(\textbf{x}_{2}, \textbf{y}_{2}\right)}.$

Let $\left(x_{1}, y_{1}\right)=(-2,5)$ and $\left(x_{2}, y_{2}\right)=(6,-7).$

Substitute the values into the formula, $\bf{\textbf{d}=\sqrt{\left(\textbf{x}_2-\textbf{x}_1\right)^2+\left(\textbf{y}_2-\textbf{y}_1\right)^2}}.$

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\\\\ &=\sqrt{(6-(-2))^2+(-7-5)^2} \end{aligned}

Solve the equation.

\begin{aligned} d&=\sqrt{(6-(-2))^2+(-7-5)^2}\\\\ &=\sqrt{8^2+(-12)^2} \\\\ &=\sqrt{64+144} \\\\ &=\sqrt{208} \\\\ &=14.4 \text { (1dp)} \end{aligned}

Example 5: finding a missing value given the distance

The distance between the points $(1,5)$ and $(16,k)$ is $17.$

Find the value of $k,$ where $k$ is negative.

Identify the two points and label them $\bf{\left(\textbf{x}_{1}, \textbf{y}_{1}\right)}$ and $\bf{\left(\textbf{x}_{2}, \textbf{y}_{2}\right)}.$

Let $\left(x_{1}, y_{1}\right)=(1,5)$ and $\left(x_{2}, y_{2}\right)=(16,k).$

It is also stated that $d=17.$

Substitute the values into the formula, $\bf{\textbf{d}=\sqrt{\left(\textbf{x}_2-\textbf{x}_1\right)^2+\left(\textbf{y}_2-\textbf{y}_1\right)^2}}.$

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\\\\ 17&=\sqrt{(16-1)^2+(k-5)^2} \end{aligned}

Solve the equation.

\begin{aligned} 17&=\sqrt{(16-1)^{2}+(k-5)^{2}}\\\\ 17&=\sqrt{15^{2}+(k-5)^{2}}\\\\ 289&=225+(k-5)^{2}\\\\ 64&=(k-5)^{2}\\\\ \pm8&=k-5\\\\ k&=\pm8+5\\\\ k&=13\text{ or }k=-3\\\\ \end{aligned}

The question states that $k$ is negative so $k=-3.$

Example 6: finding a missing value given the distance

The distance between the points $(2,9)$ and $(f,10)$ is $15.$

Find the value of $f,$ where $f$ is positive.

Identify the two points and label them $\bf{\left(\textbf{x}_{1}, \textbf{y}_{1}\right)}$ and $\bf{\left(\textbf{x}_{2}, \textbf{y}_{2}\right)}.$

Let $\left(x_{1}, y_{1}\right)=(2,9)$ and $\left(x_{2}, y_{2}\right)=(f, 10).$

It is also stated that $d=15.$

Substitute the values into the formula, $\bf{\textbf{d}=\sqrt{\left(\textbf{x}_2-\textbf{x}_1\right)^2+\left(\textbf{y}_2-\textbf{y}_1\right)^2}}.$

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\\\\ 15&=\sqrt{(f-2)^2+(10-9)^2} \end{aligned}

Solve the equation.

\begin{aligned} 15&=\sqrt{(f-2)^2+(10-9)^2} \\\\ 15&=\sqrt{(f-2)^2+1^2} \\\\ 225&=1+(f-2)^2 \\\\ 224&=(f-2)^2 \\\\ \pm14.9666\ldots&=f-2 \\\\ f&= \pm14.9666\ldots+2 \\\\ f&=17.0 \text { (1dp) or } f=-13.0 \text{ (1dp)} \end{aligned}

The question states that $f$ is positive so $f=17.0 (1dp).$

Teaching tips for distance formula

Use visual aids such as coordinate planes that highlight the $x-$ axis and $y-$ axis, graphs, or geometric shapes to visually represent the distance formula.

Introduce real-world scenarios where distance calculations are essential. For example, discuss scenarios involving mapping or measuring distances between points in various contexts to allow students to see the relevance of the concept.

Allow students to explore the distance formula through hands-on activities such as measuring distances on a coordinate plane or calculating distances between objects in the classroom.

Easy mistakes to make

Confusing the distance formula with the midpoint formula
An easy mistake to make is to find the midpoint instead of the distance.
The midpoint formula is $\left(\cfrac{x_{1}+x_{2}}{2}, \cfrac{y_{1}+y_{2}}{2}\right).$

Squaring negative numbers to give a negative
When using the distance formula, it is common to get negative values after the subtraction step. These values will be squared, so it is important to remember that the square of a negative value is positive.
For example, $(-3)^2=9.$

Subtracting in the wrong order
When subtracting, a common misconception is to switch the order of subtraction when plugging in the coordinates $($ for example, using $\left(x_{2}-x_{1}\right)$ and $\left(y_{1}-y_{2}\right).$
Ensure that the subtraction is done in the same order for both coordinate values: $\left(x_{2}-x_{1}\right)$ and $\left(y_{2}-y_{1}\right).$

Forgetting to simplify
When solving, neglecting to simplify the expression inside the square root is a common mistake. After squaring each term, simplify the expression inside the square root before taking the square root.

Practice distance formula questions

14

10

3.74

100

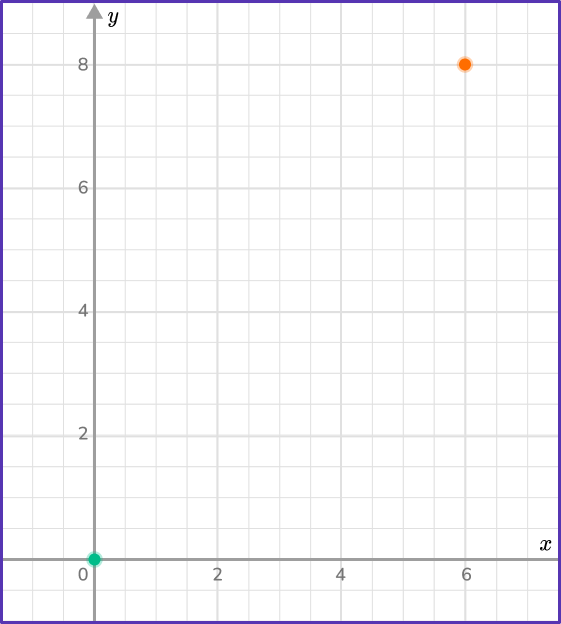
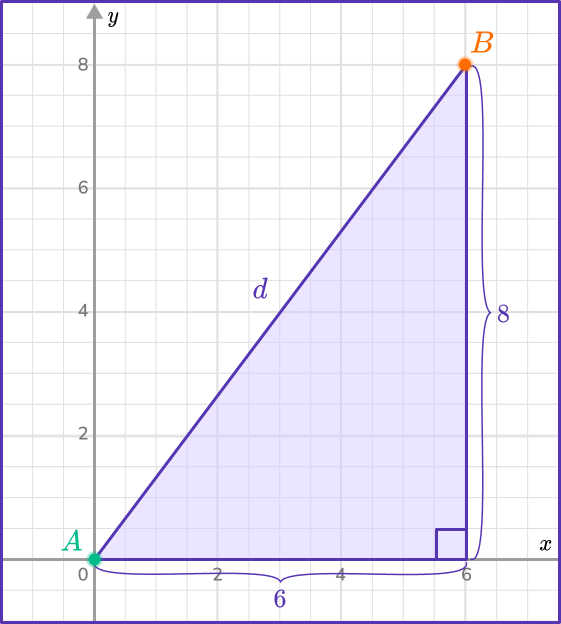
The origin is $(0,0)$ so let $(x_{1},y_{1})=(0,0)$ and $(x_{2},y_{2})=(6,8).$

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ & =\sqrt{(6-0)^2+(8-0)^2} \\\\ & =\sqrt{6^2+8^2} \\\\ & =\sqrt{36+64} \\\\ & =\sqrt{100} \\\\ & =10 \end{aligned}

Distance Formula 7 US

34

5.83

26

14

Let $\left(x_{1},y_{1}\right)=(0,10)$ and $\left(x_{2},y_{2}\right)=(24,0).$

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ & =\sqrt{(24-0)^2+(0-10)^2} \\\\ & =\sqrt{24^2+(-10)^2} \\\\ & =\sqrt{576+100} \\\\ & =\sqrt{676} \\\\ & =26 \end{aligned}

11.5

130

23.0

11.4

Let $\left(x_{1},y_{1}\right)=(5,3)$ and $\left(x_{2},y_{2}\right)=(14,10).$

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ & =\sqrt{(14-5)^2+(10-3)^2} \\\\ & =\sqrt{9^2+7^2} \\\\ & =\sqrt{81+49} \\\\ & =\sqrt{130} \\\\ & =11.4 \text { (1dp)} \end{aligned}

14.3

19

16.4

7.8

Let $\left(x_{1},y_{1}\right)=(-2,4)$ and $\left(x_{2},y_{2}\right)=(-8,-9).$

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ & =\sqrt{(-8-(-2))^2+(-9-4)^2} \\\\ & =\sqrt{(-6)^2+(-13)^2} \\\\ & =\sqrt{36+169} \\\\ & =\sqrt{205} \\\\ & =14.3 \text { (1dp)} \end{aligned}

-27

21

27

-21

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ 25&=\sqrt{(15-8)^2+(a-(-3))^2} \\\\ 25&=\sqrt{7^2+(a+3)^2} \\\\ 625&=49+(a+3)^2 \\\\ 576&=(a+3)^2 \\\\ \pm 24&=a+3 \\\\ a&=\pm 24-3\\\\ a&=21 \text { or } a=-27 \end{aligned}

As $a$ is positive, $a=21.$

3

-15

-3

15

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ 15&=\sqrt{(6-b)^2+(-8-4)^2} \\\\ 15&=\sqrt{(6-b)^2+(-12)^2} \\\\ 225&=(6-b)^2+144 \\\\ 81&=(6-b)^2 \\\\ \pm 9&=6-b \\\\ -b&=\pm 9-6\\\\ -b&=3 \text { or }-b=-15 \\\\ b&=-3 \text { or } b=15 \end{aligned}

As $b$ is negative, $b=-3.$

Distance formula FAQs

How do I use the distance formula to find the distance between two points?

The distance formula calculates the distance between two points by treating the vertical and horizontal distances as sides of a right triangle, and then finding the length of the line (hypotenuse of a right triangle) using the Pythagorean Theorem.

What is the Pythagorean Theorem?

The theorem is named after the ancient Greek mathematician, Pythagoras, and describes the relationships between the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the two other sides.

Can the distance formula be extended to a three dimensional space?

Yes, the distance formula can be extended to three dimensions. To find the distance between the two points $\left(x_{1},y_{1},z_{1}\right)$ and $\left(x_{2},y_{2},z_{2}\right)$ and using the following formula: $d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}$

The next lessons are

Geometry
Angles
Angles in parallel lines
Angles in polygons
Rate of change
Systems of equations
Number patterns

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.