8th Grade Math Games: Fun, Free Math Activities For Your Grade 8 Students (No Screens Required!)

8th grade math games and math activities are a useful tool to ensure valuable math practice whilst keeping students engaged in math class. In their last year of middle school, 8th graders face increasingly challenging classes as they prepare for the transition into high school. Eighth grade math games can bring some lightness to the math classroom. 

During eighth grade, students continue to build upon the key skills from 6th grade and 7th grade. One of the other key procedures and formulae they investigate is Pythagoras’ theorem. The games in this section will build a pupil’s understanding of Pythagoras’ theorem and enable them to practise other skills learnt during their time in middle school math.

When to use eighth grade math games

Fun math games and math problems are a useful thing for any math teacher to have up their sleeve. When a class is losing focus a fun math game can help to shake things up compared to just assigning math worksheets. Math games can also be a great way to start a lesson and end a lesson. 

Letting students get on with a math game can also allow teachers the time to walk around the classroom and observe each student to see how they are understanding the concepts. 

See also:

• 3rd grade math games
• 4th grade math games
• 5th grade math games
• 6th grade math games
• 7th grade math games

How to use these 8th grade math games

The math games below are designed to be versatile and allow for adaptations to different topics and different levels of ability so feel free to adapt the games to the needs of your class. 

All games are also quite simple and require few resources. We hope that these math resources are enjoyed by your students.

Number game: how many steps?

This game encourages students to look at multiple steps they can use to get from one number to another number. It also encourages the use of inverse operations/checking of calculations to check whether answers are correct – one of the most valuable math skills they’ll learn! 

What you need to play:

• One or more players
• Scorecard 
• Pen and paper

How to play:

• Each player is given the same starting number and answer to use (e.g. starting number of 6, answer of 17).
• Each player has 1 minute to write down the steps they would take to get from 6 to 17.
• Players can use any numbers they wish.
• Players are allowed to repeat an operation to get to an answer (e.g. for getting from 6 to 17, players can just do 6 +1, +1, +1 etc. until they get to 17), but will only score 1 point for each different operation.
• The number of different steps used is the score (e.g. 5 different steps = 5 points).
• E.g. to get from 6 to 17 in the time given: 6 (x3) = 18 (+9) = 27 (+8) = 35 (/5) = 7 (+10) = 17. This would score 5 points.
• Each player scores their number of different steps taken for each round.
• The player with the most points after the number of rounds played is the winner.
• Players are encouraged to check each other’s answers and the steps taken.
• If any stage is incorrect, the player scores 0 points for that round.

Number game: take five

This is a number game to encourage students to think carefully about strategies needed to get an answer within a range of totals. The more individual numbers used to get an answer, the more points the player gets. Students need to decide whether a strategy of getting maximum points for each answer or using fewer numbers to get each answer is the best method.

What you need to play:

• One or more players
• Pen and paper
• Playing cards can be used to generate numbers to be used by player(s) in the game

How to play:

• 5 numbers are selected at random.
• A consecutive set of 10 answers is agreed to work towards (e.g. 21-30, 41-50).
• Players are given a 5-minute time limit to get the answers to as many of the totals as possible.
• Players cannot repeat the use of a number for a single answer (unless it is part of the ones they have).
• The more individual numbers used for an answer, the more points can be awarded.
• E.g. the selected numbers are 9 5 2 7 1 and consecutive totals are from 21-30.
• For 23, the player could get to it using the following calculations: (7 x 5) = 35, (9 + 2 + 1) = 12, 35 – 12 = 23. Because 5 different numbers were used, the score is 5 points.
• For 28, the player could get to it using the following calculations: (5 – 1) = 4, 4 x 7 = 28. Because 3 different numbers have been used, the score is 3 points.
• If a player has two of the same answer (eg: two methods for getting 23), whichever one used more of their numbers is the points they score.

Fractions game: countdown

This is a more challenging version of the standard, whole number game of countdown and requires players to carry out the 4 operations using fractions and whole numbers. To make it more challenging, you can also include decimal cards. 

To make this game easier, consider giving students a number line. 

What you will need to play:

• 2 or more players
• Whole number cards (see printable resource pack)
• Fraction cards (see printable resource pack)
• 10-sided dice or 1-10 digit cards
• Paper and pen

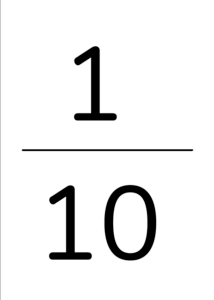
How to play:

• Place the whole number and fraction cards into 2 piles.
• Players take it in turns to select a card from the whole number or the fraction card pile.
• Once 6 cards have been selected, place them face-up on the table.
• A target number then needs to be generated (either using a 10-sided dice or 1-10 digit cards to generate the numerator and denominator).
• Players have 2 minutes to try and reach the target number using any of the 6 fraction/whole number cards and any of the 4 operations.
• The winner is the first to reach the target number or the player who is closest after 2 minutes.

PEDMAS game: 4 in a row

This is a great game for practising the rules of PEDMAS alongside strategy skills. It can be played individually or against other players.

What you will need to play:

• 1 or more players
• 4 dice
• Number grid 1-50
• 2 coloured pens

How to play:

• The first player throws the 4 dice to generate 4 numbers. 
• Using PEDMAS, they write a number sentence and colour in the square on the 1-50 grid, which contains the answer.
• The next player does the same.
• The aim of the game is to be the first player to colour in 4 squares in a row. 

Number game: nifty fifty

This game is good for developing logical thinking and problem solving.

What you need to play:

• 2 players
• Set of playing cards – Ace to 10 (Ace is worth 1)

How to play:

• Both players select 4 playing cards.
• With the 4 cards, they have 2 minutes to make a 2-digit + 2-digit number sentence which is closest to 50.
• The number sentence closest to 50 scores 1 point. If the player creates a calculation with exactly 50 as the answer, they earn 2 points.
• The winner is the player with the most points after 5 rounds.
• To add further complexity to this game, you could give each player 6 cards and then add a ‘wild’ negative number card into the game which both players have to use in their round. 

Subtraction game: sub-zero

This is a simple mental subtraction game, which doesn’t require any resources. An easy interactive game to play when there are a spare few minutes.

What you will need to play:

• 2 players

How to play:

• Starting with the number 123, the first player chooses an amount to subtract.
• The number subtracted must contain one digit from the previous answer.
• The player could choose to subtract 22, so the new number would be 101.
• A zero cannot be subtracted, so the next number has to contain a 1. 
• The next player could subtract 11, so the new number is 90.
• The only number that can be subtracted now is 9.
• The game continues. The first player to get to zero is the winner. 
• The game can be played with a different starting number each time.

Number game: countdown

This mental math game is popular for any age. Younger children can access it on a more basic level, whereas older children can use more complex multi step equations. It works well in small groups, or as a whole class activity, and encourages players to think deeply to identify calculations that will get them to the target number.

What you will need to play:

• 2 or more players
• 4 ‘large number’ cards – 25, 50, 75, 100
• 2 sets of 1-10 cards 

How to play:

• Set out the large number cards face down in one pile and the small number cards face down in another pile.
• Players take it in turns to choose a card from either the small or the large number piles and place it face down on the table.
• Once there are 6 cards face-up on the table, the target number needs to be generated.
• The target number can be generated by picking 3 number cards from a pile of 0-9 cards.
• Once the number has been generated, children have 2 minutes to try and reach that total using the 6 cards selected.
• Children can use any calculation using the 6 numbers, but each number can only be used once.
• The winner is the first person to reach the target number or the person to have the closest answer after 2 minutes.

Number game: target 24

This game is a great problem solving and ‘low floor, high ceiling game’, as players search for a solution. They can use only the basic calculations to reach the target number, or they can utilise much more complex mathematical calculations.

What you will need to play:

• A pack of cards (number cards only)
• 2 or more players

How to play:

• Shuffle the pack of cards and lay face down on the table.
• Each player picks a card and turns it face-up on the table until there are 4 cards displayed.
• The aim of the game is to make ‘24’ using only the cards on the table and any of the 4 operations.
• For example, if they have a 6, 10, 2 and 6, the solution could be very simple, such as basic addition i.e. 6 + 10 + 2 + 6 = 24.
• Older children may include more complex operations involving brackets, for example, they may have 9, 5, 6 and 9 and solve it by 5 – (9 ÷ 9) x 6 = 24.
• If nobody is able to reach 24, the player who is the closest wins.

Number game: wild jack

This is another great game for practising mental maths and numeracy skills using all four operations.

What you need to play:

• 2 or more players
• Playing cards with all picture cards (other than the Jacks removed)

How to play:

• In this game, the 1-10 cards represent their numbers, and the Jacks can represent any number from 1-10.
• The aim of the game is to reach the target number. To make the target number, shuffle the pack and turn over the top 2 cards. If either is a 10 or Jack, put them to the bottom.
• The 2 cards turned over make the target number. For example, if you turn over a 6 of spades and a 4 of hearts, your target number will be 64.
• Each player is dealt 5 cards, which are set out face up. Players can then add, subtract, multiply and divide to try to reach the target number. 
• If a target number is reached using all 5 cards, 10 points are scored. If 4 cards are used, 8 points are scored. If 3 cards are used, 6 points are scored, and so on.
• The winner is the player with the most points at the end of the game.

Number game: game of six

This is a number game to encourage children to think carefully about strategies needed to get an answer within a range of totals. The more individual numbers used to get an answer, the more points the player gets. Children need to decide whether a strategy of getting maximum points for each answer or using fewer numbers to get each answer is the best method.

What you need to play:

• One or more players
• Pen and paper
• Playing cards can be used to generate numbers to be used by player(s) in the game

How to play:

• 6 numbers are selected at random.
• A consecutive set of 10 answers is agreed to work towards (e.g. 21-30, 41-50).
• Players are given a 5-minute time limit to get the answers to as many of the totals as possible.
• Players cannot repeat the use of a number for a single answer (unless it is part of the ones they have).
• The more individual numbers used for an answer, the more points can be awarded.
• E.g. the example numbers given are: 4 8 6 3 5 9 and consecutive totals are from 31-40.
• For 31, the player could carry out the following calculations: (4 x 8) = 32, (6 – 5) = 1, 32 – 1 = 31. Because 4 different numbers were used, the score is 4 points.
• For 37, the player could carry out the following calculations: (4 x 9) = 36, (8 + 3) = 11, (6 + 5) = 11, 36 + (11 / 11) = 37. Because 6 different numbers were used, the score is 6 points.
• If a player has two of the same answer (e.g. two methods for getting 31), whichever one used more of their numbers is the points they score.

Number game: 5 of a kind

This problem-solving game is quite a challenging math activity. It requires players to think deeply about the calculations they use and how they can use quite complex calculations to achieve solutions.

What you will need to play:

• 2 or more players
• A set of cards numbered 2-9

How to play:

• Shuffle the number cards and place them face down on the table.
• The first player picks one of the cards. 
• This is their ‘5 of a kind’ number. For example, if they selected a 6, they would have 6, 6, 6, 6 and 6 to use.
• The aim of the game is to use one or more of the 5 digits to get an answer between one and ten.
• If for example, the player chose a 7, they would then need to use one or more of the digits to make the answer 1, 2, 3 up to 10. To make 1, they could do 7 ÷ 7. To make 2 they could do (7 ÷ 7) + (7 ÷ 7) etc.
• This is a challenging game, but the winner is the player to achieve the most answers between 1 and 10.

Square root match

This activity can be done whole-class or in partners/small groups and allows students to practice finding square roots.

What you will need to play:

• Match cards (shown below)

How to play:

• Whole class
  • Shuffle match cards and distribute one to each student
  • Have students walk around the classroom and find their match (i.e., the student with “5” would partner up with the student whose card says “√25”
• Partners or small groups
  • Option 1: Students can work together to match up the cards 
  • Option 2: Students can flip all cards face down on a table and play “memory” – players take turns flipping over two cards. If they have a match, they keep the two cards. If they aren’t a match, they flip the cards back over and the next person goes. The winner is the player who ends up with the most matches at the end.

Example cards for printable resource:

\quad \sqrt{1} \quad	\quad 1 \quad	\quad \sqrt{4} \quad	\quad 2 \quad	\quad \sqrt{9} \quad	\quad 3 \quad
\quad \sqrt{16} \quad	\quad 4 \quad	\quad \sqrt{25} \quad	\quad 5 \quad	\quad \sqrt{36} \quad	\quad 6 \quad
\quad \sqrt{49} \quad	\quad 7 \quad	\quad \sqrt{64} \quad	\quad 8 \quad	\quad \sqrt{81} \quad	\quad 9 \quad
\quad \sqrt{100} \quad	\quad 10 \quad	\quad \sqrt{121} \quad	\quad 11 \quad	\quad \sqrt{144} \quad	\quad 12 \quad
\quad \sqrt{169} \quad	\quad 13 \quad	\quad \sqrt{196} \quad	\quad 14 \quad	\quad \sqrt{225} \quad	\quad 15 \quad

Exponent Game

This math game is similar to the card game “War,” but students use their cards to create and calculate exponents.

What you need to play:

• A partner (or a small group)
• A deck of playing cards (Number cards only; Ace can be used as 1)
  • Variation: Face cards can be used as an added challenge: A=1, J=11, Q=12, K=13

How to play:

• The cards should be shuffled and dealt evenly among the players
• Players should keep their stack of cards face down
• Each player flips two cards at the same time. The first card they flip is their base number and the second card flipped is the exponent. So, for example, if player 1 flips a 2 and then a 3, their number will be 2³ which equals 8. If their opponent flips a 4 and then a 2, their number will be 4² which equals 16. So player 2 wins that round.
• The player who wins each round collects all cards played during that round
• Whoever collects the most cards, wins!
• A challenging variation to this game would be to include four operation cards. These can be written on an index card or small piece of paper. As students create their two exponents, they can also draw an operation card. Then, students take turns adding, subtracting, multiplying, or dividing the two numbers.

Positive and negative cards game

This card game provides students with an opportunity to increase their understanding of positive and negative numbers during some friendly competition.

What you need to play:

• Deck of playing cards (number cards only)
  • Variation: add in face cards A=1, J=11, Q=12, K=13
• A partner or small group

How to play:

• In this game, the red cards represent negative numbers and the black cards are positive numbers
• Players shuffle the cards and deal them equally between themselves, keeping them face down
• All players place one card from their stack face-up at the same time
• Players can work together or take turns determining which card has the highest value. (Example: if there is a red 8 and a black 2, the black 2 has the highest value.)
• The player with the highest value card collects the four cards from that round
• When a player’s stack runs out, they should shuffle their collected cards and continue playing with those cards
• The first player to collect all the cards, wins!

Algebra Shop

During this activity, you will turn your classroom into a “market” and give students an opportunity to “buy” classroom items by writing algebraic expressions to represent their purchases.

What you need to play:

• Several classroom items labeled with a variable and a price on a sticky note.
  • Examples/ideas: 

• book, b, $4 
• pen, p, $0.25 
• desk, d, $8.25

• A piece of paper & pencil for each student
• One die for partners or small groups

How to play:

• Students will “shop” for the labeled items in the classroom market.
• Taking turns with their partner(s), each student will roll the dice. The dice will tell them how many of each item they will purchase. Then, students will write an algebraic equation representing each item. For example: if a student rolls a 5 for a book, they would write the expression 5b.
• Students should calculate their expressions: 5b = 5 ($4) = $20
• When they have purchased at least one of each item, they should write an expression representing their whole purchase. 5b + 4d, etc.
• Variations:
  • Students roll two dice to include higher quantities
  • Students go around the market twice (or more) and therefore, roll the dice more than one time per item. Therefore, if they rolled a 5 for the book on the first round, then a 3 on the second round, instead of 5b their expression would be 5b + 3b = 8b = 8($4) = $32

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by content team Vanessa Sipple-Asher and has since been revised and adapted for US schools by elementary math teacher Katie Keeton.