7 Questions You Should Ask When Reviewing Your Current Or Future Math Curriculum

Math leaders have many responsibilities. The foremost of these being student outcomes, staff development, assessment and reporting. Underpinning all of them is a robust math curriculum that serves as a comprehensive math solution.

Put plainly, if you don’t have good curriculum foundations it will be very hard to achieve successful outcomes. As mentioned in the article from Education Corner, you need to first look at your ‘intent’ in order to inform your ‘implementation’ and achieve high ‘impact’.

This guide offers actionable insights for leaders about what a good math curriculum looks like and how to choose the right math curriculum for your school or district.

The principles of a ‘good’ math curriculum

It’s actually pretty straightforward.

A good curriculum should have clear aims and objectives and should be communicated clearly and succinctly. Give careful thought to the scope and sequence of topics and the rationale for your curriculum model.

A weak curriculum is merely a list or timeline of units of work, independent from each other with limited interleaving.

A well-structured curriculum ensures that students develop conceptual understanding by building on their existing knowledge and experiences.

Here we take a look at a variety of curriculum models and the questions you should ask before choosing or delivering any effective math curriculum.

Top Tip: Look out for the checklist at the end.

Popular existing curriculum options

If you’re going to use a ready-made curriculum, there are a variety of existing options available. For example, math mastery, Illustrative Mathematics, Eureka Math, or Dreambox. These are presented as a full package of sequencing and curriculum maps, resources and assessments and professional development. The IM curriculum, for example, provides educators with the tools and professional learning necessary to implement effective instruction.

It’s also common for districts to author and implement their own curriculum to use across their area.

Where there is autonomy to decide on the curriculum, you might embrace a full package or cherry-pick from existing curricula to create a tailored offering.

Whether you opt for an off-the-shelf option or your own hybrid, you must have a clear rationale.

Questions to ask when reviewing your math curriculum 

1. How will you develop mastery and conceptual understanding within your math curriculum?

The basis of math mastery is teaching for conceptual understanding. This approach has become extremely popular in recent years.

Math Mastery is a teaching and student learning approach that focuses on the understanding of math concepts rather than rote memorization.

When a child can use their knowledge in problem solving and apply complex reasoning, this indicates they have mastered the concept. Influenced by East Asian approaches, a curriculum based on the principles of mastery have become extremely common, especially during the early stages in lower grades in elementary school.

These principles include:

• Representation and structure

• Mathematical thinking

• Fluency

• Variation theory

In math mastery instruction, concepts are ordered in a carefully structured sequence and students don’t progress to the next stage until they have mastered each one.

However, this approach can often conflict with grade structure, common core math and time pressures. It is crucial to consider how you can balance pace with mastery in your curriculum:

1. Map out a timeline to indicate how long to spend on a unit of work while considering the key concepts your students need to grasp.

2. Consider whether you require intervention or supplemental learning and how you can do this effectively. Intervention programs like Third Space Learning can help students gain significant growth, potentially achieving multiple years of progress in a single academic year.

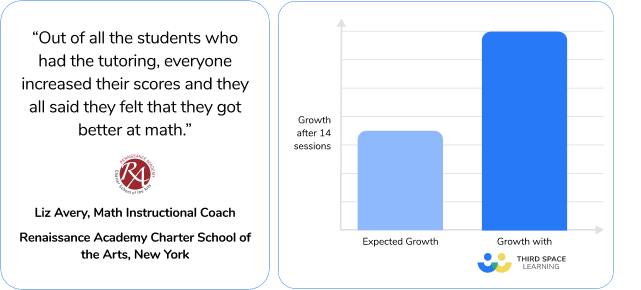
This will help balance pace and covering necessary content while ensuring that you explore mathematical concepts in sufficient depth for a seamless transition from, for example, Algebra 1 to Algebra 2 or middle school to high school mathematics programs.

2. Do you know the differences between curriculum models?

Think carefully about your curriculum model and why this is best for your students.

Model	Description	Advantages	Disadvantages
Mastery	Progression and sequence of curriculum builds on previous ideas. A topic is mastered before moving to the next stage.	Learners acquire depth of understanding and should move to the next stage with prerequisite skills.	Risk of not covering required curriculum.
Big ideas	Focusing on larger areas of the curriculum and drawing on related topics.E.g. Multiplicative reasoning (factors, multiplication facts and division facts, area), additive methods and place value (ordering two-digit numbers and three digit-numbers, standard form, decimal places and algebraic manipulation etc).	Supports students to make links with smaller topic areas. Supports interleaving of topics.	Math is a network of ideas rather than fitting on a linear scale of progression.Students may not develop prerequisite skills to enable them to interleave topics  early in the curriculum.
Spiral	Shorter units that alternate between topic areas (e.g. Algebra Unit 2: Inverse Operations, Place Value Unit 1: Whole Numbers, etc) and each time it is revisited, building on prior knowledge.You may teach the properties of shapes to draw 2-d shapes in the first unit and then move to 3-d shapes in the second, before revisiting both units in the third when teaching different orientations.	Frequent revisiting of skills.	Less likely to make links between topic areas. Can increase likelihood that math is viewed as a long list of topics and skills.
Topics	Focusing on embedding all of one branch of mathematics, e.g. number skills, before moving on to proportional reasoning, then algebra etc.Each branch is studied in its entirety, therefore potentially a whole year on just number skills for example, before studying any algebra.	Allows more space to ensure skills are mastered.	Limits scope to interleave topics early in the curriculum. Without extensive spaced retrieval practice, skills studied early in the curriculum can be forgotten.New students joining the school would miss entire branches of mathematics.

Whichever model you opt for, the sequencing and interleaving of topics needs careful consideration. Timing and scheduling units of work is a theme across any curriculum model. 

3. What is the context of your staff and student population?

Choosing a curriculum model depends on your context. For strong and stable teams of specialist math teachers with good subject knowledge, models such as mastery or big ideas provide an opportunity to teach mathematical concepts in depth. 

If your student population is transient, opt for a spiral curriculum rather than topics, as this provides an opportunity to frequently revisit topics with less reliance on prior knowledge.  

To deliver mastery and big ideas, ensure there is regular time for collaborative lesson planning to ensure teachers are confident with the required depth of conceptual understanding. 

Middle or high schools may want to liaise with feeder elementary schools to build on the foundations they have established, especially where schools have embedded a mastery curriculum.  

If you opt for a mastery curriculum you are likely going to require various manipulatives. This may provide an opportunity to utilize your existing resources to greater effect. Otherwise, you’ll need significant investment in apparatus.

4. How does the math curriculum build on previous grades and lay foundations for the future? 

As you would with a lesson, plan with the end in mind. Children’s math knowledge starts in elementary school and goes well beyond their high school diploma, so it is important to factor in progression from elementary to high school to real-world math!

Think of it as layers of planning, each stage zooming in with more detail.  Individual lessons should be thought as part of a bigger picture. This is the same when considering the sequencing of units of work and how it relates to the wider grade group.

When planning your high school math program, look back at the state standards for elementary school. This will give insight into which topics you can expect students to understand and which topics may need more attention.  

For example, geometry is not typically taught in high school until 10th grade. Students typically go through two years of pre-algebra and algebra, in 8th and 9th grade respectively, and may need a fresher when it comes to geometry in 10th grade.  

Reflecting on previous grade levels will help to inform your planning and scheduling as you think about what information might need consolidating and what may need more time to develop conceptual understanding. This will help to ensure that progress occurs at a suitable pace and that students remain engaged and challenged.

We also need to consider what we are preparing students for, aside from achieving great test results. You will need to consider the next pathways for students, be that employment, further or higher education.  

Not only may we need to prepare students to progress to higher study of math, but also subjects with significant statistical focus such as geography and psychology. 

When considering curriculum progression, think about your context.  Do you want to view the curriculum as separate entities for each grade level, or will you view it as a grade-level progression plan?

Whichever you decide, ensure you have a clear rationale for your choices and have accounted for enough development in earlier grade levels to equip students with skills for life rather than focusing on passing end of year tests.

5. How does your curriculum reflect pedagogy and cognitive science developments? 

There have been many recent developments in pedagogy and theory which are features and principles often incorporated into a curriculum and its resources.  

Third Space Learning’s series of blog posts around How I Wish I’d Taught Maths by Craig Barton covers many of these. Starting with this one on cognitive load theory.

Things to consider are:

• Variation theory: Variation theory covers a rigorous approach to question setting. Carefully selecting the progression of the questions asked, you encourage ‘intelligent practice’, reduce cognitive overload and, support reasoning and make connections. 

• Hinge questions: These are carefully considered questions which assist a teacher in diagnosing if a student or a class is ready to move on to the next stage. 

• Multiple choice questions: These should be diagnostic questions. The incorrect solutions need to be carefully considered to enable teachers to identify and address students’ common misconceptions. The correct answer should not be obvious from elimination.

• Spaced retrieval practice: Just because students grasped a concept at the time of teaching does not mean that this will remain the case.  Continually revisiting skills and concepts keeps them fresh in students’ minds so they can draw on them when required and reduce the need for intensive revision. 

• Interleaving: Students need to apply learning to unfamiliar contexts and by drawing on a range of skills to demonstrate mathematical ability.  Interleaving means that topics studied earlier in the curriculum are linked in to current learning to make links and revisit prior learning. Thinking about how topics can be revisited and interleaved. For example, when studying angle properties, forming and solving equations can be incorporated. As well as problems involving 2D and 3D shapes (knowing perpendicular lines bisect at right angles).

• Low stakes quizzing: Supporting the retrieval and providing effective formative assessment for learning, enabling teachers to be responsive. This can range from a short topic test completed in class to support feedback and future planning to multiple choice questions or starter questions.

• Metacognition: Metacognition is one of the most effective and least expensive interventions. Providing opportunities for students to reflect on their learning, their progress, and steps to improve can have dramatic results on their outcomes in math.

6. What are the support materials and resources for your math curriculum?

A curriculum needs to be clearly articulated to support teachers with their planning and implementation of the curriculum. And, it must ensure consistent, high-quality delivery.  

Therefore, information about a unit or series of lessons detailing the math skills and concepts, ideas for differentiation and misconceptions provides clarity and purpose to teachers’ planning rather than merely a series of presentation slides.

Think about incorporating the following materials:

• An overview of the year so that teachers understand the context, progression and timing of the concepts they are teaching.

• Unit overviews which contain information about the key objectives, representations, methods, misconceptions, suggestions for deep questions and resources.

• Assessments which range from low stakes quizzes in class to summative assessments which are likely to form the basis of reporting to parents.  You may opt for a topic diagnostic test and a topic test to assess the understanding to inform planning prior to the unit and assess the effectiveness of learning after it.

• Feedback and reflection are key parts of the assessment cycle. Following an assessment (high or low stakes), how do you support students to reflect on, improve and address misconceptions? In preparation for high stakes assessments, incorporate exam questions or a problem in context to solve questions later in a lesson.

• Starter activities, for example, interleaving review questions tailored to student needs. Use rich exploratory questions to set the scene for the lesson or exam questions.

• Lesson resources which include presentation slides, worksheets and activities, one-step and two-step questions, as well as multiple-choice questions. Think about what will ensure quality and support teachers with workload.  For example, providing quality deep questions, as these are resources that can be onerous to source or require more time, creativity and good subject knowledge to create.

• Knowledge organizers support students with self-study. Math requires practice rather than the recall of any given number fact but you may decide to incorporate knowledge organizers where it would support students with recall of facts where appropriate. 

Developing a robust curriculum is very complex. It requires a balance of providing depth, guidance and consistent high standards across a team of math teachers while embracing simplicity of structure and consistency so that the essence of the concepts are not lost.

7. How does the curriculum integrate technology to support teaching and learning?

In today’s digital age, integrating technology into the math curriculum is not just beneficial—it’s essential.

By leveraging technology, teachers can facilitate dynamic mathematical discussions, provide real-time feedback, and closely monitor student progress.

This integration empowers students to develop a deeper understanding of math concepts, build robust problem-solving skills, and achieve grade-level proficiency.

Whether through interactive simulations, online assessments, or digital manipulatives, technology is pivotal in making math learning more accessible and effective.

Communicating and sharing your curriculum

A good curriculum will only be effective if the team implements it well. Therefore, communication is key. Communicate the following:

• Key objectives students need to understand.

• Time scales as a guideline to achieve mastery while maintaining pace to ensure delivery ofthe curriculum.

• Common teaching approaches. Specific approaches should be common across the school, such as bar modeling when teaching addition, subtraction, multiplication and division problems.

• Representation and methods: which topics require mental methods and which formal written methods? Are statistics lessons going to include bar charts, pictograms, etc?

• Outline of the resources available.

• Differentiation ideas.

• Summary of potential misconceptions.

• Prior learning and next steps.

• Homework links – either suggested resources or clip numbers and links if you use an online homework platform such as Zearn.

Teachers are busy so this information must be concise, accessible and an integral part of daily planning practice. I have found that a unit overview, a one-page document per unit summarizing the key information is valuable.

Bring these to planning meetings, encourage staff to annotate and reflect on them, promote engagement with time to discuss and amend for future use.

Although strong resources and presentation slides ensure consistent delivery of a curriculum, supporting documents to ensure clarity are essential too. 

Checklist for any new curriculum to ensure grade level proficiency

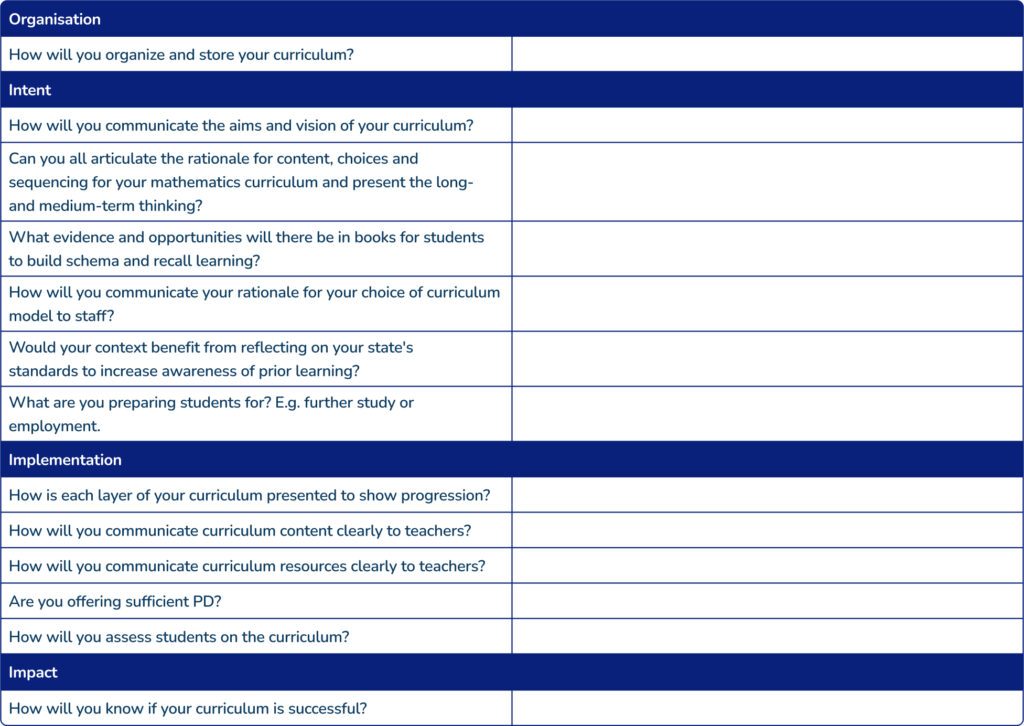
Here is a checklist of things you may want to consider and discuss with your colleagues regarding any curriculum change. Documenting agreed responses is always a good idea.

• Storage and presentation of your curriculum: in an increasingly digital world, this is likely to be stored online. But, how can you efficiently organize this?

• Statement of intent: How will you communicate the aims and vision of your curriculum?

• Can you articulate the rationale for content choices and sequencing for your mathematics curriculum? Can you present the long- and medium-term thinking? Concise unit overviews and road maps for the year can be very useful. 

• What evidence and opportunities will there be in books for students to build schema and recall learning?

• Buy-in from staff: How will you communicate your rationale for your choice of curriculum model?

• Would your context benefit from reflecting on your state’s standards to increase awareness of prior learning?

• What are you preparing students for? E.g. further study or employment.

• Implementation: How do you present and show progression in each layer of your curriculum? E.g. using a curriculum map or flight path? This is where you think about the sequencing and timing of topics to prepare students to achieve top grades and equip them with the necessary skills for their next stages.

• Communication and sharing of content: How will you communicate clearly to teachers?

• Math resources to support your curriculum: How will you communicate clearly to teachers? 

• Professional learning program to support effective delivery.

• Assessment: how will you assess students on the curriculum? This could include high order thinking questions, low-stakes quizzing and summative assessments.

• Impact: How will you know if your curriculum is successful? Look beyond student assessment data. Consider how you can capture staff and student voice and review effectiveness from learning walks.

Final thoughts on your math curriculum

Life is always full of new challenges in education. Priorities shift, the state standards are audited and modified, and pandemics occur… 

It is impossible to account for every eventuality but as recent events have shown, whether delivered online, at home, or at school, a strong and effective curriculum which is understood by everyone from leaders to staff, students and parents, can prove to be an essential uniting focus when everything else seems so uncertain! 

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by secondary math teacher Lindsey Ford and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.