High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Factors and multiples Multiplying multi digit numbers Place valueDistributive property
Here you will learn about the distributive property, including what it is, and how to use it to solve problems.
Students will first learn about the distributive property as part of operations and algebraic thinking in 3rd grade.
What is the distributive property?
The distributive property states that multiplying the sum of two or more numbers is the same as multiplying the addends separately.
For example,
When multiplying 2 \times 8, you can break 8 up into 2 + 6.
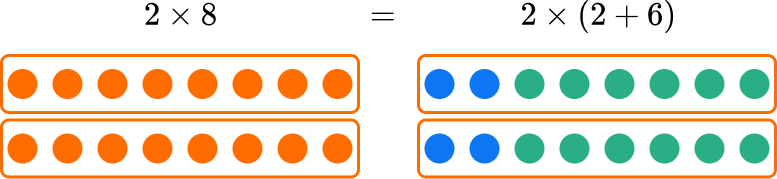
The distributive property says that you can multiply the parts separately and then add the products together.
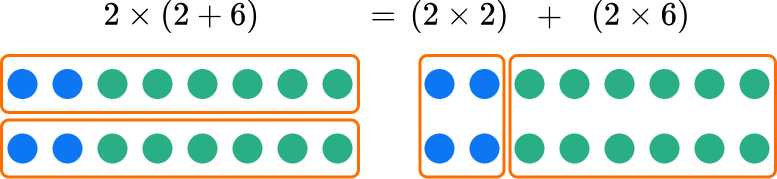
Any way you solve the equivalent expressions, the product is the same.
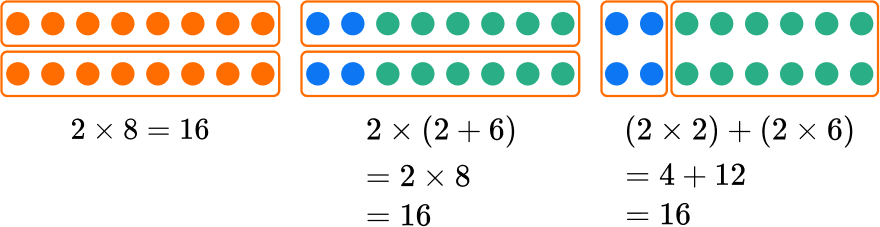
For most expressions, there is more than one way to use the distributive property.
For example,
When multiplying 2 \times 8, you can break 8 up into 5 + 3.
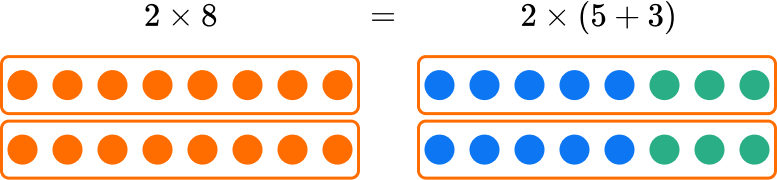
The distributive property says that you can multiply the parts separately and then add the products together.
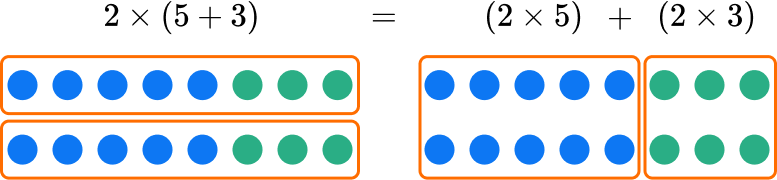
Any way you solve the equivalent expressions, the product is the same.
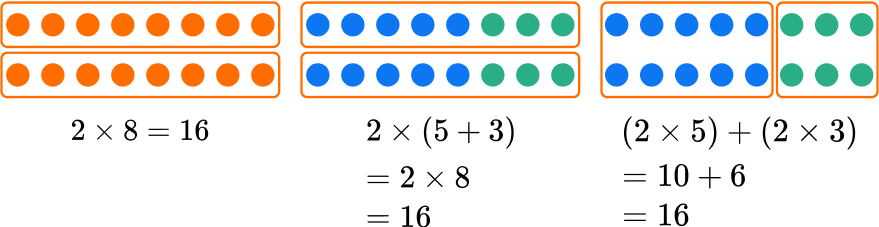
What is the distributive property?

![[FREE] Distributive Property Worksheet (Grade 3)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Distributive-Property-Worksheet-listing-image.png)
[FREE] Distributive Property Worksheet (Grade 3)
![[FREE] Distributive Property Worksheet (Grade 3)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Distributive-Property-Worksheet-listing-image.png)
Check your 3rd grade students’ understanding of distributive property and how to use it to solve problems. Includes 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Distributive Property Worksheet (Grade 3)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Distributive-Property-Worksheet-listing-image.png)
[FREE] Distributive Property Worksheet (Grade 3)
![[FREE] Distributive Property Worksheet (Grade 3)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Distributive-Property-Worksheet-listing-image.png)
Check your 3rd grade students’ understanding of distributive property and how to use it to solve problems. Includes 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this property relate to 3rd grade math?
- Grade 3 – Operations and Algebraic Thinking (3.OA.B.5)
Apply properties of operations as strategies to multiply and divide.
Examples: If 6 \times 4 = 24 is known, then 4 \times 6 = 24 is also known. (Commutative property of multiplication.)
3 \times 5 \times 2 can be found by 3 \times 5 = 15, then 15 \times 2 = 30, or by 5 \times 2 = 10, then 3 \times 10 = 30. (Associative property of multiplication.)
Knowing that 8 \times 5 = 40 and 8 \times 2 = 16, one can find 8 \times 7 as 8 \times (5 + 2) = (8 \times 5) + (8 \times 2) = 40 + 16 = 56. (Distributive property.)
How to use the distributive property
- Identify an equation multiplying two numbers.
- Show one of the numbers being multiplied as a sum of numbers.
- Multiply each number in the sum.
- Add the partial products together to find the final product.
Distributive property examples
Example 1: distributive property with basic facts
Show how to solve 3 \times 5 using the distributive property.
- Identify an equation multiplying two numbers.
You can use the distributive property with 3 \times 5, since it is multiplication.
2Show one of the numbers being multiplied as a sum of numbers.
Either number can be used, but for this example let’s break up 5 into 4 + 1.
3 \times 5=3 \times(4+1)
3Multiply each number in the sum.
\begin{aligned} & 3 \times(4+1) \\\\ & =(3 \times 4)+(3 \times 1) \\\\ & =12+3 \end{aligned}
4Add the partial products together to find the final product.
12 + 3 = 15
3 \times 5=15 can be solved using the distributive property.
Example 2: distributive property with basic facts
Show how to solve 12 \times 9 using the distributive property.
Identify an equation multiplying two numbers.
You can use the distributive property with 12 \times 9, since it is multiplication.
Show one of the numbers being multiplied as a sum of numbers.
Either number can be used, but for this example let’s break up 9 into 3 + 3 + 3.
12 \times 9=12 \times(3+3+3)
Multiply each number in the sum.
\begin{aligned} & 12 \times(3+3+3) \\\\ & =(12 \times 3)+(12 \times 3)+(12 \times 3) \\\\ & =36+36+36 \end{aligned}
Add the partial products together to find the final product.
36 + 36 + 36 = 108
12 \times 9=108 can be solved using the distributive property.
Example 3: distributive property with basic facts
Show how to solve 7 \times 6 using the distributive property.
Identify an equation multiplying two numbers.
You can use the distributive property with 7 \times 6, since it is multiplication.
Show one of the numbers being multiplied as a sum of numbers.
Either number can be used, but for this example let’s break up 7 into 4 + 3.
7 \times 6=(4+3) \times 6
Multiply each number in the sum.
\begin{aligned} & (4+3) \times 6 \\\\ & =(4 \times 6)+(3 \times 6) \\\\ & =24+18 \end{aligned}
Add the partial products together to find the final product.
24 + 18 = 42
7 \times 6=42 can be solved using the distributive property.
Example 4: distributive property with basic facts
Show how to solve 4 \times 11 using the distributive property.
Identify an equation multiplying two numbers.
You can use the distributive property with 4 \times 11, since it is multiplication.
Show one of the numbers being multiplied as a sum of numbers.
Either number can be used, but for this example let’s break up 11 into 10 + 1.
4 \times 11=4 \times(10+1)
Multiply each number in the sum.
\begin{aligned} & 4 \times(10+1) \\\\ & =(4 \times 10)+(4 \times 1) \\\\ & =40+4 \end{aligned}
Add the partial products together to find the final product.
40 + 4 = 44
4 \times 11=44 can be solved using the distributive property.
Example 5: distributive property with basic facts
Show how to solve 8 \times 5 using the distributive property.
Identify an equation multiplying two numbers.
You can use the distributive property with 8 \times 5, since it is multiplication.
Show one of the numbers being multiplied as a sum of numbers.
Either number can be used, but for this example let’s break up 8 into 2 + 6.
8 \times 5=(2+6) \times 5
Multiply each number in the sum.
\begin{aligned} & (2+6) \times 5 \\\\ & =(2 \times 5)+(6 \times 5) \\\\ & =10+30 \end{aligned}
Add the partial products together to find the final product.
10 + 30 = 40
8 \times 5=40 can be solved using the distributive property.
Example 6: distributive property with basic facts
Show how to solve 3 \times 12 using the distributive property.
Identify an equation multiplying two numbers.
You can use the distributive property with 3 \times 12, since it is multiplication.
Show one of the numbers being multiplied as a sum of numbers.
Either number can be used, but for this example let’s break up 12 into 1 + 1 + 10.
3 \times 12=3 \times(1+1+10)
Multiply each number in the sum.
\begin{aligned} & 3 \times(1+1+10) \\\\ & =(3 \times 1)+(3 \times 1)+(3 \times 10) \\\\ & =3+3+30 \end{aligned}
Add the partial products together to find the final product.
3 + 3 + 30 = 36
3 \times 12=36 can be solved using the distributive property.
![[FREE] Distributive Property Worksheet (Grade 3)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Distributive-Property-Worksheet-listing-image.png)
[FREE] Distributive Property Worksheet (Grade 3)
![[FREE] Distributive Property Worksheet (Grade 3)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Distributive-Property-Worksheet-listing-image.png)
Check your 3rd grade students’ understanding of distributive property and how to use it to solve problems. Includes 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Distributive Property Worksheet (Grade 3)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Distributive-Property-Worksheet-listing-image.png)
[FREE] Distributive Property Worksheet (Grade 3)
![[FREE] Distributive Property Worksheet (Grade 3)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Distributive-Property-Worksheet-listing-image.png)
Check your 3rd grade students’ understanding of distributive property and how to use it to solve problems. Includes 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREETeaching tips for the distributive property
- Intentionally choose practice problems that lend themselves to being solved with the distributive property, as it is not always necessary or useful in all solving situations. As students becoming more comfortable with the topic, show an example of the distributive property with more complex numbers (ex. with decimals) and solve together.
- Instead of just giving students the distributive property definition, draw attention to examples of the property as they come up in daily math activities. You may even keep an anchor chart of different examples. Over time, students will start using it and recognizing it on their own and then you can introduce them to the distributive property and its official definition through their own examples.
- Include plenty of student discourse around this topic to ensure that students understand that breaking apart a number and then multiplying it in parts does not change the total product. This could include students sharing their thinking or critiquing the thinking of others.
Easy mistakes to make
- Thinking there is only one way to use the distributive property to solve
Often, there is more than one way to solve using the distributive property to obtain the correct answer.
For example,
\begin{aligned} & 4 \times 5 \hspace{4.65cm} 4 \times 5 \\ & =(2+2) \times 5 \hspace{3.5cm} =(1+3) \times 5 \\ & =(2 \times 5)+(2 \times 5) \hspace{1cm} \text{ OR } \hspace{1cm} =(1 \times 5)+(3 \times 5) \\ & =10+10 \hspace{3.9cm} =5+15 \\ & =20 \hspace{4.63cm} =20 \end{aligned}
- Decomposing with multiplication instead of addition
To use the distributive property, break apart a number being multiplied with addition. Using multiplication can lead to the incorrect answer.
For example,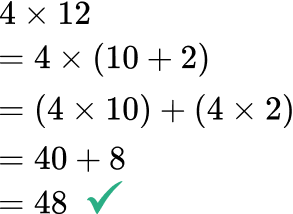 \hspace{1cm} \text{ OR } \hspace{1.1cm}
\hspace{1cm} \text{ OR } \hspace{1.1cm} 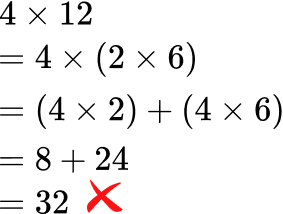
- Not decomposing by place value
To use the distributive property, break apart a number being multiplied in a way that keeps the overall value the same. This includes preserving place value. Otherwise the products will not be equivalent.
For example,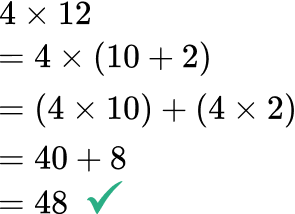 \hspace{1cm} \text{ OR } \hspace{1.1cm}
\hspace{1cm} \text{ OR } \hspace{1.1cm} 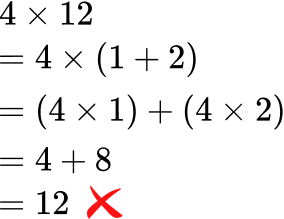
Related properties of equality lessons
Practice questions
1. Which of the following equations shows 12 \times 6 using the distributive property?




The numbers are being multiplied, so the distributive property can be used.
\begin{aligned} & 12 \times 6 \\\\ & =12 \times(3+3) \hspace{1.2cm} \text{ *Break 6 up into 3 + 3}\\\\ & =(12 \times 3)+(12 \times 3) \hspace{0.3cm} \text{ *Multiply each 3 by 12} \\\\ & =36+36 \hspace{1.8cm} \text{ *Add the partial products back together} \\\\ & =72 \end{aligned}
2. Which of the following equations shows 7 \times 9 using the distributive property?




The numbers are being multiplied, so the distributive property can be used.
\begin{aligned} & 7 \times 9 \\\\ & =(4+3) \times 9 \hspace{1.2cm} \text{ *Break 7 up into 4 + 3}\\\\ & =(4 \times 9)+(3 \times 9) \hspace{0.4cm} \text{ *Multiply both 4 and 3 by 9} \\\\ & =36+27 \hspace{1.6cm} \text{ *Add the partial products back together} \\\\ & =63 \end{aligned}
3. Which of the following equations shows 11 \times 8 using the distributive property?




The numbers are being multiplied, so the distributive property can be used.
\begin{aligned} & 11 \times 8 \\\\ & =(1+10) \times 8 \hspace{1.1cm} \text{ *Break 11 up into 1 + 10}\\\\ & =(1 \times 8)+(10 \times 8) \hspace{0.3cm} \text{ *Multiply both 1 and 10 by 8} \\\\ & =8+80 \hspace{1.8cm} \text{ *Add the partial products back together} \\\\ & =88 \end{aligned}
4. Which of the following equations shows 3 \times 7 using the distributive property?




The numbers are being multiplied, so the distributive property can be used.
\begin{aligned} & 3 \times 7 \\\\ & =3 \times(1+3+3) \hspace{1.8cm} \text{ *Break 7 up into 1 + 3 + 3}\\\\ & =(3 \times 1)+(3 \times 3)+(3 \times 3) \hspace{0.3cm} \text{ *Multiply 1, 3 and 3 by 3} \\\\ & =3+9+9 \hspace{2.6cm} \text{ *Add the partial products back together} \\\\ & =21 \end{aligned}
5. Which of the following equations is NOT a way to solve 10 \times 5 using the distributive property?




This strategy is NOT a way to solve with the distributive property.
All the other equations break 10 or 5 up into a sum and add the products of the parts, using the distributive property correctly:
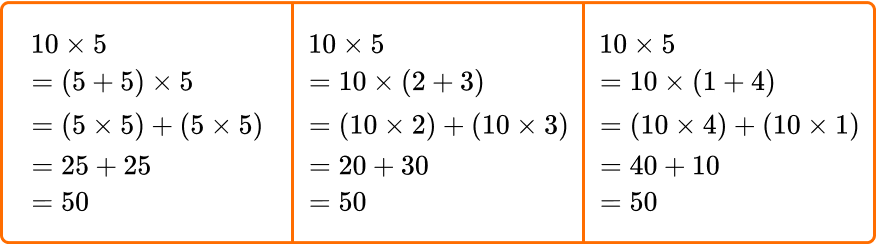
6. Which of the following equations is NOT a way to solve 9 \times 8 using the distributive property?




This strategy is NOT a way to solve 9 \times 8 with the distributive property.
All the other equations break 9 or 8 up into a sum and add the products of the parts, using the distributive property correctly:
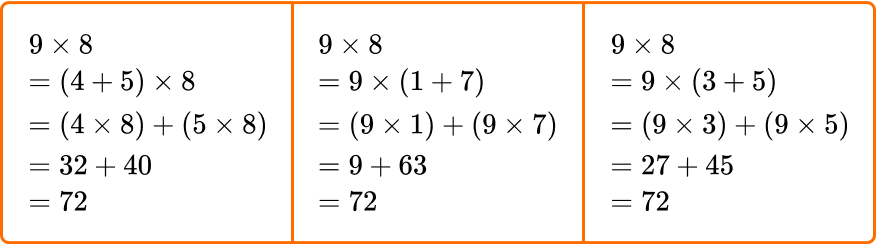
FAQs
Yes, the distributive property can be used with integers (including negative numbers) and rational numbers (including fractions and decimals), as long as the numbers are all being multiplied. In middle and high school, students will learn how to use the distributive property with any real number and/or algebraic expression.
No, even though the associative property also uses parentheses, they are different properties. The associative property says you can change the grouping of numbers when adding or multiplying and the sum or product will be the same.
Yes, this is called the distributive property of multiplication over subtraction. The examples shown in this topic guide use the distributive property of multiplication over addition.
This is a general term and means the same as the distributive property.
No, because of the order of operations (or PEMDAS), the products will be found first and then added together. However, it is good practice to group each partial product with parentheses.
Students will use the distributive property in solving more complex problems, such as multiplying two binomials together.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!