High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Pythagorean Theorem Literal equations Right trianglesTrigonometry
Here you will learn about Trigonometry including how to use right triangle trigonometry(SOHCAHTOA), inverse trigonometric functions, and exact trigonometric values. You will also learn about the sine rule, the cosine rule, how to find the area of a triangle using \cfrac{1}{2} \, ab \sin(C) and lastly, verify trigonometric identities.
Students first learn about trigonometry in algebra II and expand their knowledge as they progress through precalculus and calculus.
What is trigonometry?
Trigonometry is a branch of mathematics that focuses on triangles. Specifically, the relationship between the angles and sides of triangles. Trigonometry is derived from the Greek word “trigonon” meaning triangle and “metron” meaning to measure.
There are three main functions of trigonometry.
- Sine function \rightarrow \sin
- Cosine function \rightarrow \cos
- Tangent function \rightarrow \tan
However, in higher levels of mathematics, the use of trigonometry extends beyond triangles, in particular, when verifying trigonometric identities, the unit circle and the graphs of trigonometric functions.
Trigonometric relationships are crucial for higher levels of mathematics as well as physics, engineering, astronomy, and even in art fields such as music.
![[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)
![[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 9 to 12 students’ understanding of Trigonometry. 15+ questions with answers covering a range of 9th to 12th grade trigonometry topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)
![[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 9 to 12 students’ understanding of Trigonometry. 15+ questions with answers covering a range of 9th to 12th grade trigonometry topics to identify areas of strength and support!
DOWNLOAD FREESOHCAHTOA
SOHCAHTOA is a mnemonic device that gives you an easy way to remember the three main trigonometric ratios of the sides of a right triangle.
The trig ratios are used to find the missing sides of the triangle (right triangle) and the missing acute angles.
The names of the three ratios are:
- Sine (Sin)
- Cosine (Cos)
- Tangent (Tan)

When writing the trigonometric ratios, you must write them with respect to one of the acute angles of the right triangle. Let’s use Angle A to write the ratios.
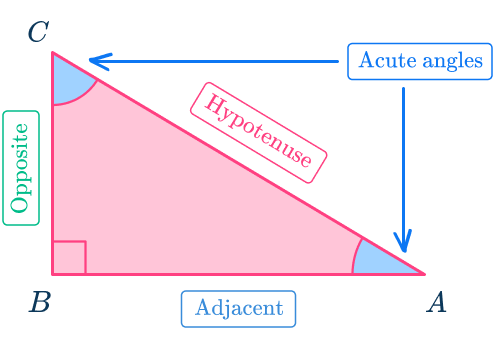
The Sine ratio with respect to acute angle A=\sin A=\frac{ \text{opposite side length}} {\text{hypotenuse length}}
The Cosine ratio with respect to acute angle A=\cos A=\frac{\text{adjacent side length}}{\text{hypotenuse length}}
The Tangent ratio with respect to acute angle A=\tan A=\frac{\text{opposite side length}}{\text{adjacent side length}}
For example, let’s use SOHCAHTOA to find the missing side length of the triangle below.
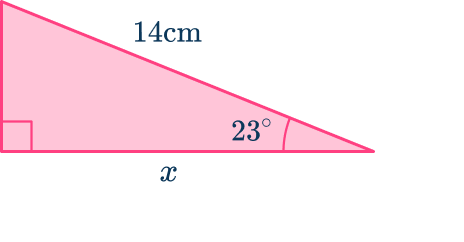
Using the angle marked as 23^{\circ} and the hypotenuse, to find x, use the cosine function because cosine is \frac{\text{adjacent side length}}{\text{hypotenuse length}}.
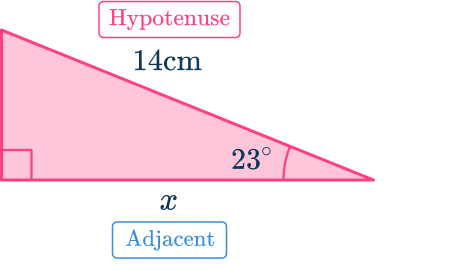
The equation to solve for x is:
\cos 23=\cfrac{x}{14}Solve for x by multiplying both sides of the equation by 14.
14 \times \cos 23=xThen, use a calculator to find the value of x (round the answer to the nearest tenth).
x=12.9You can use SOHCAHTOA to calculate lengths and angles in 2D figures (like the example above) and 3D shapes by recognizing right-angle triangles.
For example, we can find the length AC of a parallelogram or the length AH in the cuboid below.
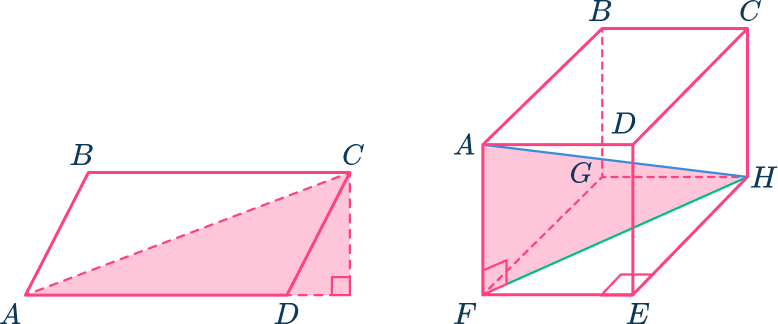
Step-by-step guide: SOHCAHTOA
Trig functions
The sine, cosine, and tangent are the main trigonometric functions. However, there are three other trigonometric functions that are used to find missing values.
- Cosecant function \rightarrow \text {abbreviated csc}
- Secant function \rightarrow \text {abbreviated sec}
- Cotangent function \rightarrow \text {abbreviated cot}
These functions are directly related to the sine, cosine and tangent functions.
Let’s look at the triangle below to write the trigonometric ratios with respect to the angle marked as \theta.
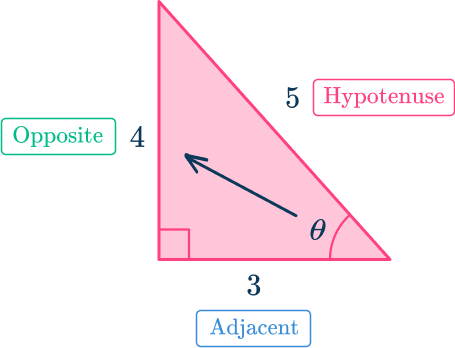
Using SOHCAHTOA:
\sin \theta=\cfrac{4}{5} \cos \theta=\cfrac{3}{5} \tan \theta=\cfrac{4}{3}The cosecant, secant, and cotangent are reciprocals of the sine, cosine, and tangent, respectively.
\begin{aligned}& \sin \theta=\cfrac{4}{5} \rightarrow \csc \theta=\cfrac{5}{4} \\\\ & \cos \theta=\cfrac{3}{5} \rightarrow \sec \theta=\cfrac{5}{3} \\\\ & \tan \theta=\cfrac{4}{5} \rightarrow \cot \theta=\cfrac{5}{4} \end{aligned}Step-by-step guide: Trig functions
Inverse trig functions
Inverse trigonometric functions allow us to calculate the size of an angle in a right-angle triangle. The inverse trig functions are expressed as this:

For example, let’s look at the triangle below.
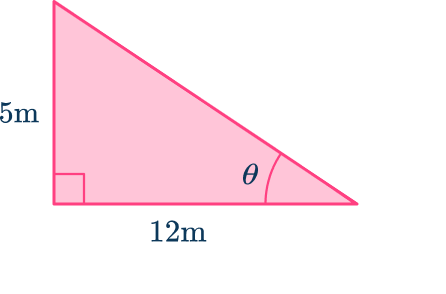
Instead of solving for a side measurement, you need to solve for the angle, \theta. In order to do this, you need to use the inverse trig function. The given side values represent the opposite side and the adjacent side (with respect to \theta ).
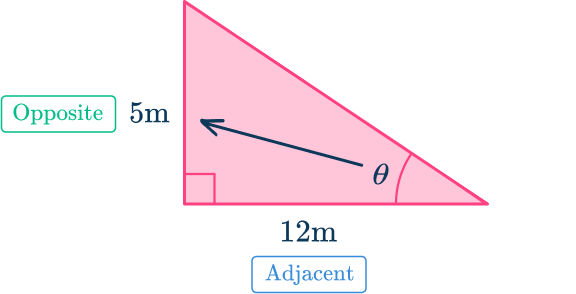
The equation to find \theta is:
\tan \, \theta=\cfrac{5}{12}In order to solve for \theta, you must use the inverse tan function (\tan ^{-1})
\theta=\tan ^{-1}\left(\cfrac{5}{12}\right)Type this into a calculator to find the value of \theta.
\theta=\tan ^{-1}\left(\cfrac{5}{12}\right) \approx 22.6199Rounding the answer to the nearest tenth, \theta=22.6^{\circ}.
Step-by-step guide: Sin cos tan
Exact values of trig functions
Exact trigonometric values are found when the relationships between the sides and the angles in a triangle have exact values.
Here are the exact trigonometric values for sine, cosine and tangent for angles in the first quadrant, 0^{\circ} \leqslant \theta \leqslant 90^{\circ}.
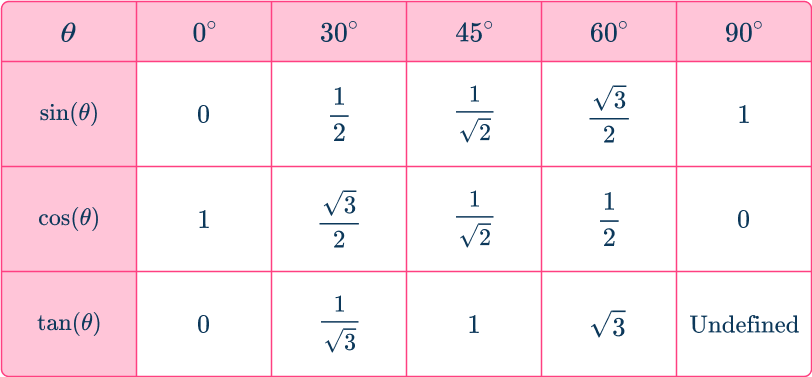
However, you can use those values to find the exact values of trig functions where the angles are not in the first quadrant by using the reference angle.

Also, the sign value of the angles can be found by the following:

Using the information above, let’s find the exact value of \cos 150^{\circ}
150^{\circ} is a second quadrant angle. So, to find the reference angle subtract 150 from 180.
180-150=30The reference angle to 150^{\circ} is 30^{\circ} , which means the \cos 150^{\circ} behaves similarly to \cos 30^{\circ}.
You know that the exact value of \cos 30^{\circ}=\cfrac{\sqrt{3}}{2}, you also know that the cosine is not positive in Quadrant II. So, the exact value of \cos 150^{\circ}=\cfrac{\sqrt{3}}{2}.
Step-by-step guide: How to find the exact value of a trig function
Step-by-step guide: Trig table
Solving non-right triangles
The ratios of the sides of a right triangle, SOHCAHTOA, are used to find missing angles and sides of only right triangles. So when the triangle is not a right triangle, you have to rely on other strategies to find missing sides and angles.
- Law of Sines (Sine rule): The sine rule (or the law of sines) is a relationship between the size of an angle in a triangle and the opposite side. The Law of Sines is typically used when you are given values of a triangle that are in the form of angle-side-angle or angle-angle-side.
The law of sines is given to be:
\cfrac{\sin A}{a}=\cfrac{\sin B}{b}=\cfrac{\sin C}{c}
Let’s use the Law of Sines to find side a in triangle ABC.
Note: Side a is across from angle A.
Notice how the triangle has an angle-angle-side set up, meaning that you are given angle-angle-side values.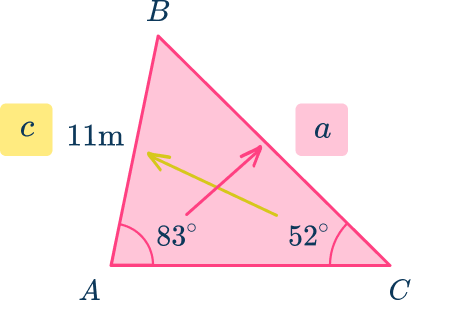
The equation to use to find side a is:
\begin{aligned}& \cfrac{\sin A}{a}=\cfrac{\sin C}{c} \\\\ & \cfrac{\sin 83}{a}=\cfrac{\sin 52}{11} \end{aligned}
Solve the proportional relationship by cross multiplying.
\begin{aligned}& 11 \times \sin 83=a \times \sin 52 \\\\ & \cfrac{11 \times \sin 83}{\sin 52}=a \end{aligned}
Use a calculator to find the value of a.
13.8552 \approx a
Round the answer to the nearest tenth, a=13.9 m
- Law of Cosines (Cosine rule): The cosine rule (or the law of cosines) is another formula which can be used to calculate a missing side or angle of a non-right angle triangle. The Law of Cosines is typically used when you are given values of a triangle that are in the form of side-side-side or side-angle-side.
The Law of Cosines is given to be:
\begin{aligned}& a^2=b^2+c^2-2 b c \cos (A) \\\\ & b^2=a^2+c^2-2 a c \cos (B) \\\\ & c^2=a^2+b^2-2 a b \cos (C) \end{aligned}
Let’s find the value of side a using the law of cosines.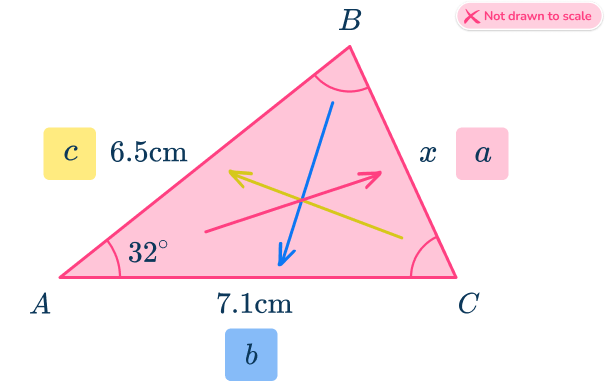
Since you need to solve for side x which is side a, use:
a^2=b^2+c^2-2 b c \cos (A) (round the answer to the nearest hundredth)
\begin{aligned}x^{2}&=7.1^{2}+6.5^{2}-2\times7.1\times6.5\times\cos(32) \\\\ x^{2}&=50.41+42.25-92.3\times\cos(32) \\\\ x^{2}&=14.38516072… \\\\ x&=\sqrt{14.38516072…} \\\\ x&=3.79 \, cm\quad(2dp) \end{aligned}
Step-by-step guide: Law of Sines
Step-by-step guide: Law of Cosines
Area of a triangle
Through elementary school and middle school you learn how to find the area of a triangle using the formula, A=\cfrac{1}{2} \, b h.
Now that you know how to use trigonometric functions, there is another way to find the area of a triangle.
\begin{aligned}& A=\cfrac{1}{2} \, a b \sin (C) \\\\ & A=\cfrac{1}{2} \, a c \sin (B) \\\\ & A=\cfrac{1}{2} \, b c \sin (A) \end{aligned}Let’s use the new formula to calculate the area of triangle ABC.
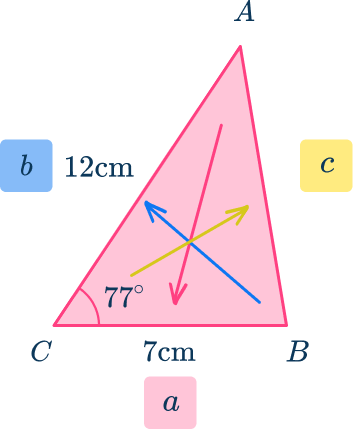
Since Angle C is given, use this formula:
A=\cfrac{1}{2} \, ab \sin(C)Substitute in the given values.
\begin{aligned}A&=\cfrac{1}{2} \, ab\sin(C) \\\\ A&=\cfrac{1}{2} \, (12\times7\times\sin(77)) \\\\ A&=\cfrac{81.84708544}{2} \\\\ A&=40.92 \, cm^{2}\quad(2dp) \end{aligned}The area of triangle ABC rounded to the nearest hundredth is 40.92 \mathrm{~cm}^2.
Step-by-step guide: Trig formula for area of a triangle
Trig identities
Trigonometric identities are mathematical equations that involve trigonometric functions, like sine, cosine, and tangent and they are true for all values of the variables involved.
An identity is an equation that is always true.
Let’s verify that the following identity is true:
\cfrac{\sin (\theta)}{\cos (\theta)} \equiv \tan (\theta)When verifying an identity choose one of the equations to work with and leave the other side alone. There are multiple ways to verify a trig identity. In this case, let’s use the SOHCAHTOA relationships.
\begin{aligned}& \sin \theta=\cfrac{o}{h} \\\\ & \cos \theta=\cfrac{a}{h}\end{aligned}Rewriting the left hand side of the identity to be,
\begin{aligned}& \cfrac{\sin (\theta)}{\cos (\theta)} \equiv \tan (\theta) \\\\ & \cfrac{\cfrac{o}{h}}{\cfrac{a}{h}}=\tan \theta \\\\ & \cfrac{o}{h} \times \cfrac{h}{a}=\tan \theta \end{aligned}\cfrac{o}{a}=\tan \theta (This is true, the tangent ratio is equal to the opposite side divided by the adjacent side)

Step-by-step guide: Trig identities
Step-by-step guide: Trig formulas
What is trigonometry?
Common Core State Standards
How does this apply to high school math?
- High School Functions – Trigonometric Functions (HSF-TF.C.8)
Prove the Pythagorean identity \sin^{2}(\theta)+\cos^{2}(\theta)=1 and use it to find \sin(\theta), \cos(\theta), or \tan(\theta) given \sin(\theta), \cos(\theta), or \tan(\theta) and the quadrant of the angle.
- High School Geometry – Similarity, Right Triangles, and Trigonometry HSG-SRT.C.6
Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.
- High School Geometry – Similarity, Right Triangles, and Trigonometry HSG-SRT.C.8
Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
- High School Geometry – Similarity, Right Triangles, and Trigonometry – HSG-SRT.D.10 (+)
Prove the Laws of Sines and Cosines and use them to solve problems.
- High School Geometry – Similarity, Right Triangles, and Trigonometry – HSG-SRT.D.11 (+)
Understand and apply the Law of Sines and the Law of Cosines to find unknown measurements in right and non-right triangles (e.g., surveying problems, resultant forces).
How to solve trigonometry problems
If you want more detailed steps and practice for solving for the sides and angles of right triangles and non-right triangles, finding the exact value of trig functions, and working with trig identities and formulas, check out the links highlighted above or take a look at the examples below.
Trigonometry examples
Example 1: SOHCAHTOA
Find the measure of side a.
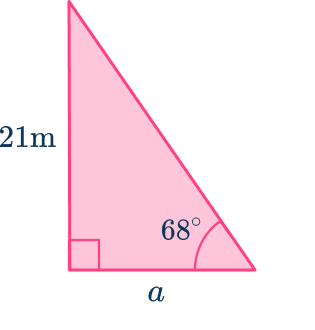
- Identify the trig ratio to use.
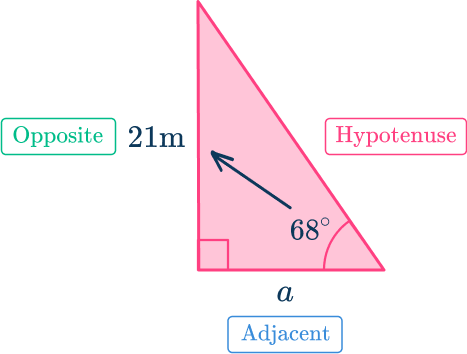
Since you need to solve for the adjacent side and you are given the opposite side, use the tangent ratio.
\text { tangent ratio }=\cfrac{\text { opposite side }}{\text { adjacent side }}2Write an equation to find the missing part.
\tan 68=\cfrac{21}{a}3Solve for the missing part.
In this case, multiply both sides by a.
a \times \tan 68=21Then divide by \tan 68.
a=\cfrac{21}{\tan 68}Calculate the value of a with a calculator.
a=8.484551Round the answer to the nearest hundredth, 8.48 \, m.
Example 2: inverse function
Find the measure of angle \theta.
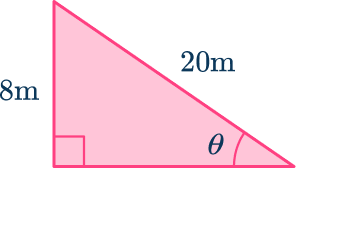
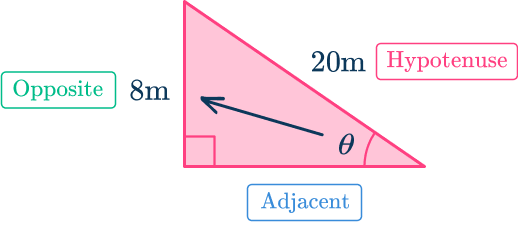
You are given the opposite side and the hypotenuse, so use the sine ratio.
\text { sine ratio }=\cfrac{\text { opposite side }}{\text { hypotenuse }}
Use the inverse sine function to find the value of \theta.
\begin{aligned}& \sin \theta=\cfrac{8}{20} \\\\
& \theta=\sin ^{-1}\left(\cfrac{8}{20}\right) \end{aligned}
Type into a calculator to get the value of \theta.
\theta=23.5782 (round the answer to the nearest hundredth)
\theta=23.58^{\circ}
Example 3: Law of Sines
Find the value of angle A.
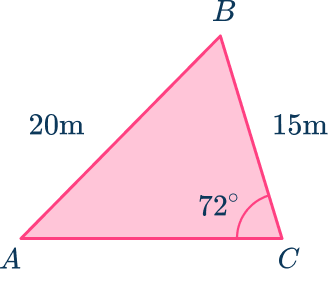
In this case, you are given angle C , side c, and side a. Since you need to solve for angle A, use the sine rule (Law of Sines).
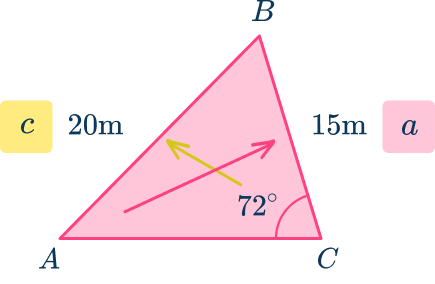
It’s also a SSA set up which lends itself to the law of sines.
\cfrac{\sin A}{15}=\cfrac{\sin 72}{20} \quad (cross multiply)
\begin{aligned}& 20 \times \sin A=15 \times \sin 72 \\\\
& \sin A=\cfrac{15 \times \sin 72}{20} \\\\
& \sin A=0.713292 \end{aligned}
Use the inverse sine function to find angle A.
\text { Angle } A=45.50^{\circ}
Example 4: exact value
Find the exact value of \sin 330^{\circ} .
330^{\circ} is a 4 th quadrant angle and the sine has a negative value in the 4 th quadrant.
To find the reference angle when the original angle is in the 4 th quadrant, subtract the angle from 360.
360-330=30
The reference angle is 30^{\circ}.
Since the sine is negative in the 4 th quadrant and the \sin 30=\cfrac{1}{2}, then \sin 330=- \, \cfrac{1}{2}.
Example 5: area of triangle
Find the area of the triangle below.
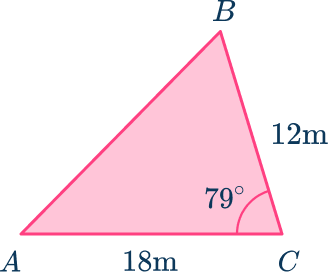
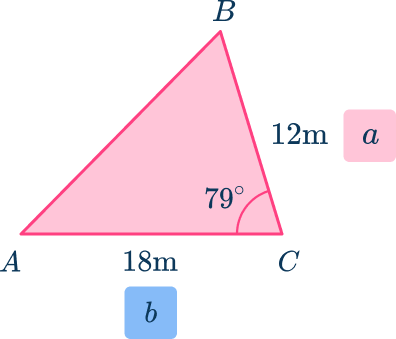
Since you are given the values of side a, b, and angle C, use A=\cfrac{1}{2} \, b c \sin C
A=\cfrac{1}{2}(18)(12) \sin 79
Example 6: verify the identity
Verify the identity.
\sin \theta \cot \theta \sec \theta=1In this case, use the left hand side of the identity to simplify.
In this case, use the simplifying strategy by changing all trig functions to sine and cosine by using the following:
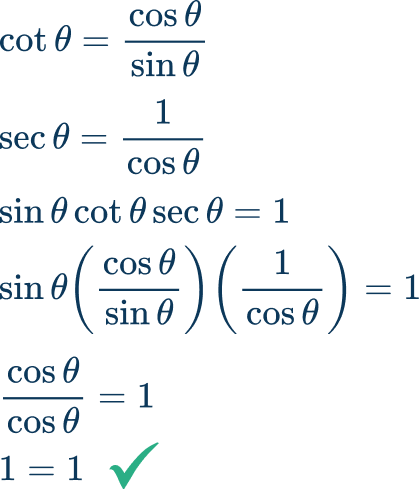
Teaching tips for trigonometry
- Have students investigate trig identities using inquiry based platforms such as Desmos.
- Instead of having students practice problems with worksheets, have them engage in collaborative learning activities such as jigsaw tasks, scavenger hunts, and/or gallery walks.
- Engage students with team game-playing to review skills with platforms such as Blooket and Quizziz.
Easy mistakes to make
- Labeling a triangle incorrectly
For example, this triangle has been incorrectly labeled with the side next to the angle.
The correct way to label it is to name the side across from the angle.
- Mixing up the opposite side and the adjacent side when using SOHCAHTOA
For example, when labeling the sides of the right triangle, be sure to do it with respect to a specific acute angle.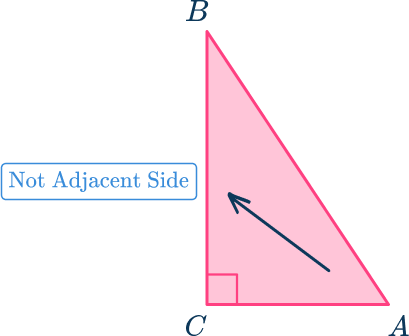
From angle A, the side across from it, is the opposite side.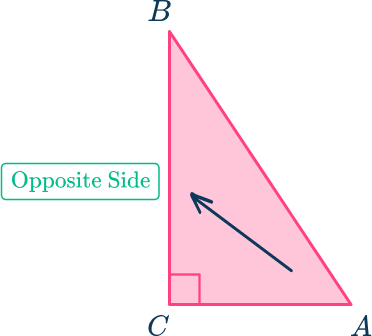
The side that is part of angle A is the adjacent side.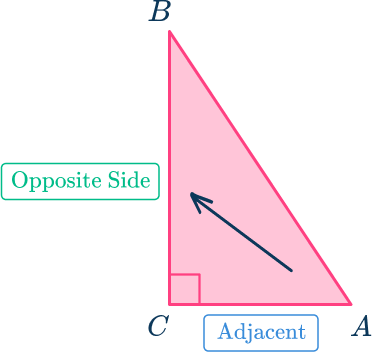
- Rounding the decimal too early
This can lose accuracy marks. Always use as many decimal places as possible throughout the calculation, then round your solution only.
- Using the sine rule instead of cosine rule
Notice the information that is first given with a triangle to determine which rule to use. When you are given SSA, \, AAS, or ASA values, the law of sines is used. When you are given SSS or SAS values, use the law of cosines.
- Not using the included angle
For the cosine rule and the area of a triangle using A=\cfrac{1}{2} \, a b \operatorname{Sin} C, the angle is included between the two sides. Using any other angle will result in an incorrect solution.
- Not using the inverse trig function
For example when solving for angle A, using the sine function instead of the inverse sine.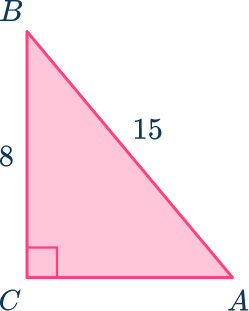
\operatorname{Sin} A=\cfrac{8}{15}
A≠ \sin \cfrac{8}{15}
Instead it should be:
A=\sin ^{-1}\left(\cfrac{8}{15}\right)
Practice trigonometry questions
1. Calculate the length of the hypotenuse.
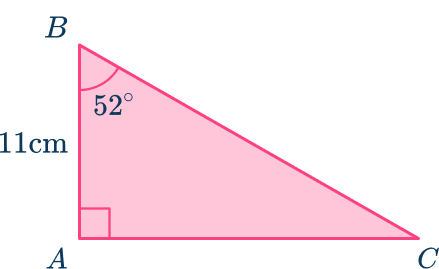




Use SOHCAHTOA to find the missing side length. Label the sides with respect to angle B.
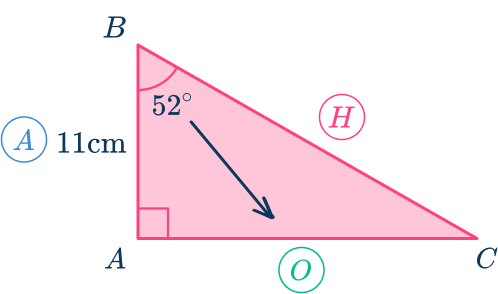
Use the cosine ratio since you have the adjacent side length and need to find the hypotenuse length.
\begin{aligned}& \cos \theta=\cfrac{\text { adjacent }}{\text { hypotenuse }} \\\\ & \cos 52=\cfrac{11}{H} \\\\ & H=\cfrac{11}{\cos (52)} \\\\ & H=17.87 \mathrm{~cm}\end{aligned}
2. Using your knowledge of exact trigonometric values, to find the value of \theta.





Use SOHCAHTOA to find the missing angle. Label the sides with respect to \theta .

Since you have the value of the opposite side and the adjacent side, use the tangent ratio.
\begin{aligned}\tan (\theta) & =\cfrac{\text { Opposite }}{\text { Adjacent }} \\\\ \tan (\theta) & =\cfrac{\sqrt{3}}{1} \\\\ \tan (\theta) & =\sqrt{3} \end{aligned}
Using the exact trigonometric values,
\tan (\theta)=\sqrt{3} when \theta=60^{\circ} \text {.}
3. Find angle \theta.
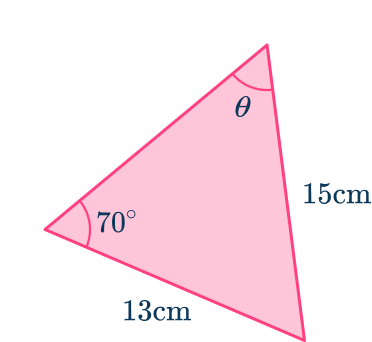




Since it is not a right triangle, you have to use either the law of sines or the law of cosines.
The values given are in a SSA set up, so you can use the law of sines.
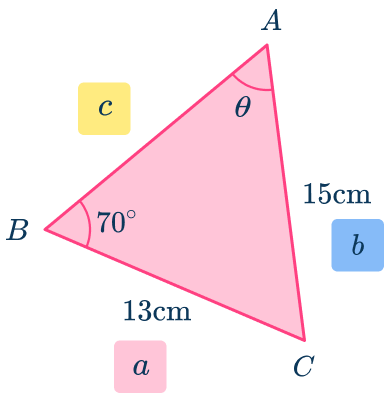
\begin{aligned}\cfrac{\sin(A)}{a}&=\cfrac{\sin(B)}{b} \\\\ \cfrac{\sin(\theta)}{13}&=\cfrac{sin(70)}{15} \\\\ \sin(\theta)&= \cfrac{sin(70)}{15} \times 13 \\\\ \sin(\theta)&=0.8144002713 \\\\ \theta &=\sin^{-1}(0.8144002713) \\\\ \theta&=54.53^{\circ}\end{aligned}
4. Calculate the area of the following triangle:
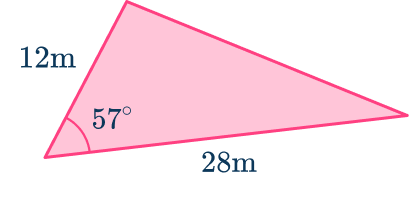




Using trigonometry, find the area of the triangle using,
A=\cfrac{1}{2} \, ab \sin(C)
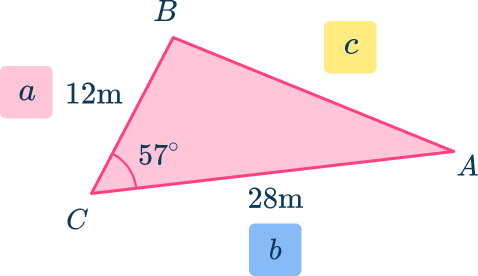
\begin{aligned}A&=\cfrac{1}{2} \times 12 \times 28 \times \sin(57) \\\\ A&= 140.90 \mathrm{~cm}^{2} \end{aligned}
5. Find the exact value of \cos 240^{\circ}.




240^{\circ} is in the third quadrant. The cosine value is always negative in the third quadrant.
To find the reference angle of an angle in the third quadrant, subtract 180 from the original angle.
240-180=60
The reference angle is 60^{\circ}.
\cos 60=\cfrac{1}{2}
So, since the cosine is negative in the third quadrant, \cos 240=- \, \cfrac{1}{2}.
6. Find the exact value of \csc 120^{\circ}.




120^{\circ} is an angle in the second quadrant. The csc is the reciprocal of the sin so it has a positive value in the second quadrant.
To find the reference angle in the second quadrant, subtract the original angle from 180.
180-120=60
The reference angle is 60^{\circ}.
\csc 60=\cfrac{2}{\sqrt{3}} which simplifies to be \cfrac{2 \sqrt{3}}{3}
Since the csc is positive in the second quadrant, \csc 120=\cfrac{2 \sqrt{3}}{3}.
Trigonometry FAQs
Radians are a unit of measure of an angle.
The angle of elevation is an angle that rises up from the horizontal line.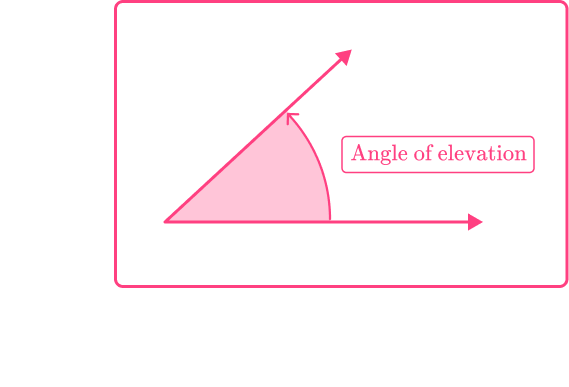
The next lessons are
- Circle math
- Angles of a circle
- Circle theorems
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!