High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Parts of a circle Area of a circle Circumference of a circle

Math resources Geometry

Sectors arcs and segments of a circle

Sectors, arcs and segments of a circle

Here you will learn about sectors, arcs, and segments of a circle including how to identify them, their properties, and how to use them to solve problems involving angles and arcs of circles.

Students will first learn about circle math in the geometry standards in middle school and build upon that knowledge as they progress into a geometry course in high school.

What are sectors, arcs and segments of a circle?

Sectors, arcs and segments of a circle are essential parts of a circle that are formed by chords or radii of a circle. They have specific properties and unique relationships that are used to solve problems.

[FREE] Angles Check for Understanding Quiz (Grade 4)

Teaching sectors, arcs and segments of a circle? Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Angles Check for Understanding Quiz (Grade 4)

DOWNLOAD FREE

Segment of a circle

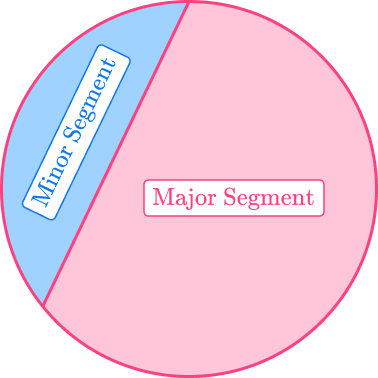
A segment of a circle is the area bounded by a chord of a circle and the area of the circle between the two endpoints of the chord. It is essentially a portion of the circle cut by a chord.

There are two main types of segment:

Major segment: Creates a segment where the arc length is greater than half the circumference of the circle.
Minor segment: Creates a segment where the arc length is less than half the circumference of the circle.

Sectors, Arcs and Segments of a circle 1 US

You can calculate the area of segments of circles.

For example, calculate the area of the segment formed by chord $AB$ of circle $C$ to the nearest tenth.

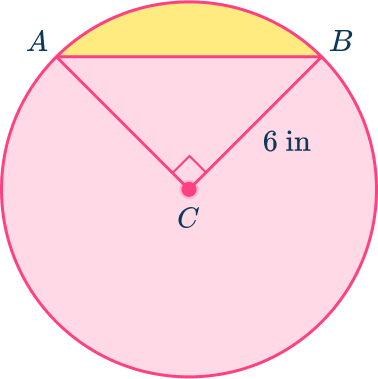
Sectors, Arcs and Segments of a circle 2 US

To calculate the area of the segment, find the area of the entire sector $($ sector formed by radii $AC$ and $BC)$ and subtract the area of the triangle $($ right triangle $ACB).$

Area of a sector: $\cfrac{m A R C}{360} \times \Pi \times r^2$

Note: $\cfrac{m A R C}{360}$ means the degree measurement of the arc in degree (which is the same as the central angle) divided by the complete degree of a circle, $360^{\circ}.$

In this case, the measure of the central angle $($ angle $ACB)$ is $90^{\circ}$ and the radius of the circle is $6$ inches.

Area of a sector $=\cfrac{90}{360}\times\Pi\times(6)^2=\cfrac{1}{4}\times\Pi\times{36}=9\Pi\approx{28.3}\mathrm{~in}^2$

Area of triangle: $\cfrac{1}{2}\times{b}\times{h}=\cfrac{1}{2}\times{6}\times{6}=18\mathrm{~in}^2$

As the area of a segment $=$ Area of a sector – Area of a triangle, the area of the segment is:

28.3-18=10.3\mathrm{~in}^2

Step-by-step guide: Segment of circle

Step-by-step guide: Area of sector

Step-by-step guide: Area of a segment of a circle

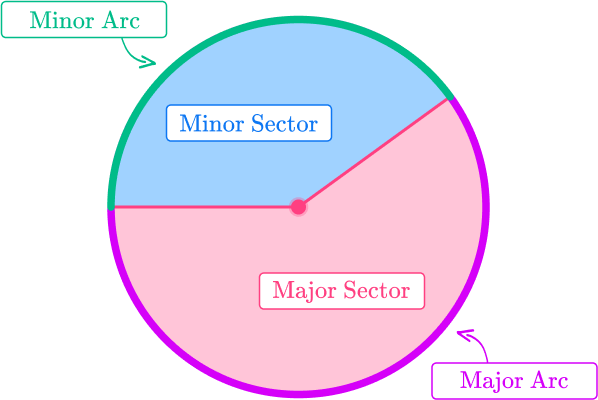
Arc of circle

The arc of a circle is a portion of the edge of the circle or portion of the circumference. Similarly to segments of a circle, you can classify arcs into two different categories.

Major arc: Arcs that are more than half the circumference of the circle.
Minor arcs: Arcs that are less than half the circumference of the circle.

Sectors, Arcs and Segments of a circle 3 US

Like segments of a circle, you can calculate the lengths of arcs as a fraction of the circumference.

For example, calculate the length of minor arc $FG$ in circle $M$ to the nearest tenth.

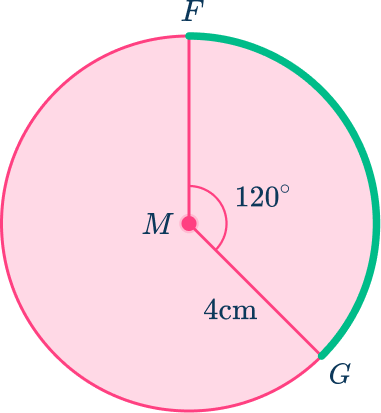
Sectors, Arcs and Segments of a circle 4 US

In circle $M,$ the central angle that intercepts or subtends minor arc $FG$ is $120^{\circ}$ and the radius length is $4 \, cm.$ To calculate the minor arc you can use the formula:

Arc length: $\cfrac{m \operatorname{Arc}}{360} \times 2 \times r \times \Pi=\cfrac{120}{360} \times 2 \times 4 \times \Pi=\cfrac{1}{3} \times 8 \times \Pi=8.4 \mathrm{~cm}$

Step-by-step guide: Arc of a circle

Step-by-step guide: Arc length formula

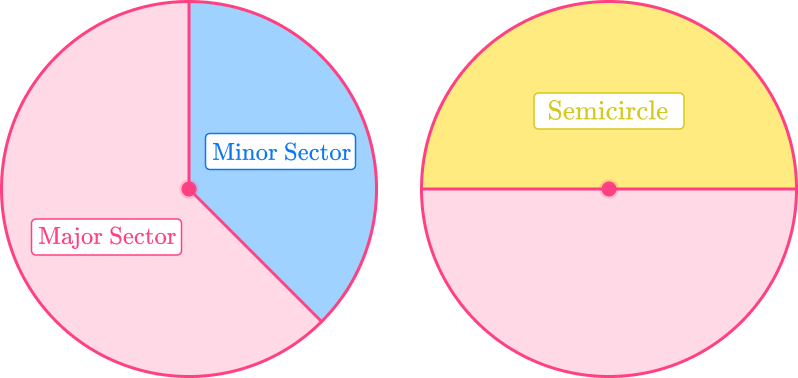
Sectors of circles

A sector of a circle is a portion of a circle created by the arc of the circle and two radii. It is like a piece of pie.

Similar to segments and arcs, sectors of circles can be classified into three categories.

Minor sector: A sector that is less than half the circle.
Major sector: A sector that is greater than half the circle.
Semi-circle: A sector that is equal to half the circle.

Sectors, Arcs and Segments of a circle 5 US

You can calculate the perimeter of a sector and the area of a sector. For example, in circle $X,$ find the perimeter and the area of sector $ZXY.$

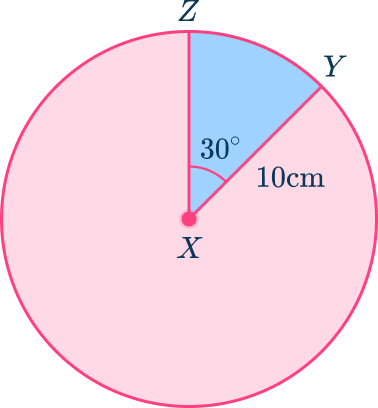
Sectors, Arcs and Segments of a circle 6 US

To calculate the length of the minor sector $ZXY$ , first find the length of minor arc $YZ$ and then add the radii lengths. In this case, the central angle is $30^{\circ}$ and the radii lengths are $10 \, cm.$

Arc length $(YZ)= \cfrac{m A R C}{360} \times 2 \times r \times \Pi=\cfrac{30}{360} \times 2 \times 10 \times \Pi=\cfrac{1}{12} \times 20 \times \Pi=5.2 \mathrm{~cm}$

Perimeter of minor sector $ZXY\text{:}$ radius + radius + arc length $=10+10+5.2=25.2\mathrm{~cm}$

To calculate the area of minor sector $ZXY$ to the nearest tenth, use the formula:

Area of sector: $\cfrac{m A R C}{360} \times \Pi \times r^2=\cfrac{30}{360} \times \Pi \times(10)^2=\cfrac{1}{12} \times \Pi \times 100=26.2 \mathrm{~cm}^2$

Step-by-step-guide: Sector of circle

Step-by-step-guide: Perimeter of a sector

Step-by-step-guide: Area of a sector

What are sectors, arcs and segments of a circle?

Common Core State Standards

How does this relate to high school math?

High School – Geometry – Circles (HS.G.C.B.5)
Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector.

High School: Geometry (HS.G.CO.A.1)
Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc.

How to answer questions on sectors, arcs, and segments of circles

There are a lot of ways to use sectors, arcs, and segments of circles. For more specific step-by-step guides, check out the individual pages linked in the “what are sectors, arcs, and segments of circles?” section or read through the examples below.

In order to solve problems involving sectors, arcs, and segments:

Recall the formula.
Make the calculation or provide an explanation.

Sectors, arcs, and segments of circles examples

Example 1: calculate the area of minor segment

Calculate the area of the segment pictured below to the nearest tenth.

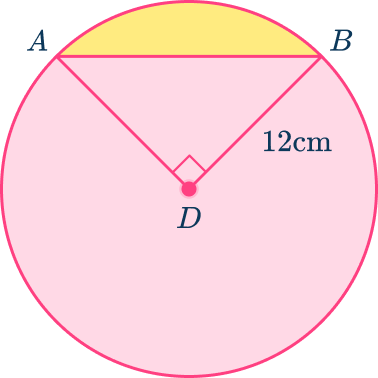
Sectors, Arcs and Segments of a circle 7 US

Recall the formula.

To find the area of a segment, find the area of the sector and then subtract the area of the triangle.

In this case, the central angle that intercepts minor arc $AB$ is $90^{\circ}$ , and the radius length is $12\mathrm{~cm}.$

2Make the calculation or provide an explanation.

Area of sector:

\begin{aligned}&=\cfrac{m A R C}{360} \times \Pi \times r^2 \\\\ &=\cfrac{90}{360} \times \Pi \times 12^2 \\\\ &=\cfrac{1}{4} \times \Pi \times 144 \\\\ &=113.1 \mathrm{~cm}^2 \end{aligned}

To find the area of triangle $ADB$ use: $\cfrac{1}{2} \times b \times h$

Area of triangle $ADB\text{:}$

\cfrac{1}{2} \times 12 \times 12=72 \mathrm{~cm}^2

Area of segment $=$ Area of sector $-$ Area of triangle

Area of segment $=113.1-72=41.1\mathrm{~cm}^2$

Example 2: calculate the area of major sector

Find the area of the major sector pictured below to the nearest tenth.

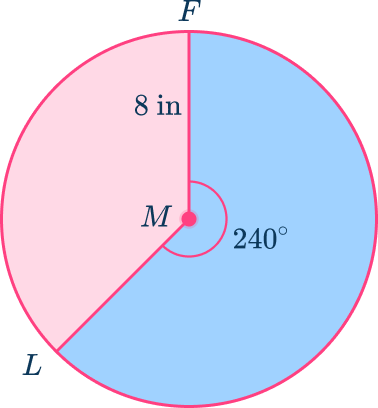
Sectors, Arcs and Segments of a circle 8 US

Recall the formula.

To find the area of a sector, use the formula, $\cfrac{m A R C}{360} \times \Pi \times r^2$

In this case, radius is $8$ inches and the central angle is $240^{\circ}.$

Make the calculation or provide an explanation.

Area of sector:

$\begin{aligned}&=\cfrac{m A R C}{360} \times \Pi \times r^2 \\\\ &=\cfrac{240}{360} \times \Pi \times(8)^2 \\\\ &=\cfrac{2}{3} \times \Pi \times(64) \\\\ &=134.0 \mathrm{~in}^2 \end{aligned}$

Example 3: calculating sector

Find the area of minor sector that has a central angle of $30^{\circ}.$

Leave your answer in terms of pi.

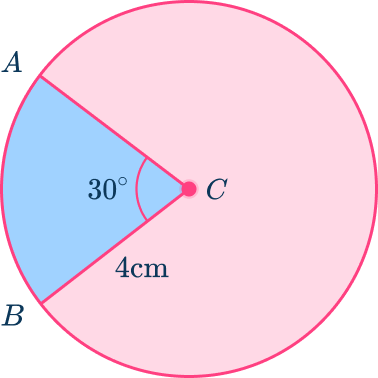
Sectors, Arcs and Segments of a circle 9 US

Recall the formula.

To find the area of a sector, use the formula, $\cfrac{m A R C}{360} \times \Pi \times r^2$

In this case, radius is $4\mathrm{~cm}$ and the central angle is $30^{\circ}.$

Make the calculation or provide an explanation.

Area of sector:

$\begin{aligned}&=\cfrac{m A R C}{360} \times \Pi \times r^2 \\\\ &=\cfrac{30}{360} \times \Pi \times(4)^2 \\\\ &=\cfrac{1}{12} \times \Pi \times(16) \\\\ &= \cfrac{16}{12} \Pi \\\\ &=\cfrac{4}{3} \Pi \mathrm{~cm}^2 \end{aligned}$

Example 4: arc length

Find the length of minor arc $GH$ to the nearest tenth.

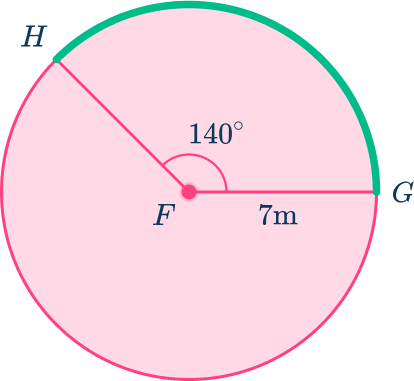
Sectors, Arcs and Segments of a circle 10 US

Recall the formula.

To find the arc length of minor arc $GH,$ use the formula, $\cfrac{\text { mARC }}{360} \times 2 \times r \times \Pi$

In this case, radius is $7\mathrm{~m}$ and the central angle is $140^{\circ}.$

Make the calculation or provide an explanation.

Arc length:

$\begin{aligned}&=\cfrac{m A R C}{360} \times 2 \times r \times \Pi \\\\ &=\cfrac{140}{360} \times 2 \times 7 \times \Pi \\\\ &=\cfrac{140}{360} \times 14 \times \Pi \\\\ &=17.1\mathrm{~m} \end{aligned}$

The length of minor arc $GH$ is $17.1\mathrm{~m}.$

Example 5: arc length

The measure of the angle at the center of the circle $M$ is $50$ degrees.

Find the length of the major arc $DL$ to the nearest tenth.

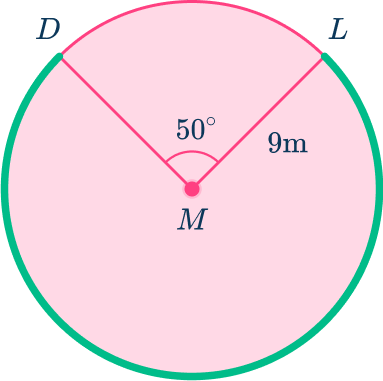
Sectors, Arcs and Segments of a circle 11 US

Recall the formula.

To find the arc length of major arc $DL,$ use the formula, $\cfrac{\text { mARC }}{360} \times 2 \times r \times \Pi.$

In this case, radius is $9\mathrm{~m}$ and the central angle is $50^{\circ}.$

Make the calculation or provide an explanation.

Arc length:

$\begin{aligned}&=\cfrac{m A R C}{360} \times 2 \times r \times \Pi \\\\ &=\cfrac{50}{360} \times 2 \times 9 \times \Pi \\\\ &=\cfrac{50}{360} \times 18 \times \Pi \\\\ &=7.9\mathrm{~m} \end{aligned}$

The length of major arc $DL$ is $7.9\mathrm{~m}.$

Example 6: arc length

The arc length of a minor arc of a circle with a central angle of $60^{\circ}$ is $8\Pi\mathrm{~inches},$ find the radius of the circle.

Recall the formula.

When working with arc length, the formula to use is:

Arc Length $=\cfrac{m A R C}{360} \times 2 \times r \times \Pi$

In this case, the arc length is $8\Pi$ and the central angle is $60^{\circ}.$ Substitute those values into the equation to find the radius length.

Make the calculation or provide an explanation.

Arc Length $=\cfrac{\operatorname{mARC}}{360} \times 2 \times r \times \Pi$

$\begin{aligned}8 \Pi&=\cfrac{60}{360} \times 2 \times r \times \Pi \\\\ 8&=\cfrac{1}{6} \times 2 \times r \\\\ 4&=\cfrac{1}{6} \times r \\\\ 24&=r \end{aligned}$

The radius of the circle is $24$ inches.

Teaching tips for sectors, arcs and segments

Instead of relying on worksheets for students to practice skills, consider interactive activities for student practice. Provide students with real-world examples so the concepts are relevant to them.

Use technology to allow students to interact with circles in a different way. There are many educational apps and interactive websites that offer simulations and exercises that focus on problem solving and lead to deeper understanding.

Use investigative type activities so that students can explore circle math concepts.

Easy mistakes to make

Confusing the sector and segment of a circle
The sector of a circle is a portion of the area of the circle whereas a segment is part of a sector minus the triangle. You can relate it to pizza, a sector is like a piece of pizza and a segment is like the crust of the pizza.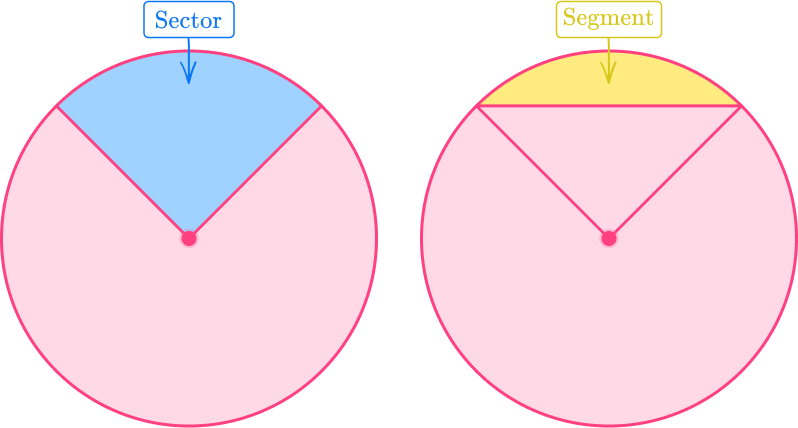

Using the diameter instead of radius to calculate the area of a sector or finding the area of a segment
Like when you find the area of a circle, it is the radius dimension that is needed to calculate not the diameter. If you are given the diameter length, divide it by $2$ to find the radius length.

Thinking the arc length is a squared dimension
The arc length of a circle is part of the circumference, so it is a one dimensional measurement, not a square dimension like area.

Sectors, arcs, and segments practice problems

2.6 \mathrm{~cm}^2

3.9 \mathrm{~cm}^2

5.2 \mathrm{~cm}^2

5.7 \mathrm{~cm}^2

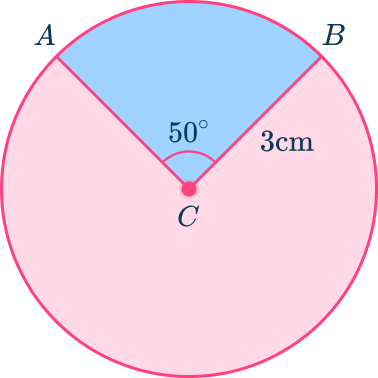
To find the area of a sector use the formula, $\cfrac{m A R C}{360} \times \Pi \times r^2.$

In this case substitute $3$ for the radius and $50^{\circ}$ for the arc measurement.

\begin{aligned}\text { Area of sector }&=\cfrac{50}{360} \times \Pi \times 3^2 \\\\ &=\cfrac{5}{36} \times \Pi \times 9 \\\\ &\approx 3.9 \mathrm{~cm}^2 \end{aligned}

5.7\mathrm{~cm}

5.2\mathrm{~cm}

3.9\mathrm{~cm}

2.6\mathrm{~cm}

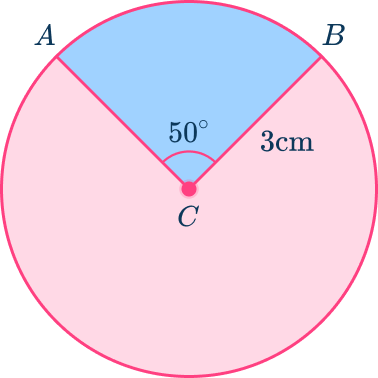
To find the arc length of minor arc $AB,$ use the formula,

Arc Length $=\cfrac{m A R C}{360} \times 2 \times r \times \Pi$

In this case, substitute in $3$ for the radius and $50^{\circ}$ for the arc measurement.

\begin{aligned}\text { Arc Length }&=\cfrac{50}{360} \times 2 \times 3 \times \Pi \\\\ &=\cfrac{5}{36} \times 6 \times \Pi \\\\ &\approx 2.6 \mathrm{~cm} \end{aligned}

5\mathrm{~in}

10\mathrm{~in}

6\mathrm{~in}

12\mathrm{~in}

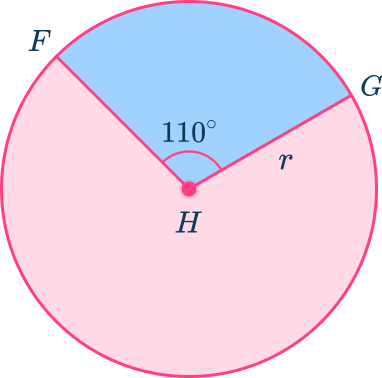
Using the formula, Arc Length $=\cfrac{\operatorname{mARC}}{360} \times 2 \times r \times \Pi,$ substitute in the value $110^{\circ}$ for the arc measurement and $9.6$ for the arc length in order to solve for $r.$

\begin{aligned}\text { Arc Length }&=\cfrac{m A R C}{360} \times 2 \times r \times \Pi \\\\ 9.6&=\cfrac{110}{360} \times 2 \times r \times \Pi \\\\ 4.8&=\cfrac{11}{36} \times r \times \Pi \\\\ 5.00&=r \end{aligned}

The radius is $5\mathrm{~inches}.$ As the diameter is twice that length, the diameter of the circle is $10\mathrm{~inches}.$

32\mathrm{~m}^2

50.3 \mathrm{~m}^2

18.3 \mathrm{~m}^2

100.5 \mathrm{~m}^2

To find the area of a segment of a circle, find the area of the sector and subtract away the area of the triangle.

In this case the sector has a central angle of $90^{\circ}$ and radius length of $8 \, m.$

Use that information to find the area of the sector using the formula, $\cfrac{m A R C}{360} \times \Pi \times r^2.$

\begin{aligned}\text { Area of sector }&=\cfrac{90}{360} \times \Pi \times(8)^2 \\\\ &=\cfrac{1}{4} \times \Pi \times 64\\\\&=50.3 \mathrm{~m}^2 \end{aligned}

The area of the triangle is $\cfrac{1}{2} \times b \times h$ where the base and the height of triangle $GSH$ is $8$ meters.

Use that value to find the area of the triangle.

\begin{aligned}\text { Area of triangle }&=\cfrac{1}{2} \times 8 \times 8 \\\\ &=\cfrac{1}{2} \times 64 \\\\ &=32 \mathrm{~m}^2 \end{aligned}

To find the area of the segment of the circle, subtract the two areas.

\text { Area of segment }=50.3-32=18.3 \mathrm{~m}^2.

17.8 \mathrm{~in}^2

22.3 \mathrm{~in}^2

4.5 \mathrm{~in}^2

35.6 \mathrm{~in}^2

To find the area of a segment of a circle, find the area of the sector and subtract the area of the triangle.

In this case the circle has a radius of $4\mathrm{~in}$ and the central angle of the sector is $160^{\circ}.$ Use those values to find the area of the sector.

\begin{aligned}\text { Area of sector }&=\cfrac{\operatorname{mARC}}{360} \times \Pi \times r^2 \\\\ &=\cfrac{160}{360} \times \Pi \times(4)^2 \\\\ &=\cfrac{4}{9} \times \Pi \times 16 \\\\ &=22.3 \mathrm{~in}^2 \end{aligned}

Next, find the area of triangle $ABC$ which has a base of $AC$ and perpendicular height $BD ($ the angle $ADB$ is a right angle $).$

\begin{aligned}\text { Area of triangle }&=\cfrac{1}{2} \times 1.5 \times 6 \\\\ &=3 \times 1.5 \\\\ &=4.5 \mathrm{~in}^2 \end{aligned}

\begin{aligned}\text { Area of segment }&=\text { Area of sector }- \text { Area of triangle } \\\\ &=22.3-4.5 \\\\ &=17.8 \mathrm{~in}^2 \end{aligned}

3\mathrm{~cm}

6\mathrm{~cm}

9\mathrm{~cm}

12\mathrm{~cm}

In this case, use the formula for the area of a sector,

\text { Area of sector }=\cfrac{m A R C}{360} \times \Pi \times r^2

Substitute the given information into the formula, the inscribed angle $240^{\circ}$ for the measure of the arc and $6\Pi$ for the area of the sector.

\begin{aligned}6\Pi&=\cfrac{240}{360} \times \Pi \times r^2 \\\\ 6&=\cfrac{2}{3} \times r^2 \\\\ 9&=r^2 \\\\ 3&=r \end{aligned}

The radius of the circle is $3\mathrm{~cm}.$

Sectors, arcs and segments of a circle FAQs

Is the arc length the same as the degree measurement of the arc?

No, the arc length is part of the circumference which is the distance around a circle.

The measurement of the arc in degrees represents the fractional part of the complete degree of a circle which is $360^{\circ}.$

So, the measurement of an arc will be less than $360^{\circ}.$

Is the measurement of the central angle of a circle or the arc always in degrees?

No, there are times you will be given the arc measurement or the central angle measurement in radians instead of degrees.

If you are given the central angle in radians, the formula to use to find arc length is $s=\Theta \times r$ and to find the area of the sector when given the angle in radians is $A=\cfrac{\Theta}{2} r^2.$

In a precalculus class, radian measures are more often given than degree measurements.

What if the triangle used to find the area of the segment is not a right triangle, how can you find the area of it?

If the triangle is not a right triangle, you will be given enough information to find the height and the base to calculate the area.

For example, you can use trigonometry to find missing dimensions.

How do you find the central angle of a circle if you know the angle at the circumference, inscribed by the same two vertices?

The angle at the center of a circle is twice the measure of the angle at the circumference of the circle subtended by the same two vertex points that lie on the circumference.

The measure of an angle inside a circle can be determined using circle theorems, such as the inscribed angle theorem.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.