Perimeter of a Sector

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Parts of a circle Circumference of a circle Arc of a circle Solving equations Law of cosines Rounding

Math resources Geometry

Angles of a circle

Perimeter of a sector

Here you will learn about the perimeter of a sector of a circle including how to find the perimeter of a sector with a given angle and radius, and how to find the radius of a circle when given the perimeter of the sector.

Students will first learn about the perimeter of a sector as part of geometry in high school.

What is the perimeter of a sector?

The perimeter of a sector is the distance around a sector of a circle.

A sector of a circle is the area enclosed by two radii and the arc between them.

You can calculate the perimeter of a sector by adding together the lengths of the two radii and the arc length of the sector.

For example,

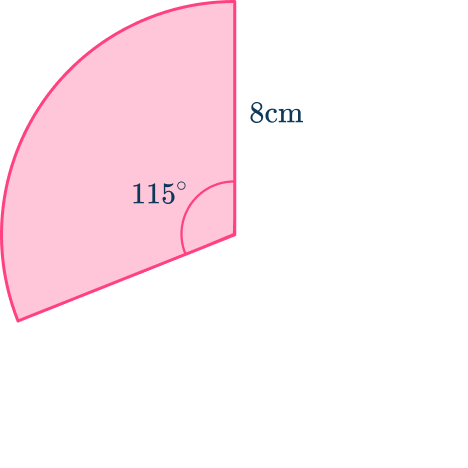
Calculate the perimeter of this sector to the nearest tenth.

[FREE] Perimeter Check for Understanding Quiz (Grade 3 and 4)

Use this quiz to check your grade 3 and 4 students’ understanding of perimeter. 10+ questions with answers covering a range of 3rd and 4th grade perimeter topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Perimeter Check for Understanding Quiz (Grade 3 and 4)

DOWNLOAD FREE

Arc length formula

$\text { Arc length } = \cfrac{\theta}{360} \times \pi \times d$

$\theta$ – Angle of the sector

$r$ – Radius of the circle

$\text { Arc length } = \cfrac{\theta}{360} \times 2\times\pi \times r$

$\theta$ – Angle of the sector

$r$ – Radius of the circle

Here angle $\theta = 115^{\circ}$ and $r = 8,$ so

$\begin{aligned} \text { Arc length }&=\cfrac{115}{360} \times 2 \times \pi \times 8 \\\\ &=16.05702912 \ldots \\\\ \end{aligned}$

To calculate the perimeter of the sector, you need to add the arc length to the lengths of the two radii.

Perimeter of a sector formula

Perimeter of a sector $=$ Arc length $+$ radius $+$ radius

$\begin{aligned} &=16.05702912 + 8 + 8\\\\ &=32.05702912\ldots\\\\ &=32.1cm \; \text{(nearest tenth)} \end{aligned}$

What is the perimeter of a sector?

Common Core State Standards

How does this relate to high school math?

High School – Geometry – Circles (HS.G.C.B.5)
Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector.

How to find the perimeter of a sector

In order to find the perimeter of a sector:

Find the length of the diameter/radius.
Find the size of the angle creating the arc of the sector.
Find the arc length of the sector.
Add together the arc length and the two radii.
Clearly state your answer.

Perimeter of a sector examples

Example 1: calculate the perimeter of a sector (quadrant)

Calculate the perimeter of the sector.

Give your answer to the nearest thousandth.

Find the length of the diameter/radius.

Radius = $6{~cm}$

2Find the size of the angle creating the arc of the sector.

This is the central angle of the circle (the angle at the center of the circle).

Angle = $90^{\circ}.$ Shown by the symbol of the right angle

3Find the arc length of the sector.

\begin{aligned} \text {Arc length} &= \cfrac{\theta}{360} \times 2\times\pi \times r \\\\ &=\cfrac{\theta}{360} \times 2\times\pi \times r \\\\ &=\cfrac{90}{360} \times 2\times\pi \times 6 \\\\ &=3\pi \end{aligned}

4Add together the arc length and the two radii.

Arc length: $3 \pi{~cm}$

Radius: $6{~cm}$

\text {Total perimeter of sector} = 3\pi + 6 + 6{~cm}

\text {Total perimeter of sector} = 3\pi + 12{~cm}

5Clearly state your answer.

The question asked you to round your answer to the nearest thousandth.

\text {Perimeter of sector} = 3\pi + 12{~cm}

\text {Arc length} =21.424777..{~cm}

\text {Arc length} =21.425{~cm}

Remember, the perimeter of a sector is a measure of distance, and therefore the units are not squared.

Example 2: calculate the perimeter of a sector (semi circle)

Calculate the perimeter of the semicircle shown below.

Give your answer in terms of $\pi.$

Find the length of the diameter/radius.

Diameter = $24{~cm}$

Find the size of the angle creating the arc of the sector.

Angle = $180^{\circ}.$ This is because the shape shown is a semi circle. Therefore the angle of the straight line is $180$ degrees.

Find the arc length of the sector.

\begin{aligned} \text {Arc length} &= \cfrac{\theta}{360} \times \pi\times d \\\\ &=\cfrac{\theta}{360} \times \pi\times d \\\\ &=\cfrac{180}{360} \times \pi\times 24 \\\\ &=12\pi \end{aligned}

Add together the arc length and the two radii.

Arc Length: $12\pi{~cm}$

Diameter: $24{~cm}$

Radius: $12{~cm}$

$\text {Total perimeter of sector} = 12\pi + 12 +12{~cm}$

$\text {Total perimeter of sector} = 12\pi + 24{~cm}$

Clearly state your answer.

The question asks you to give your answer in terms of $\pi.$

$\text {Perimeter of sector} = 12\pi + 24{~cm}$

This answer is in terms of $\pi.$

Example 3: calculate the perimeter of a sector (with an angle given)

Calculate the perimeter of the sector shown below.

Give your answer to $3$ significant figures.

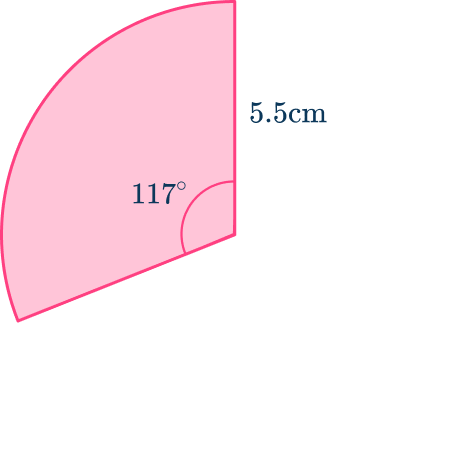
Find the length of the diameter/radius.

Radius = $5.5{~cm}$

Find the size of the angle creating the arc of the sector.

Angle= $117^{\circ}$

Find the arc length of the sector.

\begin{aligned} \text {Arc length} &= \cfrac{\theta}{360} \times 2\times\pi \times r \\\\ &=\cfrac{\theta}{360} \times 2\times\pi \times r \\\\ &=\cfrac{117}{360} \times 2\times\pi \times 5.5 \\\\ &=\cfrac{143}{40} \pi \end{aligned}

Add together the arc length and the two radii.

Arc length: $\cfrac{143}{40} \pi$

Radius: $5.5{~cm}$

$\text {Total perimeter of sector} = \cfrac{143}{40} \pi + 5.5 +5.5{~cm}$

$\text {Total perimeter of sector} = \cfrac{143}{40} \pi + 11{~cm}$

Clearly state your answer.

The question asked you to round your answer to $3$ significant figures.

$\text {Perimeter of a sector} = \cfrac{143}{40} \pi + 11{~cm}$

$\text {Perimeter of a sector} = 22.2311…{~cm}$

$\text {Perimeter of a sector} = 22.2{~cm}$

Example 4: calculate the perimeter of a sector (the angle is not given)

Calculate the perimeter of the sector $AOB$ below.

The length of the radius $(OB)$ is $19{~cm}.$

The length of a chord $(AB)$ is $10{~cm}.$

Give your answer to the nearest tenth.

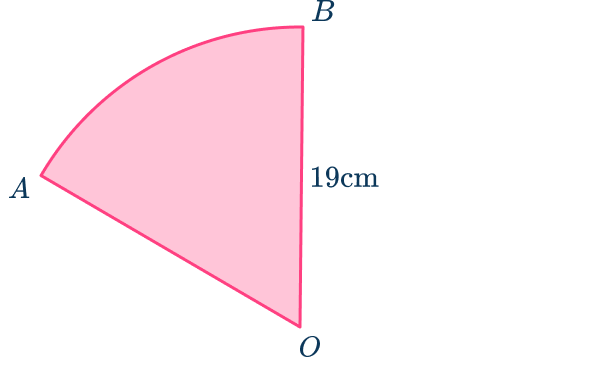
Find the length of the diameter/radius.

Radius = $19{~cm}$

Find the size of the angle creating the arc of the sector.

In this example, you are not given the angle of the sector; you need to calculate it first.

Here you can use the triangle created by the two radii and the chord to find the angle. (see below)

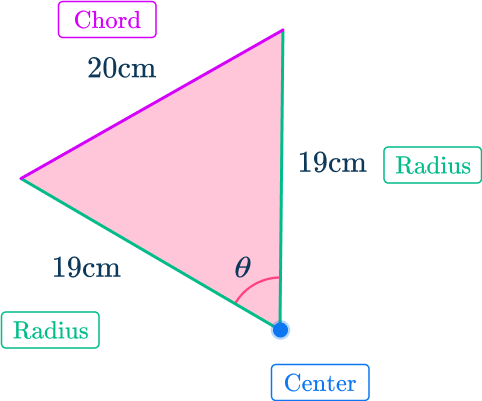
You will need to use the cosine rule to find the angle.

$a^2=b^2+c^2-2bcCos(A)$

$A$ is the angle you are trying to find. You can therefore use the rearranged cosine rule to find the angle.

$\begin{aligned} \operatorname{Cos} A&=\cfrac{b^{2}+c^{2}-a^{2}}{2 b c} \\\\ \operatorname{Cos} A&=\cfrac{19^{2}+19^{2}-20^{2}}{2 \times 19 \times 19} \\\\ \operatorname{Cos} A&=\cfrac{161}{361} \\\\ A&=\operatorname{Cos}^{-1}\left(\cfrac{161}{361}\right) \\\\ A&=63.51^{\circ} \end{aligned}$

The size of the angle creating the sector (made by the two radii) is $63.5^{\circ}.$

Find the arc length of the sector.

As you know the radius you can use the formula which has $‘r’$ as a variable.

$\begin{aligned} \text {Arc length} &= \cfrac{\theta}{360} \times 2\times\pi \times r \\\\ &=\cfrac{\theta}{360} \times 2\times\pi \times r \\\\ &=\cfrac{63.5}{360} \times 2\times\pi \times 19 \\\\ &=21.057\ldots \end{aligned}$

Add together the arc length and the two radii.

Arc length: $21.057{~cm}$

Radius: $19{~cm}$

Notice how you round this to more than the final answers required. This is to avoid rounding errors.

$\text {Total perimeter of sector} = 21.057 + 19 + 19{~cm}$

$\text {Total perimeter of sector} = 59.057{~cm}$

Clearly state your answer.

The question asked you to round your answer to the nearest tenth.

$\text {Arc length} =59.057{~cm}$

$\text {Arc length} =59.1{~cm}$

How to solve problems involving the perimeter of a sector

Sometimes you may be given the perimeter of a sector and asked to find a property of the circle, such as the radius. In this case you need to ‘reverse’ the process.

Clearly state which of the properties you know and do not know.
Create an equation for the perimeter of the sector and substitute in the value you know.
Solve the equation to find the unknown property.
Clearly state your answer.

Solving problems involving perimeter of a sector examples

Example 5: finding the radius given the perimeter of a sector

The sector below has a perimeter of $20{~cm}$ and an angle of $125^{\circ}.$ Calculate the length of $x.$

Give your answer to the nearest hundredth.

Clearly state which of the properties you know and do not know.

Radius – $x$

Angle of sector – $125^{\circ}$

Perimeter of a sector – $20{~cm}$

Arc length – $\cfrac{125}{360} \times 2\times\pi \times x$

Arc length – $\cfrac{25x}{36} \times\pi$

Create an equation for the perimeter of the sector and substitute in the value you know.

\text {Perimeter of sector } = \text{ Arc length } + \text{ radius } + \text{ radius}

$20 = \cfrac{25}{36} \pi x+x+x \hspace{1cm}$ Substitute in values

$20 = \cfrac{25}{36} \pi x+2 x \hspace{1.35cm}$ Simplify $x+x$

Solve the equation to find the unknown property.

$20=\cfrac{25}{36} \pi x + 2x \hspace{1cm}$ Simplify $x + x$

$20=x\left(\cfrac{25}{36} \pi+2\right) \hspace{.6cm}$ Take $x$ out as a factor

$20=x(4.18166)$

$20 \div 4.18166=x \hspace{.9cm}$ Make $x$ the subject

$4.783 \ldots=x$

Clearly state your answer.

The question asks you to give your answer to the nearest hundredth.

$x=4.783\ldots$

$x=4.78$

Example 6: finding the angle of a sector given the perimeter of a sector

The sector below has a perimeter $r$ of $62{~cm}$ and a radius of $18{~cm}.$

Calculate the angle $x.$

Give your answer to the nearest hundredth.

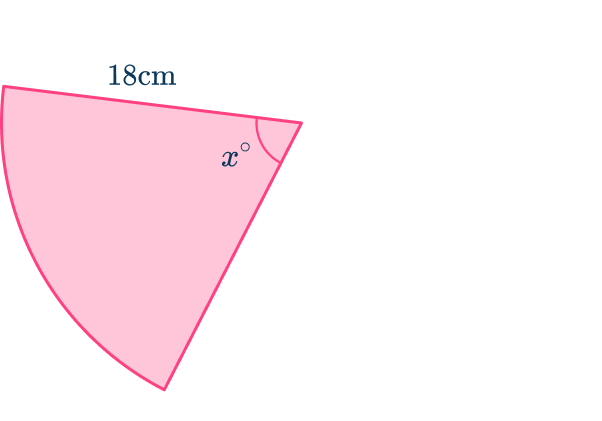
Clearly state which of the properties you know and do not know.

Radius – $18$

Angle of sector – $x^{\circ}$

Perimeter of a sector – $62{~cm}$

Arc length = $\cfrac{x}{360} \times 2 \times \pi \times 18$

Arc length = $\cfrac{1}{10} \pi x$

Create an equation for the perimeter of the sector and substitute in the value you know.

$\text { Perimeter of sector }=\text { Arc length }+\text { radius }+\text { radius }$

$62=\cfrac{1}{10} \pi x+18+18 \hspace{0.8cm}$ Substitute in values

$62=\cfrac{1}{10} \pi x+36 \hspace{1.5cm}$ Simplify

$26=\cfrac{1}{10} \pi x$

Solve the equation to find the unknown property.

26=\cfrac{1}{10} \pi x

$26 \div \cfrac{\pi}{10}=x \hspace{1cm}$ Make $x$ the subject

$82.76057=x$

Clearly state your answer.

The question asks you to give your answer to the nearest hundredth.

$x=82.76057\ldots$

$x=82.76$

Teaching tips for perimeter of a sector

Begin by introducing or reviewing key terms like sector (along with major sector and minor sector), radius, arc, circumference, and central angle. Ensure students understand these terms, as they are essential for grasping the concept of a sector’s perimeter.

Ensure that students understand that a sector is part of the circle, and its perimeter includes the arc length of a sector, which is a fraction of the circumference of the circle. This helps students connect the concept to what they already know about circles.

Include real-life problems on worksheets, like finding the perimeter of a slice of pizza or a pie, to make the idea of a sector and its perimeter more tangible.

If a problem involves a sector where the arc length or a side length is unknown, connect to trigonometry by showing how trigonometric functions (sine, cosine, tangent) can help find missing side lengths or angles. For example, in right triangles formed within a sector, the radius and trigonometric functions can calculate an unknown arc length or angle.

Easy mistakes to make

Finding the length of the arc not the perimeter of the sector
You must remember that the perimeter of the sector is the combined length of the arc and the two radii.

Incorrect units
Remember the perimeter is a length and therefore the units will not be squared or cubed. Square units are for area and cubed units are for volume.

Using incorrect formulas
Using incorrect formulas or mixing up formulas for perimeter, arc length, and area of a sector of a circle, resulting in errors.

Practice perimeter of a sector questions

circumference

sector

arc

minor arc

A sector with an angle of $360^{\circ}$ is a full circle.

Therefore the perimeter of the sector is the whole length of the outside of the circle which is called the circumference.

$2$ radii

The arc only

The arc and one radius

The arc and two radii

The perimeter of a shape is the distance around a two-dimensional shape.

Therefore the perimeter of a sector is the combined length of the arc and two radii.

5\pi + 20{~cm}

5\pi{~cm}

25\pi{~cm^2}

35.7{~cm}

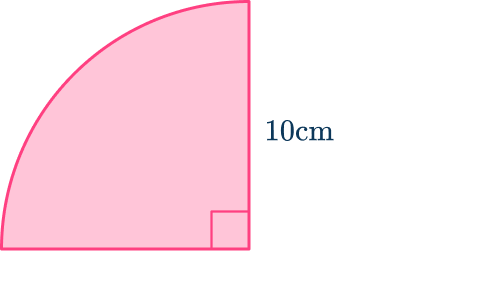
Total perimeter of sector $= \text{ Length of arc } + \text{ radius } + \text{ radius}$

Total perimeter of sector $= 5\pi +10 + 10{~cm}$

Total perimeter of sector $= 5\pi +20{~cm}$

The answer is in terms of pi.

51.4{~cm}

10\pi{~cm}

10\pi+20{~cm^2}

10\pi+20{~cm}

Total perimeter of sector $= \text{ Length of arc } + \text{ radius } + \text{ radius}$

Total perimeter of sector $= 10\pi +10 + 10{~cm}$

Total perimeter of sector $= 10\pi +20{~cm}$

The answer is in terms of pi.

107.4{~cm}

192\pi{~cm^2}

24\pi+32{~cm}

24\pi{~cm}

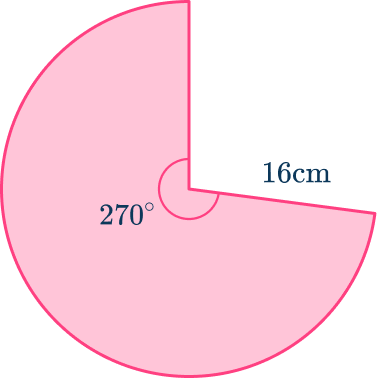
Total perimeter of sector $= \text{ Length of arc } + \text{ radius } + \text{ radius}$

Total perimeter of sector $= 24\pi +16 + 16{~cm}$

Total perimeter of sector $= 24\pi +32{~cm}$

The answer is in terms of pi.

30.0{~cm}

21.99{~cm}

14\pi{~cm^2}

7\pi+8{~cm}

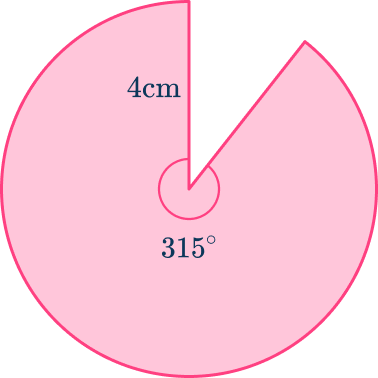
Total perimeter of sector $= \text{ Length of arc } + \text{ radius } + \text{ radius}$

Total perimeter of sector $= 7\pi +4 + 4{~cm}$

Total perimeter of sector $= 7\pi +8{~cm}$

Total perimeter of sector $= 29.9911{~cm}$

Total perimeter of sector $= 30.0{~cm}$

Perimeter of a sector FAQs

What is a sector of a circle?

A sector of a circle is a section of a circle bounded by two radii and the arc between them, resembling a “slice” of the circle.

What is the perimeter of a sector of a circle?

The perimeter of a sector is the total distance around a sector of the circle, which includes the lengths of the two radii and the arc between them.

What is the difference between the perimeter of the sector and the area of the sector?

The perimeter of a sector measures the distance around the edge of the sector, including the arc and the two radii. The area of a sector measures the space enclosed by the sector.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.