Vector Multiplication - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Adding and subtracting integers Adding and subtracting negative numbers

Vectors

Adding vectors Algebraic expression

Math resources Algebra

Vectors

Vector multiplication

Here you will learn about vector multiplication, including scalar multiplication of a vector (multiplication of a vector by a number).

Students will first learn about vector multiplication as part of number and quantity in high school.

What is vector multiplication?

Vector multiplication is when you multiply a vector by a number called a scalar. The scalar has magnitude only, whereas a vector has magnitude and direction.

To do this, you multiply each component of the vector by the scalar.

For example,

Vector $\textbf{a}$ is $\textbf{a} = \begin{pmatrix} \; 2 \; \\ \; 1 \; \end{pmatrix} .$

So multiplying the vector $\textbf{a}$ by $3$ would be

3\textbf{a} = 3 \begin{pmatrix} \; 2 \; \\ \; 1 \; \end{pmatrix} = \begin{pmatrix} \; 3 \times 2 \; \\ \; 3 \times 1 \; \end{pmatrix} = \begin{pmatrix} \; 6 \; \\ \; 3 \; \end{pmatrix}

The image below shows a visual representation of the vectors $\textbf{a}$ and $3\textbf{a}.$

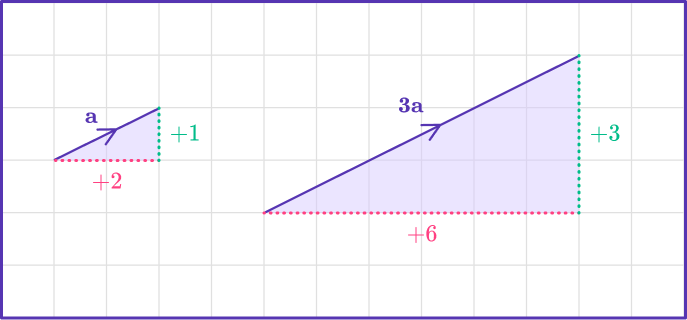
This works because multiplication is repeated addition. Another way of thinking about multiplying the vector $\textbf{a}$ by $3$ would be

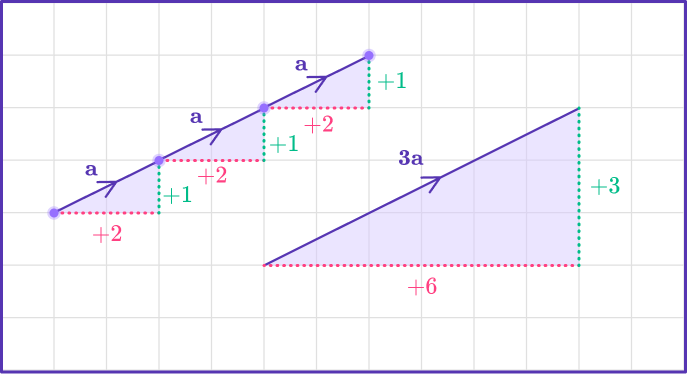
3\textbf{a}=\textbf{a}+\textbf{a}+\textbf{a}= \begin{pmatrix} \; 2 \; \\ \; 1 \; \end{pmatrix} + \begin{pmatrix} \; 2 \; \\ \; 1 \; \end{pmatrix} + \begin{pmatrix} \; 2 \; \\ \; 1 \; \end{pmatrix} = \begin{pmatrix} \; 6 \; \\ \; 3 \; \end{pmatrix}

You can see $3$ groups of the $x$ component and $3$ groups of the $y$ component on the diagram.

When multiplied by a scalar number, the direction of the vector is the same as the original vector, but the magnitude of the vector (also called the absolute value of the vector) has changed.

In general,

$a \begin{pmatrix} \; b \; \\ \; c \; \end{pmatrix} = \begin{pmatrix} \; b \times a \; \\ \; c \times a \; \end{pmatrix} = \begin{pmatrix} \; ab \; \\ \; ac \; \end{pmatrix}$

for any value of $a, \, b,$ and $c.$

What is vector multiplication?

Common Core State Standards

How does this relate to high school math?

High School – Number and Quantity – Vector & Matrix Quantities (HSN.VM.B.5)
Multiply a vector by a scalar.

[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)

Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th and 8th grade algebra topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)

DOWNLOAD FREE

How to multiply a vector by a scalar

In order to multiply a vector by a scalar:

Multiply the $\textbf{x}$ component by the scalar.
Multiply the $\textbf{y}$ component by the scalar.
Write the resultant vector.

Vector multiplication examples

Example 1: vector multiplication

Solve $2 \begin{pmatrix} \; 4 \; \\ \; 5 \; \end{pmatrix}$ .

Multiply the $\textbf{x}$ component by the scalar.

Multiply the scalar number by the top number.

2\times4=8

2Multiply the $\textbf{y}$ component by the scalar.

Multiply the scalar number by the bottom number.

2\times5=10

3Write the resultant vector.

Write the two answers as a column vector.

2 \begin{pmatrix} \; 4 \; \\ \; 5 \; \end{pmatrix} = \begin{pmatrix} \; 2 \times 4 \; \\ \; 2 \times 5 \; \end{pmatrix} = \begin{pmatrix} \; 8 \; \\ \; 10 \; \end{pmatrix}

Example 2: vector multiplication

Solve $4 \begin{pmatrix} \; 8 \; \\ \; 3 \; \end{pmatrix}$ .

Multiply the $\textbf{x}$ component by the scalar.

Multiply the scalar number by the top number.

$4\times8=32$

Multiply the $\textbf{y}$ component by the scalar.

Multiply the scalar number by the bottom number.

$4\times3=12$

Write the resultant vector.

Write the two answers as a column vector.

$4 \begin{pmatrix} \; 8 \; \\ \; 3 \; \end{pmatrix} = \begin{pmatrix} \; 4 \times 8 \; \\ \; 4 \times 3 \; \end{pmatrix} = \begin{pmatrix} \; 32 \; \\ \; 12 \; \end{pmatrix}$

Example 3: vector multiplication, decimal scalar

Solve $0.5 \begin{pmatrix} \; 10 \; \\ \; 8 \; \end{pmatrix}$ .

Multiply the $\textbf{x}$ component by the scalar.

Multiply the scalar number by the top number.

$0.5\times10=5$

Multiply the $\textbf{y}$ component by the scalar.

Multiply the scalar number by the bottom number.

$0.5\times8=4$

Write the resultant vector.

Write the two answers as a column vector.

$0.5 \begin{pmatrix} \; 10 \; \\ \; 8 \; \end{pmatrix} = \begin{pmatrix} \; 0.5 \times 10 \; \\ \; 0.5 \times 8 \; \end{pmatrix} = \begin{pmatrix} \; 5 \; \\ \; 4 \; \end{pmatrix}$

Example 4: vector multiplication, fractional scalar

Solve $\cfrac{1}{3} \begin{pmatrix} \; - \, 6 \; \\ \; 9 \; \end{pmatrix}$ .

Multiply the $\textbf{x}$ component by the scalar.

Multiply the scalar number by the top number.

$\cfrac{1}{3}\times - \, 6=- \, 2$

Multiply the $\textbf{y}$ component by the scalar.

Multiply the scalar number by the bottom number.

$\cfrac{1}{3}\times9=3$

Write the resultant vector.

Write the two answers as a column vector.

$\cfrac{1}{3} \begin{pmatrix} \; - \, 6 \; \\ \; 9 \; \end{pmatrix} = \begin{pmatrix} \; \cfrac{1}{3} \times - \, 6 \; \\ \; \cfrac{1}{3} \times 9 \; \end{pmatrix} = \begin{pmatrix} \; - \, 2 \; \\ \; 3 \; \end{pmatrix}$

Example 5: vector multiplication

Solve $4 \begin{pmatrix} \; - \, 5 \; \\ \; - \, 2 \; \end{pmatrix}$ .

Multiply the $\textbf{x}$ component by the scalar.

Multiply the scalar number by the top number.

$4\times - \, 5=- \, 20$

Multiply the $\textbf{y}$ component by the scalar.

Multiply the scalar number by the bottom number.

$4\times- \, 2=- \, 8$

Write the resultant vector.

Write the two answers as a column vector.

4 \begin{pmatrix} \; - \, 5 \; \\ \; - \, 2 \; \end{pmatrix} = \begin{pmatrix} \; 4 \times - \, 5 \; \\ \; 4 \times - \, 2 \; \end{pmatrix} = \begin{pmatrix} \; - \, 20 \; \\ \; - \, 8 \; \end{pmatrix}

Example 6: vector multiplication, negative scalar

Solve $- \, 3 \begin{pmatrix} \; - \, 2 \; \\ \; 5 \; \end{pmatrix}$ .

Multiply the $\textbf{x}$ component by the scalar.

Multiply the scalar number by the top number.

$- \, 3\times- \, 2=6$

Multiply the $\textbf{y}$ component by the scalar.

Multiply the scalar number by the bottom number.

$- \, 3\times5=- \, 15$

Write the resultant vector.

Write the two answers as a column vector.

$- \, 3 \begin{pmatrix} \; - \, 2 \; \\ \; 5 \; \end{pmatrix} = \begin{pmatrix} \; - \, 3 \times - \, 2 \; \\ \; - \, 3 \times 5 \; \end{pmatrix} = \begin{pmatrix} \; 6 \; \\ \; - \, 15 \; \end{pmatrix}$

Example 7: vector multiplication, algebraic

Solve $3 \begin{pmatrix} \; x \; \\ \; - \, y \; \end{pmatrix}$ .

Multiply the $\textbf{x}$ component by the scalar.

Multiply the scalar number by the top number.

$3\times{x}=3x$

Multiply the $\textbf{y}$ component by the scalar.

Multiply the scalar number by the bottom number.

$3\times{- \, y}=- \, 3y$

Write the resultant vector.

Write the two answers as a column vector.

$3 \begin{pmatrix} \; x \; \\ \; - \, y \; \end{pmatrix} = \begin{pmatrix} \; x \times 3 \; \\ \; - \, y \times 3 \; \end{pmatrix} = \begin{pmatrix} \; 3x \; \\ \; - \, 3y \; \end{pmatrix}$

Teaching tips for vector multiplication

Emphasize that every component of the vector must be multiplied by the scalar quantity. Reinforce this by asking students to walk through the multiplication of vectors step-by-step.

Use scale models (for example, maps, building models) to show how scalar multiplication works by changing size while preserving proportions.

After performing scalar multiplication, ask students to describe how the new vector compares to the original. How has the magnitude changed? What happened to the direction?

Easy mistakes to make

Not multiplying both components by the scalar number
Both the $x$ component and the $y$ component need to be multiplied by the scalar number.

Writing column vectors incorrectly
Column vectors have the top number and the bottom number in the brackets. There is no need for any other punctuation marks such as commas or semicolons. There is no need for a line to separate the numbers.

Component form of a vector
Subtracting vectors
Magnitude of a vector
Vector practice problems

Practice vector multiplication questions

\begin{pmatrix} \; 5 \; \\ \; 7 \; \end{pmatrix}

\begin{pmatrix} \; 6 \; \\ \; 4 \; \end{pmatrix}

\begin{pmatrix} \; 12 \; \\ \; 6 \; \end{pmatrix}

\begin{pmatrix} \; 6 \; \\ \; 12 \; \end{pmatrix}

3\textbf{a} = 3 \begin{pmatrix} \; 2 \; \\ \; 4 \; \end{pmatrix} = \begin{pmatrix} \; 3 \times 2 \; \\ \; 3 \times 4 \; \end{pmatrix} = \begin{pmatrix} \; 6 \; \\ \; 12 \; \end{pmatrix}

\begin{pmatrix} \; 6 \; \\ \; 8 \; \end{pmatrix}

\begin{pmatrix} \; 5 \; \\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; 5 \; \\ \; 15 \; \end{pmatrix}

\begin{pmatrix} \; 6 \; \\ \; 15 \; \end{pmatrix}

5\textbf{b} = 5 \begin{pmatrix} \; 1 \; \\ \; 3 \; \end{pmatrix} = \begin{pmatrix} \; 5 \times 1 \; \\ \; 5 \times 3 \; \end{pmatrix} = \begin{pmatrix} \; 5 \; \\ \; 15 \; \end{pmatrix}

\begin{pmatrix} \; 21 \; \\ \; 31 \; \end{pmatrix}

\begin{pmatrix} \; 20.1 \; \\ \; 30.1 \; \end{pmatrix}

\begin{pmatrix} \; 2 \; \\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; 20 \; \\ \; 3 \; \end{pmatrix}

0.1\textbf{c} = 0.1 \begin{pmatrix} \; 20 \; \\ \; 30 \; \end{pmatrix} = \begin{pmatrix} \; 0.1 \times 20 \; \\ \; 0.1 \times 30 \; \end{pmatrix} = \begin{pmatrix} \; 2 \; \\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; – \, 4 \; \\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; – \, 4 \; \\ \; 6 \; \end{pmatrix}

\begin{pmatrix} \; – \, 2 \; \\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; – \, 10 \; \\ \; 6 \; \end{pmatrix}

\cfrac{2}{5} \, \textbf{a} = \cfrac{2}{5} \begin{pmatrix} \; – \, 10 \; \\ \; 15 \; \end{pmatrix} = \begin{pmatrix} \; \cfrac{2}{5} \times – \, 10 \; \\ \; \cfrac{2}{5} \times 15 \; \end{pmatrix} = \begin{pmatrix} \; – \, 4 \; \\ \; 6 \; \end{pmatrix}

\begin{pmatrix} \; 12 \; \\ \; 18 \; \end{pmatrix}

\begin{pmatrix} \; 4 \; \\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; – \, 12 \; \\ \; – \, 18 \; \end{pmatrix}

\begin{pmatrix} \; – \, 4 \; \\ \; – \, 3 \; \end{pmatrix}

6\textbf{d} = 6 \begin{pmatrix} \; – \, 2 \; \\ \; – \, 3 \; \end{pmatrix} = \begin{pmatrix} \; 6 \times – \, 2 \; \\ \; 6 \times – \, 3 \; \end{pmatrix} = \begin{pmatrix} \; – \, 12 \; \\ \; – \, 18 \; \end{pmatrix}

\begin{pmatrix} \; – \, 15 \; \\ \; – \, 12 \; \end{pmatrix}

\begin{pmatrix} \; – \, 2 \; \\ \; – \, 1 \; \end{pmatrix}

\begin{pmatrix} \; 15 \; \\ \; 12 \; \end{pmatrix}

\begin{pmatrix} \; – 15 \; \\ \; – \, 4 \; \end{pmatrix}

– \, 3\textbf{f} = – \, 3 \begin{pmatrix} \; – \, 5 \; \\ \; – \, 4 \; \end{pmatrix} = \begin{pmatrix} \; – \, 3 \times – \, 5 \; \\ \; – \, 3 \times – \, 4 \; \end{pmatrix} = \begin{pmatrix} \;  15 \; \\ \; 12 \; \end{pmatrix}

\begin{pmatrix} \; 22b \; \\ \; 27c \; \end{pmatrix}

\begin{pmatrix} \; 4b \; \\ \; 7c \; \end{pmatrix}

\begin{pmatrix} \; 4b \; \\ \; 9c \; \end{pmatrix}

\begin{pmatrix} \; 4b \; \\ \; 14c \; \end{pmatrix}

2\textbf{g} = 2 \begin{pmatrix} \; 2b \; \\ \; 7c \; \end{pmatrix} = \begin{pmatrix} \; 2 \times 2b \; \\ \; 2 \times 7c \; \end{pmatrix} = \begin{pmatrix} \; 4b \; \\ \; 14c \; \end{pmatrix}

Vector multiplication FAQs

What is vector multiplication by a scalar?

Vector multiplication by a scalar involves multiplying each component of a vector by the scalar value. This operation changes the magnitude of the vector, but the direction remains the same if the scalar is positive. If the scalar is negative, the direction of the vector is reversed.

Can you multiply two vectors together the same way as a vector and a scalar?

No, multiplying two vectors together requires different operations, such as the dot product or cross product of two vectors, depending on the context. Vector-scalar multiplication is simpler because it only involves scaling the vector by a single number (scalar).

How is vector multiplication related to trigonometry?

Vector multiplication by a scalar is not directly related to trigonometry because it doesn’t involve angles. However, vector multiplication is related to trigonometry through operations like the dot product and cross product, which both involve angles between vectors.

The dot product uses the cosine of the angle to measure alignment, while the cross product uses the sine of the angle to determine the perpendicular vector’s magnitude.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.