24 Ratio Word Problems for Grades 6-7 With Tips On Supporting Students’ Progress

Ratio word problems are introduced for the first time in 6th grade. The earliest mention of ‘Ratio’ is in the 6th grade Ratio and Proportional Relationships strand of the Common Core State Standards for math. 

At this early stage, it is essential to concentrate on the language and vocabulary of ratio relationships. Children need to be clear on the meaning of the ratio symbol right from the start of the topic. Word problems really help children understand this concept since they make it much more relevant and meaningful than a ratio question with no context.

Concrete resources and visual representations are key to the success of children’s early understanding of ratio. These resources are often used in 2nd grade word problems, 3rd grade word problems and 4th grade word problems. There is often a misconception amongst upper elementary teachers and students, that mathematical manipulatives are only for children who struggle in math. However, all students should be introduced to this new concept through resources, such as two-sided counters and visual representations, such as bar models as this can help with understanding basic mathematical concepts such as addition and subtraction word problems.

As students progress across grades, they continue to build on their knowledge and understanding of ratio. This means that students gradually move away from the practical and visual resources, while word problems continue to be a key element to any lessons involving ratios. This foundational ratio knowledge is used as a base for proportional relationships and then linear relationships in later grades. 

Ratio word problems are also an essential component of any lessons on ratio, to help children understand how ratios are used in real life. 

Ratio word problems 

Why are word problems important for children’s understanding of ratio?

Solving word problems is important for helping children develop their understanding of ratio and the different ways ratio is used in everyday life. Without this context, ratio can be quite an abstract concept, which children find difficult to understand. Word problems bring ratios to life and enable students to see how they will make use of this skill outside the classroom.

Third Space Learning’s online one-on-one tutoring programs relate math concepts to real-world situations to deepen conceptual understanding. The online lessons are personalized to fill the gaps in each individual student’s math knowledge, helping them to build skills and confidence.

How to teach ratio word problem-solving in middle school 

It is important that children learn the skills needed to solve ratio word problems. As with any math problem, children need to make sure they have read the questions carefully and thought about exactly what is being asked and whether they have fully understood this. The next step is to identify what they will need to do to solve the problem and whether there are any concrete resources or visual representations that will help them. Even older students can benefit from drawing a quick sketch to understand what a problem is asking.

Here is an example:

Jamie has a bag of red and yellow candies.

For every red candy, there are 2 yellow candies.

If the bag has 6 red candies, how many candies are in the whole bag?

How to solve:

What do you already know?

• We know that for every red candy, there are 2 yellow candies.
• If there are 6 red candies, we need to find how many yellow candies there must be. 
• If there are 2 yellow candies for each 1 red candy, then we can multiply 2 by 6, to calculate how many yellow candies there are with 6 red candies.
• Once we have calculated the total number of yellow candies (12), we then need to add this to the 6 red candies, to work out how many candies are in the bag altogether.
• If there are 6 red candies and 12 yellow candies, there must be 18 candies in the bag altogether.

 How can this be represented visually?

• We can use the two-sided counters to represent the red and yellow candies.
• We put down 1 red counter and 2 yellow counters.
• We then need to repeat this 6 times, until there are 6 red counters and 12 yellow counters.
• We can now visually see the answer to the word problem and that there are now a total of 18 counters (18 candies in the bag).

Ratio word problems for 6th grade

Word problems for 6th grade often incorporate multiple skills: a ratio word problem may also include elements from multiplication word problems, division word problems, percentage word problems and fraction word problems.

Question 1

Sophie was trying to calculate the number of students in her school.

She found the ratio of boys to girls across the school was 3:2.

If there were 120 boys in the school…

1. How many girls were there?
2. How many students were there altogether?

Answer: a) 80 b) 200

a. 80 girls

This can be shown as a bar model.

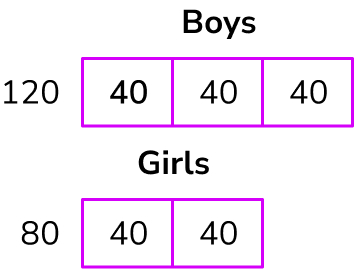
120 ÷ 3 = 40

40 x 2 = 80

b. 200 students altogether

120 boys + 80 girls = 200

Question 2

Students in the Eco Club in 6th Grade wanted to investigate how many worksheets were being printed each week in Math and English.

They found that there were 160 Math worksheets and 80 English worksheets being printed each week.

What is the ratio of Math to English worksheets? Write the ratio in simplest form.

Answer: 2:1

The ratio 160:80 can be simplified by dividing both sides by 80.

Question 3

The 6th-grade rugby club has 30 members. The ratio of boys to girls is 4:1. How many boys and girls are in the club?

Answer: 24 boys and 6 girls

The ratio of 4:1 has 5 parts:

30 ÷ 5 = 6

Boys: 4 x 6 = 24

Girls: 1 x 6 = 6

Question 4

Yasmine has a necklace with purple and blue beads.

The ratio of purple:blue beads  = 1:3

There are 24 beads on the necklace. How many purple and blue beads are there?

Answer: 6 purple beads and 18 blue beads

The ratio of 1:3 has 4 parts and 24 ÷ 4 = 6 beads per part.

Purple: 1 x 6 = 6

Blue: 3 x 6 = 18

Question 5

Maisie drives past a field of sheep and cows.

She figures out that the ratio of sheep to cows is 3:1.

If there are 5 cows in the field, how many sheep are there?

Answer: 15 sheep

If there are 5 cows in the field, the 1 has been multiplied by 5.

We need to also multiply the 3 by 5, which is 15.

Question 6

At a party, there is a choice of 2 flavors of jelly beans – orange and lemon.

The ratio of the jelly beans is 3:1 (orange: lemon).

What percent of the jelly beans are orange?

Answer: 75%

To find the percent, we need to write the ratio of orange jelly beans to total jelly beans. Since for every 3 orange jelly beans, there are 4 jelly beans in total (3 orange + 1 lemon = 4 total), the ratio is 3 to 4 or ¾. 

To convert the ratio to a percent, the denominator needs to be 100.

Multiply both parts of the fraction by 25.

75/100 is equal to 75%.

Question 7

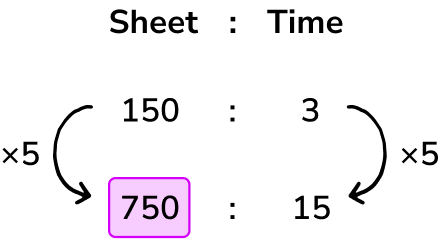
The school photocopier prints out 150 sheets in 3 minutes.

How many sheets can it print out in 15 minutes?

Answer: 750 sheets in 15 minutes

We need to multiply 3 by 5 to get 15 minutes. This means we also need to multiply 150 by 5 = 750.

Question 8

Rowen wants to buy $80 worth of books. He will have to pay a 5% tax. How much will Rowen pay in total for the books?

Answer: $84

Since $8 is 10% of $8, then half will be 5%, which is $4.

$80 + $4 = $84

Ratio word problems for 6th grade

Question 1

David has 2 grandchildren: Olivia (age 6) and Mia(age 3)

He decides to share $60 between the 2 children in a ratio of their ages.

How much does each child get?

Answer: Olivia gets $40, Mia gets $20

Ratio of 2:1 = 3 part and 60 ÷ 3 = $20 per part.

Olivia: 2 x 20 = $40

Mia: 1 x 20 = $20

Question 2

A rectangle has the ratio of width to length 2:3. If the perimeter of the rectangle is 50cm, what’s the area?

Answer: Area: 150cm2

The ratio has 5 parts:

Divide 50 by 5 to work out 1 part = 10

The 2 widths must be 2 x 10 = 20

The 2 lengths must be 3 x 10 = 30

To work out the width of 1 side, divide the 20 by 2 = 10

To work out the length of 1 side, divide the 30 by 2 = 15

Width: 10cm and Length: 15cm

Area: 10 x 15 = 150cm²

Question 3

For a class field trip, 45% of students in Kinley’s class want to go to the zoo. The other students want to go to see a play. If 11 students want to go see a play, how many total students are in Kinley’s class?

Answer: 20 students

Since 5% is 1 student, then 45% is 9 students.

Adding the students that want to go to the zoo and the students that want to see a play, is the whole class, or 100% of the students.

11 + 9 = 20 students

Question 4

A piece of ribbon is 45cm long.

It has been cut into 3 smaller pieces in a ratio of 4:5.

How long is each piece?

Answer: 20cm, 25cm

4:3:2 =9 parts: 45 ÷ 9 = 5cm per part.

4 x 5 = 20cm

3 x 5 = 25cm

Question 5

Chloe is making a smoothie for her and her 3 friends.

She has the recipe for making a smoothie for 4 people: 240ml yogurt, 120 ml milk, 2 bananas, 180g strawberries and 1 tablespoon of sugar.

1. How much yogurt would be needed to make a smoothie for 8 people.
2. How many g of strawberries are needed to make the smoothie for 2 people?

Answer:

1. 480 ml yogurt 

240ml x 2 = 480

2. 90g strawberries

180 ÷ 2 = 90

Question 6

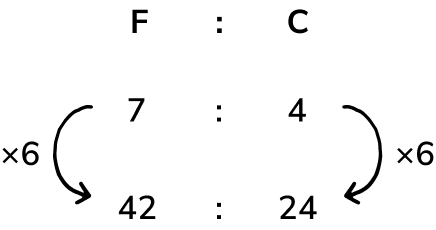
The ratio of cups of flour: cups of water in the recipe for making the dough for a pizza base is 7:4.

The pizza restaurant needs to make a large number of pizzas and is using 42 cups of flour. How much water will be needed?

Answer: 24 cups of water

Multiply 7 by 6 to get 42 cups of flour.

We, therefore, need to also multiply the 4 by 6 to calculate how many cups of water are needed.

4 x 6 = 24

Question 7

Muhammad shared $56 between him and his brother Hamza in a ratio of 3:5 (3 for Hamza and 5 for him).

How much did each get?

Answer: Muhammad got $35, his brother got $21

Ratio of 3:5 = 8 parts

56 ÷ 8 = $7 per part

3 x 7 =$ 21

5 x 7 = $35

Question 8

Scott has read 40% of his book. If he has 168 pages left, how many total pages does the book have?

Answer: 280 pages

100% – 40% = 60%

The 168 pages represent the 60% that Scott has not read.

Since 60% is 168, dividing both by 6 shows that 10% is 28. And multiplying by 10 shows how many pages are in 100% of the book.

Ratio word problems for 7th grade

Question 1

For every 250 tickets sold, the theater receives $687.50.

How much money did the theater charge for 1 ticket?

Answer: $2.75

The original ratio of tickets sold to dollars the theater made is 250 : 687.50. 

To get liters to 1, divide both sides by 250.

Question 2

A faucet drips ⅓ of a liter of water in ½ of an hour. How long does it take the faucet to drip 1 liter?

Answer: 1 and ½ hours

The original ratio of liters to hours ⅓ : ½. 

To get liters to 1, multiply by sides by 3.

When liters is 1, hours is equal to 3/2 or 1 and ½.

Question 3

The angles in a triangle are in the ratio of 3:4:5 for angles A, B and C.

Calculate the size of each angle.

Answer:

Angle A: 45°

Angle B: 60°

Angle C: 75°

3:4:5 = 12 parts.   180 ÷ 12 = 15 (each part is worth 15°)

3 x 15 = 45

4 x 15 = 60

5 x 15 = 75

Question 4

A drink is made by mixing pineapple and lemonade in the ratio of ⅔ of a cup to ⅘ of a cup. If Jayla has 1 cup of lemonade, how much pineapple should she add to keep the same drink ratio?

Answer: ⅚ of a cup

The original ratio of cups pineapple to lemonade is ⅔ :⅘.

To get cups of lemonade to 1, multiply by sides by 5/4.

When lemonade is 1 cup, pineapple is 10/12 or 5/6.

Question 5

 A $74 pair of shoes is on sale for 60% off. If Kalani buys two pairs of the shoes and pays the 7% tax on the total cost, how much money did Kalani spend in all?

Answer: $63.34

100% – 60% = 40%, so Kalani will pay 40% of the original price.

$74 0.4 = $29.60

The two pairs, before tax, cost: $29.60 + $29.60 = $59.20

Since 7% = 0.07, multiply $59.20 times 0.07 to calculate the tax.

$59.20 0.07 = $4.144 (round down to $4.14).

$59.20 + $4.14 = $63.34

*Note: You can also solve by multiplying $59.20 1.07 = $63.34

Question 6

Jaxton bought a video game console for $650 two years ago. He just sold it for $475. What is the percent decrease, to the nearest percent, in the price of the game console from when Jaxton bought it to when he sold it?

Answer: 27%

$650 – $475 = $175

Divide the difference by the original price.

$175 $650 = 0.269…

To convert the decimal to a percent, multiply by 100.

0.269 100 = 26.9%, which rounds up to 27%.

Question 7

Two companies are making an orange-colored paint.

Company A makes the orange paint by mixing red and yellow paint in a ratio of 5:7.

Company B makes the orange paint by mixing red and yellow paint in a ratio of 3:4.

Which company uses a higher proportion of red paint to make the orange?

Answer: Company B uses more red paint.

Company A: 5:7 = 5/12 is red

Company B: 3:4 = 3/7 is red

We can compare the fractions by giving them the same denominator, to find the equivalent fractions.

5/12 = 35/84

3/7 = 36/84

Question 8

$8,142 is invested in a savings account with a 0.2% simple interest rate per month. What is the total interest earned after 4 years?

Answer: $781.63

Use the equation I=Prt:

P = $8,142

r = 0.002

t = 4 years x 12 = 48 months

$8,142 (0.002 x 48) = $781.632

$781.632 rounds to $781.63

More word problems

Looking for word problems on more topics? Take a look at our practice problems for Years 3-6 including money word problems, time word problems, addition word problems and subtraction word problems.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by former UK Deputy Headteacher and has since been revised and adapted for US schools by math curriculum specialist and former elementary math teacher Katie Keeton.