Research Based Mathematics Interventions: 7 Strategies To Boost Learning

Research based mathematics interventions can help all students with math, particularly struggling students. Whether students struggle with number sense and basic facts or more challenging topics, educators have a duty to plan and adapt teaching and learning strategies accordingly. 

In this article, we dive into 8 of the most research based mathematics intervention strategies, exploring how, when, and why these need to be implemented. 

What are research based mathematics interventions?

Research based mathematics interventions are instructional learning strategies or programs designed to improve students’ mathematical skills and understanding. They are based on evidence from educational research. 

Evidence-based interventions provide additional instruction, support and resources to help students improve their understanding of math topics. 

Research based math interventions can be carried out as group tutoring but are usually taught in a small group setting or one on one. 

Math interventions are often performed during time set aside for RTI, or Response to Intervention. Response to Intervention, or RTI, is a multi-tiered system of support (MTSS) used by schools to assist all students learn and work at their grade level. The goal of RTI is to assist students in being successful and fill any educational gaps. There are 3 tiers within RTI:

• Tier 1: provides on-grade level math instruction.
• Tier 2: provides targeted interventions to students not responding to Tier 1 interventions, and would benefit from additional instruction in a small group setting. These lessons can be on grade level or below grade level. 
• Tier 3: provides intensive interventions for students not responding to Tier 1 or Tier 2 interventions. 

The research based interventions discussed in this blog apply to various stages of the RTI process and work for students at all grade levels from elementary school to middle school and high school. 

Read more: Tier 3 interventions

Why are research based mathematics interventions so important?

Research based mathematics interventions provide educators with tried and tested evidence-based strategies that effectively improve student achievement and address equity in education. 

There are plenty of math intervention myths that can impact intervention decisions. As these teaching strategies have already been proven effective, there is no guessing whether the math intervention strategy “is a good one.” This saves time when planning for small group or one-on-one instruction. 

Research based interventions are designed to address the diverse learning needs of all students in the general classroom. They target specific skills and topics students struggle with which helps close the achievement gap. 

Early implementation of research based mathematics interventions can help eliminate long-term academic struggles and lead to students having a more positive attitude when it comes to math.

Some key characteristics of research based mathematics interventions have some key characteristics, include: 

• Evidence-based design
• Targeted skills
• Differentiated instruction
• Assessment and progress monitoring
• Scaffolded instruction
• Duration and intensity

How to select which research based mathematics interventions to implement

To select the best interventions for individual students, follow a systematic approach that considers:  

• Student needs
• Research evidence
• Available resources

Assess student needs

Understand the specific needs of each students. Use student data previously collected to help identify students’ areas of strength and weakness, including:

• Standardized test scores
• Universal screening
• Classroom assessments
• Teacher observations 

This data helps educators make the best decisions for each student.

Research evidence

Look for well-researched interventions and programs that show evidence of closing learning gaps. 

The tried and tested nature of research based mathematics interventions is a huge advantage. It means educators can move forward with interventions already proven to work. 

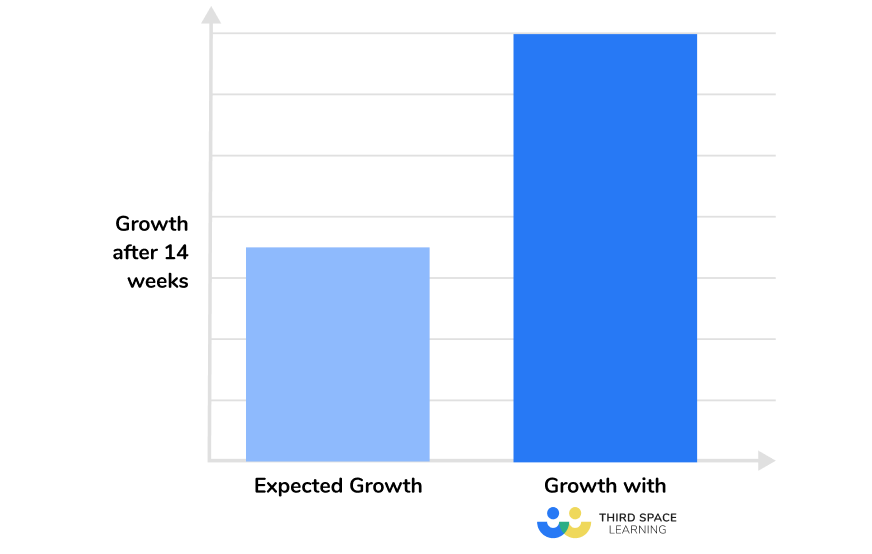
One on one math interventions with Third Space Learning’s math specialist tutors are proven to boost student achievement. Just one 45-minute session a week can boost progress by 7 months in just 14 sessions.

Available resources

It is highly unlikely that the average classroom is equipped with top-of-the-line technology. Nor do they have access to enough trained personnel. 

Before planning math interventions, evaluate what is readily available: 

• Technology
• Teacher aids
• Instructional materials

Assess the consistency of a math intervention program or summer tutoring program implementation with the resources available.  

Math intervention resources, such as the math intervention packs are readily available to download for free in the Third Space Learning resource library to help save teachers time. Each pack is taken straight from Third Space Learning’s one on one math interventions. 

All math intervention packs contain teacher or tutor notes, lesson slides and questions and prompts to ask students if they are stuck.  

Review of student needs, resources available and researched based interventions, helps schools select the best strategies for their students.

7 Research based mathematics interventions strategies

Here we look at what the different research based mathematics intervention strategies are, how to implement these math intervention strategies, when these strategies are the most effective and why you should consider trying these strategies in your classroom today.

1. Explicit instruction

What: Explicit instruction is a direct approach to teaching math. Concepts, strategies or skills are demonstrated with detailed explanations and modeling for students. This commonly takes place during the lesson plan phase for educators. 

How: Create a detailed plan of how to teach a topic to ensure students are given the explanations and modeling needed to learn a new math concept.

When: Explicit instruction happens each time math learning is taking place. It can occur in whole group instruction, small group tutoring, and one-on-one instruction.

Why: Explicit instruction is effective for students who benefit from clear and structured learning environments. These students include students with learning disabilities, special education students, English language learners and struggling learners.

2.  Visual representations

What: Visual representations are drawings or images of concepts.  They can include: 

• Diagrams
• Charts 
• Graphic organizers
• Models
• Manipulatives

These representations can help students better understand more abstract concepts, such as fractions and multiplication. Visual representations can further help students make connections to other math concepts they have learned. 

How: Visual representations can be used in many different ways. Using visual representations to introduce a new concept during whole group instruction allows all students access to the intervention. 

Visuals can be displayed within the classroom, on anchor charts, in math journals, or posted in online classrooms.

When: Using visual representations can take place at any point in a students learning journey, including whole group instruction, small group instruction and one-to-one instruction.

Teaching students to draw visual representations when learning new concepts, reviewing older concepts or during tests can help to embed learning in students long-term memory. 

Why: Using visual representations is effective for all students. Visual representations strengthen student understanding, engagement and retention of math concepts.

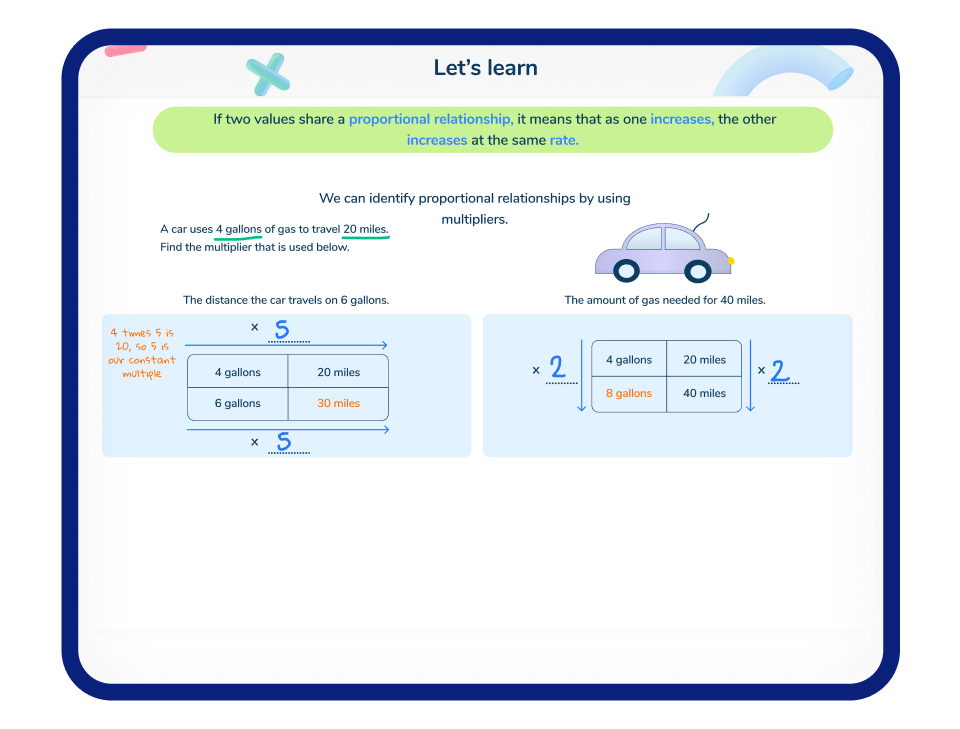
All Third Space Learning one-on-one tutoring sessions take place in an online, interactive classroom. Session slides use visual representations to help students understand abstract concepts such as proportional relationships. Tutors provide coherent explanations, alongside visuals, to match the pitch and pace of the student’s needs.

3. Peer-assisted instruction

What: Peer-assisted instruction is an alternative to teacher-lead instruction. It involves students working in pairs or small groups to learn from each other. 

To be successful, this strategy takes strategic planning and facilitating from the teacher or educator in the classroom. 

Even though the learning sessions are student-led, the teacher should continue to provide direction, structure, and intervene as needed to ensure that the learning experience is positive and beneficial.
 

How: Peer-assisted instruction takes planning from the teacher. Select student tutors that demonstrate a strong understanding of the concept they will be ‘teaching’ to the other students. 

You may decide to provide ‘training’ for these students, to help them better implement their tutoring. 

Establish the tutoring pairs or groups for these students and continue to monitor sessions to ensure that the expectations are being met and followed.

Peers should never introduce new mathematical concepts to classmates. Their role is to provide targeted support to peers on “tough to learn” concepts.

When: Peer-assisted instruction usually happens in small group settings, typically during guided learning.

Why: Peer-assisted instruction has many benefits, including: 

• Improved mastery of math concepts
• Increased self-confidence in math 
• Greater motivation
• Engagement in learning

The power of peer interaction and instruction can open a gateway to learning for students who struggle most. 

4. Problem-solving strategies 

What: Problem solving strategies are techniques students can use to solve math problems. Some of these strategies use acronyms to help students remember the steps of the strategy.

For example:

Most strategies ensure students understand or read the problem carefully, identify key information, plan a solution and check their solution for accuracy. Some may require students to draw a picture or diagram as part of the problem-solving strategy. 

How: To make an effective problem-solving strategy, determine which steps are the most important when tackling a word problem.  

Posting these steps on an anchor chart for students to view or include in their math journals helps reinforce these steps. 

When: When working on word problems with students, reinforce the learned problem-solving strategies. Model the steps to a whole group setting and then set expectations for students to use them anytime they are working in a small group or independently.  

Why: When students are equipped with a plan to tackle math word problems, they become more confident and proficient math problem solvers. Keep student expectations here consistent. 

5. Effective practice opportunities

What: Effective practice opportunities include activities and exercises that allow students to apply and practice their math knowledge and math skills meaningfully. 

While worksheets are typically seen as the “easy” way to provide multiple practice opportunities for students, they are not the most effective.

How: Plan purposeful real-world problems for students to solve that include critical thinking and use of problem-solving skills. 

Provide math games and brainteasers during guided math stations, allowing students to work as a team to solve problems. This is a great way to incorporate interactive technology tools. These tools can be effective in having students work on their fact fluency, as they get real-time feedback as they work through their math facts. 

When: Allow students to practice their newly acquired math knowledge and skills in multiple ways. Traditionally, this would take place during guided or independent practice. 

Why: When students practice their math skills in a safe and engaging way, they build confidence and have “fun” doing so! This gives students the ability to develop a deeper understanding and appreciation for the math they are learning. 

6. Metacognitive strategy instruction

What: Metacognition is the awareness and understanding of one’s own thinking. Metacognitive strategies help students understand their own thinking, particularly when it comes to math. 

Metacognitive strategies include: 

• Goal setting
• Plan and organize solving a mathematical problem 
• Develop schema
• Self-questioning
• Reflect and evaluate grades

How: Teachers should model metacognition in the classroom through instruction. For example, while solving a word problem, model thinking through your plan to solve the question. Stop and ask questions aloud, so students can better grasp how to self-question. Talk students through setting goals before quizzes or exams and allow them time to reflect and evaluate their progress. This is all a part of metacognitive strategy instruction.

When: Model metacognitive strategies during all instruction so students do these things as well. As the facilitator of learning prompt students to verbalize their plan for a word problem or to say their questions aloud in small group settings. 

Why: Metacognitive strategies in the classroom empower students to become more independent and prepare them to tackle complex math concepts and overcome obstacles that they will likely face during their K-12 mathematics instruction.

7. Formative assessment

What: Formative assessment is the continuous process of progress monitoring, assessing understanding and providing feedback to support student learning. 

Formative instruction uses assessments as a tool to drive instruction and make data-driven decisions.

How: Often, the term assessment is associated with a formal sit down, with a pencil and paper to collect a grade. Formative assessment is more than a pen to paper exam. 

Formative assessment such as warm-up questions check understanding from the previous lesson. 

Alternatively, use exit tickets at the end of whole group teaching to gauge student understanding of the current lesson. 

Formative assessment is a great strategy to collect data on concepts that students need prerequisite knowledge from a previous grade level. For example, display a 4th grade multiplication question for 5th graders to identify students who need a little more practice before tackling the standard algorithm. 

All Third Space Learning one-on-one math tutoring sessions use a range of formative assessment strategies to assess students understanding of the taught math concepts. Students complete post-session questions to check student understanding and allow tutors to prepare concepts for the next session.  

When: Formative instruction can be completed at different points of instruction. If students answer a quick question (think 1-3 minutes), then there should be time to collect formative data. 

Why: Teachers who properly utilize formative instruction and assessment within their classrooms can properly intervene when they have a struggling student. 

Through continuous progress monitoring, educators are constantly aware of which students are struggling. 

Formative instruction allows teachers to use the data collected to drive instruction within the classroom. For example, if a handful of students struggling with adding decimals, create a small group to immediately support students.

8. One-on-one tutoring

What: One-on-one tutoring is personalized instruction from one tutor to one student. The tutor works closely with the student and teacher to address specific gaps and provide individualized support for the one student. One-on-one tutoring is a highly effective intervention strategy, particularly high-dosage tutoring. 

How: Formative and summative data inform an individualized instruction plan for each student. Tutors then provide targeted support to the student according to their learning gaps. Personalized feedback in real-time accelerates math learning for each student.  

When: One-on-one math tutoring should not take place when the rest of the class is learning a new concept. This can cause them to fall further behind. Ideally, it should take place before or after school, or during planned intervention periods. Sessions can be scheduled as needed, and as much as the student needs.

Why: For many reasons one-on-one tutoring is highly effective. Besides the personalized instruction each student receives, the tutor can build trust and rapport with the student they are tutoring. 

One-on-one tutoring allows flexibility in scheduling as there is one student’s schedule to work around, not a small group of them. 

Tutors can closely monitor student progress through one-on-one tutoring and make any changes in real-time. 

Third Space Learning offers flexible math tutoring schedules. Sessions can take place before, during and after school to fit your schedule. Schools can pick the session length to suit students and change timeslots, students, dosage and frequency at any point in the school year. 

How to review the success of research based mathematics interventions

Once research based math interventions are implemented, educators and schools must assess their effectiveness. 

Before any math intervention begins, establish the goals or objectives of the intervention and make them SMART – specific, measurable, achievable, relevant, and time-bound.

Collect data during interventions to progress monitor student learning towards the goal or objective set at the beginning. Once the implementation is complete, student achievement needs to be measured. This can be done through summative assessment, student surveys and observations. 

A review of the data collected throughout the intervention period helps to determine the overall effectiveness of the interventions performed. 

This helps educators make data-informed decisions and adjustments to all aspects of math instruction to ensure student success. 

Conclusion

Research based math interventions provide educators with strategies to increase student learning within the math classroom and assist struggling students. Preparation, implementation, and assessment of the effectiveness of each classroom intervention is crucial. 

Educators must empower themselves to continue to make data-driven decisions that are best suited for their students. Whether interventions take place during whole group instruction or in a one-on-one situation, feel confident that when delivered with fidelity, student learning will accelerate and reduce math anxiety. 

Research based mathematics interventions FAQs

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?