Negative Exponents - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Square root

Cube root

Scientific notation

Order of operations

Negative numbers

Math resources Number and quantity Exponents

Negative exponents

Here you will learn about negative exponents, including what they are, how to simplify and evaluate them, and how to combine them with other laws of exponents.

Students will first learn about negative exponents as a part of expressions and equations in grade $8,$ and will continue to build on this knowledge in high school.

What are negative exponents?

Negative exponents are a type of index, written with a negative sign, that represents a number that can be written as a fraction.

For example,

3^{-2}=\cfrac{1}{3^{2}}=\cfrac{1}{9}

A negative exponent does not mean that the base is a negative number.

A negative exponent means if the base is a positive number, the denominator of the fraction remains positive.

Let’s see why a negative exponent is a fraction using the powers of $10\text{:}$

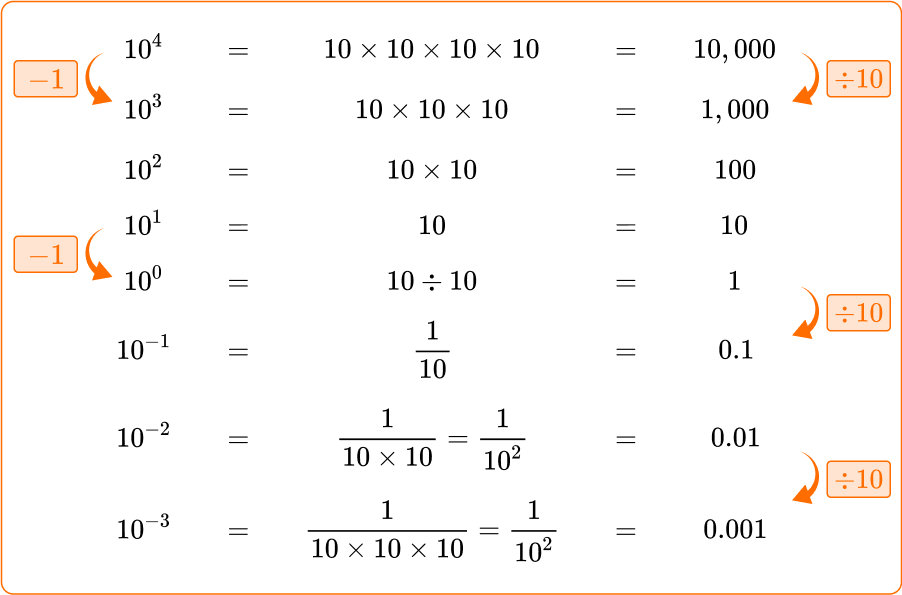
As each row is divided by $10,$ the power is reduced by $1.$

When you reach $10^0$ (the zero exponent) you are dividing the base number by itself, so any base to the power of $\bf{0}$ is always equal to $\bf{1}.$

When you divide by a further $10,$ you get $0.1=\cfrac{1}{10}=10^{-1}.$

As you continue to divide by $10,$ the denominator of the fraction becomes increasingly large, meaning that the original number gets smaller and smaller $($ closer to $0).$

Positive reciprocal

Another term for the negative power is the positive reciprocal.

The reciprocal of a number is the value that can be multiplied by the original number to get the answer of $1.$

For example,

$2\times\cfrac{1}{2}=1$ , and so $\cfrac{1}{2}$ is the positive reciprocal of $2.$

Introducing a negative exponent, we get $2^{-1}=\cfrac{1}{2^{1}}=\cfrac{1}{2}$ which can be expressed in a general form as:

$x^{-a}=\cfrac{1}{x^{a}}$

where $x$ and $a$ are constants.

Most of the laws of indices can include a negative exponent and the toughest questions usually involve a fractional base number raised to a negative fraction.

For example,

$\left(\cfrac{25}{4}\right)^{-\frac{3}{2}}=\cfrac{8}{125}$

Simplify and evaluate

Questions will often require you to simplify or evaluate an expression.

These terms are subtly different and so the table below shows a couple of examples of the difference between them:

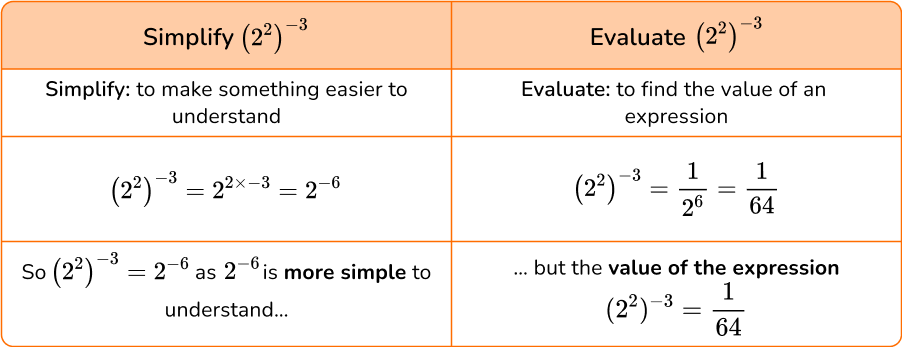
Remember: a fraction can also be converted to a decimal.

What are negative exponents?

Common Core State Standards

How does this relate to $8$ th grade math?

Grade 8: Expressions and Equations (8.EE.A.1)
Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, $3^{2}\times3^{-5}=3^{2+-5}=3^{2-5}=3^{-3}=\cfrac{1}{3^3}=\cfrac{1}{27}$

[FREE] Negative Exponents Worksheet (Grade 8)

Use this worksheet to check your grade 8 students’ understanding of negative exponents. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Negative Exponents Worksheet (Grade 8)

Use this worksheet to check your grade 8 students’ understanding of negative exponents. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

How to solve with negative exponents

In order to use negative exponents:

Simplify any powers using laws of indices.
Evaluate or solve (if required).

Negative exponents examples

Example 1: simplify and evaluate

Simplify and evaluate the expression $6^{-2} \div 6^{-4}.$

Simplify any powers using laws of indices.

As $x^{a}\div{x}^{b}=x^{a-b},$ you have:

6^{-2}\div6^{-4}=6^{-2--4}=6^{-2+4}=6^2

2Evaluate or solve (if required).

Evaluating the expression $6^2,$ you get:

6^2=6\times6=36.

So, $6^{-2}\div6^{-4}=36.$

Example 2: algebraic terms

Write the following expression as a fraction in its simplest form: $2y^{-a}\times2x^{b}.$

Simplify any powers using laws of indices.

The bases are different for each term in the expression, so treat each term separately:

$2y^{-a}=2\times{y^{-a}}=2\times{\cfrac{1}{y^{a}}}=\cfrac{2}{y^a}$

$2x^{b}$ does not require any simplifying at this stage.

Now multiply these terms together:

$2y^{-a}\times{2x^{b}}=\cfrac{2}{y^a}\times2x^b=\cfrac{2\times2x^b}{y^a}=\cfrac{4x^b}{y^a}$

Evaluate or solve (if required).

As this is an algebraic expression with no values for $x, y, a,$ or $b,$ we cannot evaluate this expression.

The solution is therefore: $2y^{-a}\times{2x^{b}}=\cfrac{4x^{b}}{y^{a}}$

Example 3: inequalities with coefficients

Solve the inequality $(3x)^{-2}<\cfrac{1}{36}.$

Simplify any powers using laws of indices.

Looking at the left hand side of the inequality sign, $3x$ is being raised to the power of $-2$ and can be written as,

$(3x)^{-2}=\cfrac{1}{(3x)^{2}}=\cfrac{1}{3^{2}x^{2}}=\cfrac{1}{9x^{2}}$

So you now have the inequality,

$\cfrac{1}{9x^{2}}<\cfrac{1}{36}$

Evaluate or solve (if required).

Multiplying both sides by $9x^2,$ you get

$1<\cfrac{9x^{2}}{36}$

which can be simplified by dividing the numerator and the denominator by $9,$

$1<\cfrac{x^{2}}{4}$

Multiplying each side by $4,$ you get

$4<x^2.$

Which is the same as

$x^2>4.$

Calculating the square root of both sides of the inequality symbol, you obtain the solutions:

$x<-2$ and $x>2.$

Remember: $-2 \times -2=4$ and so any value less than $-2$ will be larger than $4 (-3 \times -3=9, -10 \times -10=100$ etc $).$ This is the same as for any value larger than $2.$

Example 4: negative fractional power

Simplify and evaluate the following expression: $125^{-\frac{2}{3}}$

Simplify any powers using laws of indices.

As the exponent of $125$ is a fraction, and a negative number, we are going to simplify the base by looking at the denominator of the power first. As the denominator of the fraction is the nth root of the base number.

$125^{-\frac{2}{3}}=\left(125^{\frac{1}{3}}\right)^{-2}=\left(\sqrt[3]{125}\right)^{-2}=5^{-2}$

Remember, raising a term to the power of $\cfrac{1}{3}$ is exactly the same as the cube root.

Now look at the negative aspect of the power,

$5^{-2}=\cfrac{1}{5^{2}}$

Evaluate or solve (if required).

The expression $\cfrac{1}{5^{2}}$ is the simplified form of the expression, but you can now evaluate the expression as you know that $5^{2}=25$ so,

$\cfrac{1}{5^{2}}=\cfrac{1}{25}$

So the solution is $\cfrac{1}{25}.$

Example 5: fractional base number

Evaluate: $\left(\cfrac{3}{4}\right)^{-3}$

Write your answer as a mixed number.

Simplify any powers using laws of indices.

Starting with a base of $\cfrac{3}{4}$ that is raised to the power of $-3,$ you know that the negative power produces the positive reciprocal of the base $($ the reciprocal is the number you multiply by to get the answer $1).$

So what can you multiply $\cfrac{3}{4}$ by, to get the value of $1?$

$1\div{\cfrac{3}{4}}=1\times{\cfrac{4}{3}}=\cfrac{4}{3}$

So as $\cfrac{3}{4}\times{\cfrac{4}{3}}=\cfrac{12}{12}=12\div{12}=1,$ the reciprocal of $\cfrac{3}{4}$ is $\cfrac{4}{3}.$

So you can now say,

$\left(\cfrac{3}{4}\right)^{-3}=\left(\cfrac{4}{3}\right)^{3}=\cfrac{4^{3}}{3^{3}}.$

Evaluate or solve (if required).

Looking at the power of the numerator and denominators separately, you have

\begin{aligned} 4^3&=4\times4\times4=64\\\\ 3^3&=3\times3\times3=27 \end{aligned}

and so $\cfrac{4^{3}}{3^{3}}=\cfrac{64}{27}=2\cfrac{10}{27}.$

Example 6: expressing a power with a different base

Simplify fully $(4^{-10})^{\frac{1}{2}}.$ Write your answer as a power of $2.$

Simplify any powers using laws of indices.

The law of indices you are going to use involves parentheses, namely: $\left(x^{a}\right)^{b}=x^{a\times{b}},$ which leaves you with

$\left(4^{-10}\right)^{\frac{1}{2}}=4^{-10\times{\frac{1}{2}}}=4^{-5}$

$4^{-5}=\cfrac{1}{4^{5}}.$

Evaluate or solve (if required).

The question does not want you to state the value of $\cfrac{1}{4^{5}}.$ Instead, the question asks for the solution to be written as a power of $2,$ so change the expression so that the base number is $2,$ instead of $4.$

As $4=2^{2},$ you have $\cfrac{1}{4^{5}}=\cfrac{1}{\left(2^{2}\right)^{5}}=\cfrac{1}{2^{2\times{5}}}=\cfrac{1}{2^{10}}$

So the solution is $\cfrac{1}{2^{10}}.$

Teaching tips for negative exponents

Make sure that students have a clear definition of what negative exponents are, including examples of negative exponents and rules to follow in order to solve them.

Introduce students to the concept using visual aids, such as diagrams and manipulatives, before giving students worksheets with practice problems that increase in rigor as they become more comfortable with the concepts.

Teach students the properties of exponents (rules of exponents), including the product rule $a^m \times a^n=a^{m+n}$ and quotient rule $\cfrac{a^m}{a^n}=a^{m-n},$ and explain how these rules apply to expressions with negative exponents.

Easy mistakes to make

Negative powers and negative number
A common error is to think that a negative power suggests that the entire number is a negative number. This is incorrect because a negative power means that you are finding a positive reciprocal of the base.
For example, $2^{-4}=-2^4=-16$ is incorrect. The correct answer is $2^{-4}=\cfrac{1}{2^{4}}=\cfrac{1}{16}.$

Changing the base incorrectly
For example, $5^{3}\times2^{-4}=(5\times{2})^{3-4}=10^{-1}=\cfrac{1}{10}.$

This is incorrect as the bases must be the same when simplifying calculations with powers.
The correct answer would be $5^{3}\times{2^{-4}}=5^{3}\times{\cfrac{1}{16}}=\cfrac{125}{16}.$

Subtracting a negative number
A common error is to incorrectly subtract negative numbers.
For example, $3^{-2}\div{3^{-5}}=3^{-2-5}=3^{-7}=\cfrac{1}{3^{7}}.$

This is incorrect because the $5$ is a negative number, and subtracting a negative number means that you add.
The correct answer would be $3^{-2}\div3^{-5}=3^{-2--5}=3^{-2+5}=3^3=27.$

PEMDAS
When raising a base to a power, the power is associated with a variable or an expression.
For example, let’s look at $3x^{-2}.$ Using PEMDAS you can see that, $x$ is being raised to the power of $-2,$ and then is multiplied by $3$ to get the answer $\cfrac{3}{x^{2}}.$

However a common error is to calculate $3x$ raised to the power of $-2,$ giving the answer $\cfrac{1}{9x^{2}}$ which is incorrect.

If this was the case, the question would be written as $(3x)^{-2}.$

Incorrect application of the exponent
A similar circumstance is applied to fractions that are raised to a power.
For example, let’s look at $\left(\cfrac{5}{2}\right)^{-3}.$ The correct application of the laws of indices would give a correct answer of $\left(\cfrac{5}{2}\right)^{-3}=\left(\cfrac{2}{5}\right)^{3}=\cfrac{8}{125}.$

However a common error would be to apply the $-3$ only to the numerator, leaving the denominator unchanged.
This would give the incorrect answer of $\left(\cfrac{5}{2}\right)^{-3}=\cfrac{1}{125}\times\cfrac{1}{2}=\cfrac{1}{250}.$

Powers of $10$
Radicals

Practice negative exponents questions

25

-25

-\cfrac{1}{25}

\cfrac{1}{25}

5^{4}\times{5^{-6}}=5^{4-6}=5^{-2}=\cfrac{1}{5^{2}}=\cfrac{1}{25}

\cfrac{x^{a}}{y^{b}}

\cfrac{x^{a}}{2y^{b}}

\cfrac{x^{a}y^{b}}{2}

\cfrac{2}{x^{a}y^{b}}

3x^{a}\div{6y^{-b}}=3x^{a}\div\cfrac{6}{y^{b}}

=3x^{a}\times{\cfrac{y^{b}}{6}}=\cfrac{3x^{a}y^{b}}{6}=\cfrac{x^{a}y^{b}}{2}

-4<x<4

x<4

-\cfrac{1}{4}<x<\cfrac{1}{4}

x>4, x<-4

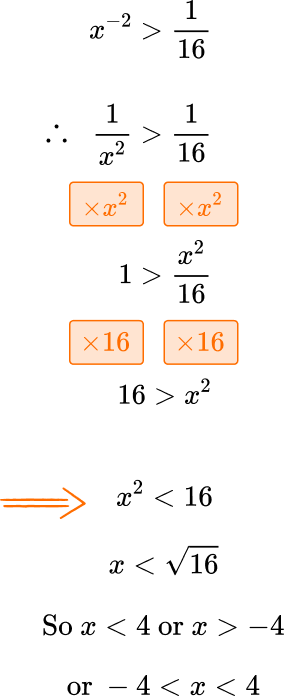
Negative exponents 3 US

\cfrac{1}{64}

-12

\cfrac{1}{8}

-64

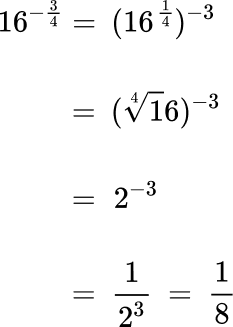
Negative exponents 4 US

\cfrac{1}{25}

\cfrac{-2}{5}

25

-\cfrac{1}{5}

\left(\cfrac{1}{5}\right)^{-2}=\left(\cfrac{5}{1}\right)^{2}=5^{2}=25

2^2

2^{-2}

2^{-1}

2^{\frac{-2}{3}}

\left(8^{2}\right)^{-\frac{1}{3}}=\left(2^{3\times{2}}\right)^{-\frac{1}{3}}=\left(2^{6}\right)^{-\frac{1}{3}}=2^{-\frac{6}{3}}=2^{-2}

Negative exponents FAQs

What is the negative exponent rule?

The negative exponent power rule states that when a number or variable with a negative exponent is used, it represents the reciprocal of the same number or variable, represented by $a^{-n}=\cfrac{1}{a^n},$ where $a$ is a non-zero real-number or variable and $n$ is a positive integer.

What is the difference between positive exponents and negative exponents?

Positive exponents represent exponential growth, while negative exponents represent exponential decay. They represent inverse operations, multiplication and division respectively, and have different effects on the value of the expression they are applied to.

What is the rule for multiplying negative exponents?

The rule for multiplying expressions with negative exponents includes combining exponents by addition and then simplifying the expression.

Can you have a negative fractional exponent?

Yes, negative fractional exponents exist in the world of mathematics. With a negative fractional exponent, you would take the reciprocal of the base raised to the absolute value of the exponent. For example, $x^{-\frac{1}{2}}=\cfrac{1}{\sqrt{x}}.$

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.